2.3.2. Вывод дифференциального уравнения неустановившейся фильтрации однородного флюида по закону Дарси. Функция л. С. Лейбензона.

Для вывода дифференциального уравнения неустановившейся фильтрации используем уравнение неразрывности

или

Это уравнение справедливо только в том случае, если внутри объема нет источников или стоков, выделяющих или поглощающих флюид, не происходит химических реакций, фазовых превращений и т.д.

Дальнейшее преобразование связано с введением функцию (функции Лейбензона),

или или Р = const (2.16)

Равенство (2.16) позволяет определить явный вид функции Лейбензона при заданном уравнении состояния

Математическая модель фильтрации сжимаемой жидкости (газа) в недеформируемой изотропной пористой среде, без учета силы тяжести будет:

^, , (2.14)

После введения функции Лейбензона систему (2.14) можно представить в виде

^, , ^, (2.15)

Замкнутые системы (2.14) и (2.15) представляют математическая модель фильтрации вязкой сжимаемой жидкости (газа) в недеформируемой изотропной пористой среде. Описывают неустановившееся фильтрационное течение.

Для установившегося процесса системы упрощаются

^, , (2.16)

и , , ^, (2.17)

При установившейся фильтрации первое уравнение системы (2.17) представляется уравнением Лапласа для функции Лейбензона, интегрируя которое можно найти функцию Лейбензона и затем определить распределение скорости и давление в пласте.

Первое уравнение системы (2.15) содержит две неизвестные функции - плотность и функцию Лейбензона, но при задании уравнений состояния (последнее уравнение в системе) его можно представить в виде дифференциального уравнения только для функции Лейбензона.

Если пласт считается деформируемым, пористость и проницаемость полагаются функциями давления, при этом изменение давление в пласте существенно, что вязкость тоже полагается функцией давления, то подставляя закон Дарси в уравнение неразрывности, получим

(37)

тогда дифференциал функции Лейбензона равен:

,

тогда

, (2.20)

Тогда систему можно представить в виде

, ,

, проницаемость , пористость , вязкость (2.21)

2.3.2 Зависимость параметров флюидов и пористой среды от давления

Выведенные дифференциальные уравнения неразрывности и движения содержат, кроме скорости фильтрации и давления, плотность флюида ρ, коэффициент пористости m, коэффициент проницаемости k (для изотропной среды) и вязкость флюида μ. Для дальнейших расчетов надо знать зависимости этих коэффициентов от давления и температуры.

При изотермическом процессе зависимость плотности однородного флюида от давления представляет собой уравнение состояния.

При установившейся фильтрации капельной жидкости можно считать ее плотность не зависящей от давления, т. е. рассматривать жидкость как несжимаемую, тогда ρ = const.

В неустановившихся процессах часто большое количество нефти можно отобрать за счет расширения ее объема при снижении давления. В этих процессах необходим учет сжимаемости жидкости. При движении газа необходимо учитывать зависимость плотности газа от давления. Поэтому в качестве основных уравнений состояния рассматривают уравнения состояния упругой жидкости, совершенного и реального газов. В дальнейшем считаем, что давление является функцией только плотности. Процессы, в которых называются баротропными. Примером баротропных процессов могут служить изотермические фильтрационные течения.

Коэффициент объемного сжатия жидкости β_ж равен отношению относительного изменения объема жидкости к изменению давления

(2.22)

Знак «-» поставлен для того, чтобы коэффициент объемного сжатия жидкости был положительной величиной. При увеличении давления (dp >0) уменьшается (dV_ж<0) и наоборот. Коэффициент объемного сжатия считается универсальной постоянной и не зависит от температуры и давления.

В. Н. Щелкачев приводит следующие значения коэффициента объемного сжатия (Па ^-1):

для различных нефтей отечественных месторождений - 7·10^-10 - 30·10^-10;

для пластовых вод 2,7·10^-10 - 5·10^-10.

В формуле (2.22) перейдем от объемов к плотности; подставив для однородной жидкости

, ^,

Т.к. М = const, получим: ^, откуда

Проинтегрируем последнее равенство от фиксированных значений р₀ и ρ₀ до текущих значений р и ρ соответственно:

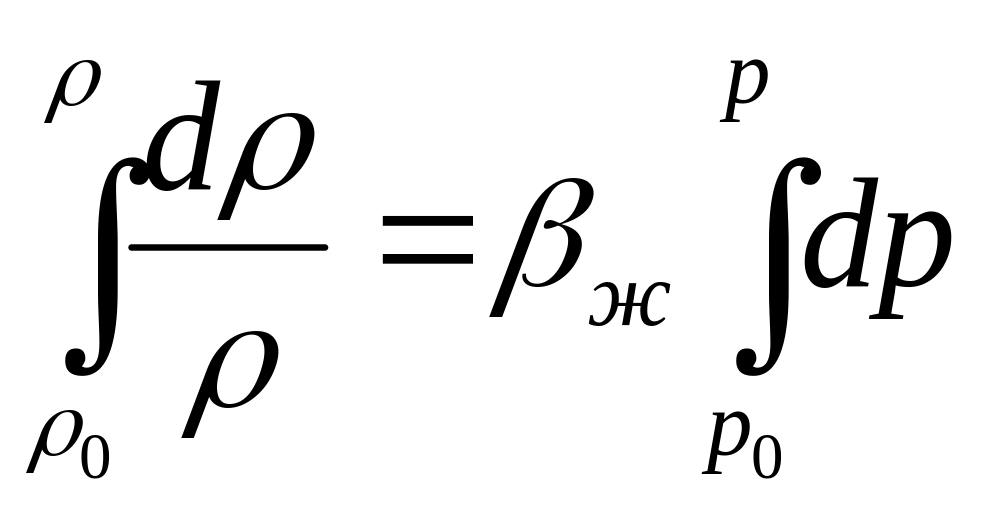и в результате получим , потенцируя, найдем

(2.23)

Показатель степени β_ж(р - p₀) обычно много меньше единицы. Поэтому принимают

При этом получаем линейную зависимость плотности упругой слабосжимаемой жидкости при небольших перепадах давления:

(2.24)

Для больших перепадов давления р - р₀ надо использовать уравнение состояния упругой жидкости в виде (2.23).

Иногда вместо коэффициента объемного сжатия вводят модуль упругости жидкости К_ж = 1/ β_ж. Формулы (2.23) и (2.24), выраженные через модуль упругости Кж, примут следующий вид:

,

Природные газы можно считать идеальными (совершенными), если пластовые давления газовых месторождений невелики (до 6-9 МПа), и газ отбирают при депрессии до I МПа. Уравнением состояния идеального газа служит уравнение Клайперона-Менделеева:

р/ρ = RT, (2.25)

где R - газовая постоянная для газа с молекулярной массой ¯μ, связанная с универсальной газовой постоянной R зависимостью .

Если Т = Т_пл = cosnt, а р_ат - плотность газа при атмосферном давлении р_ат и пластовой температуре Т_пл, то

(2.26)

Приравняв левые части соотношений (2.25) и (2.26), получим уравнение состояния идеального (совершенного) газа, которым будем пользоваться в дальнейшем:

(2.27)

В практике все чаще встречаются газовые месторождения с высокими пластовыми давлениями (до 40-60 МПа), которые иногда эксплуатируются с большими депрессиями (порядка 15-30 МПа). В этих условиях следует использовать уравнение состояния реального газа, которое, в отличие от уравнения (2.27), запишется в виде

р/ρ = zRT, (2.28)

где z - коэффициент, характеризующий степень отклонения состояния реального газа от закона идеальных газов (коэффициент сверхсжимаемости) и зависящий от давления и температуры z = z(p, Т). Значения коэффициента сверхсжимаемости z справочные данные (определяются по графикам Д. Брауна).

Для изотермической фильтрации реального газа зависимость плотности от давления принимает вид

(2.29)

Зависимость z(p) при постоянной температуре можно считать линейной при малых изменениях давления:

(2.30)

где z₀ - коэффициент сверхсжимаемости при р = р₀;

и экспоненциальной при больших изменениях давления:

(2.31)

причем константа а_z подбирается так, чтобы кривая как можно ближе подходила к соответствующей эмпирической кривой на графиках Д. Брауна.

Используя приведенные уравнения состояния можно вычислить функцию Лейбензона для каждого случая.

Для упругой жидкости с уравнением состояния (2.23):

, (2.32)

При малых значениях и уравнением состояния (2.24) равенство (2.32) будет

(2.33)

т. е. имеем тот же вид, что и для несжимаемой жидкости.

Для совершенного газа с уравнением состояния

получаем , (2.34)

т. е. функция Лейбензона пропорциональна квадрату давления.

Для реального газа с уравнением состояния (2.39)

, (2.35)

т. е. функция Лейбензона записывается в виде интеграла.