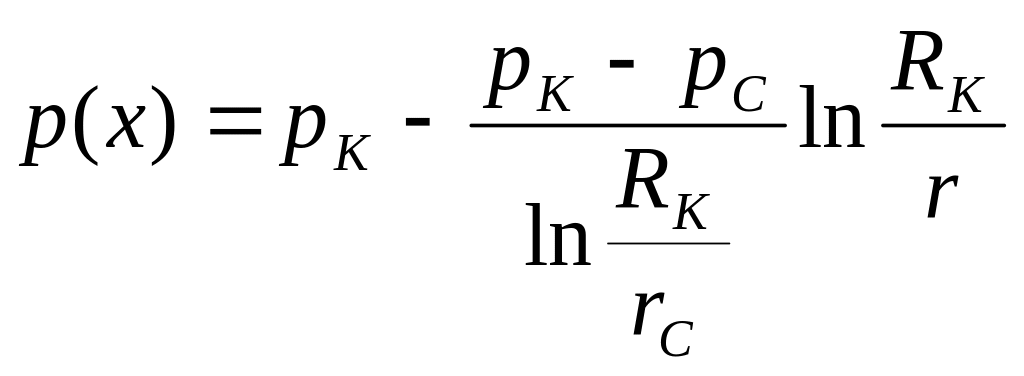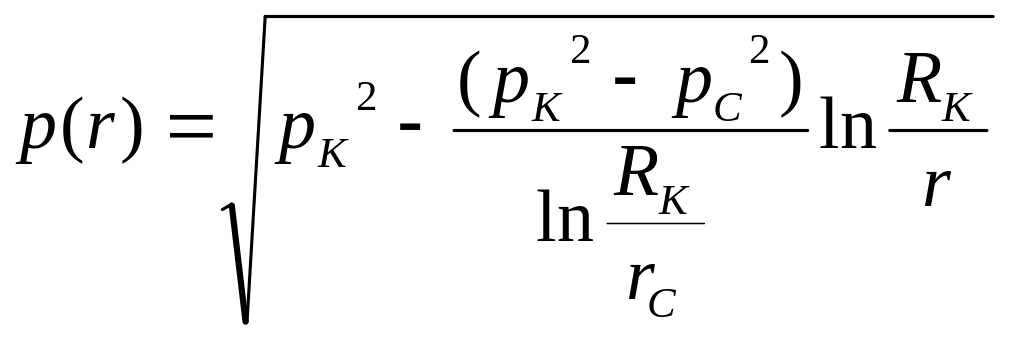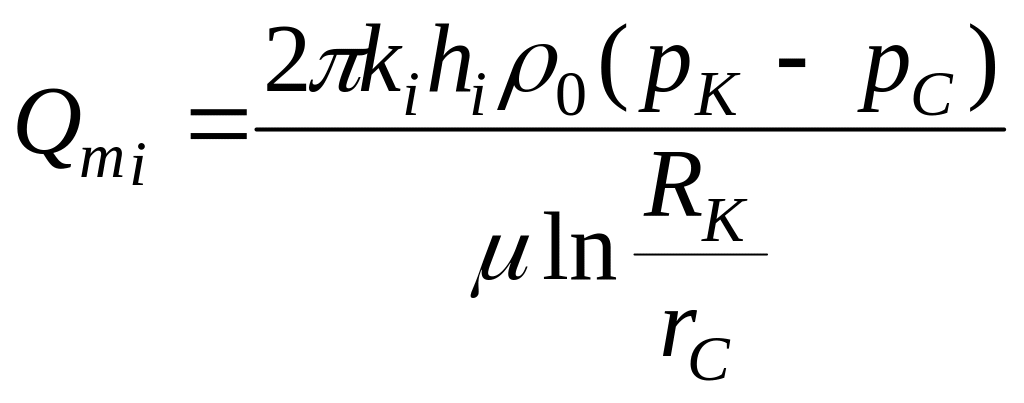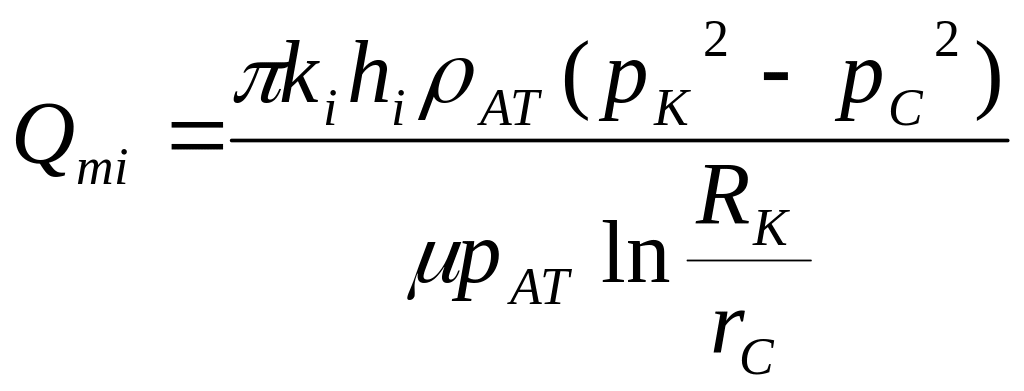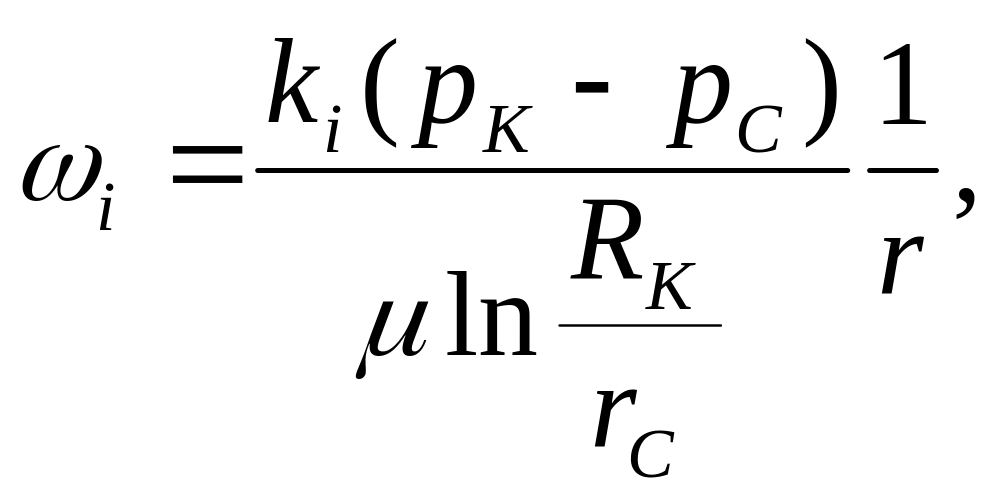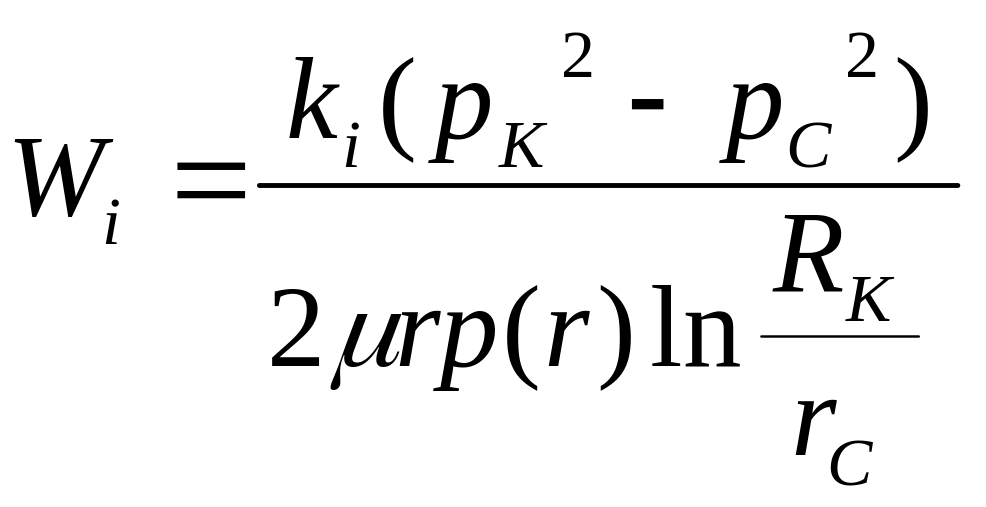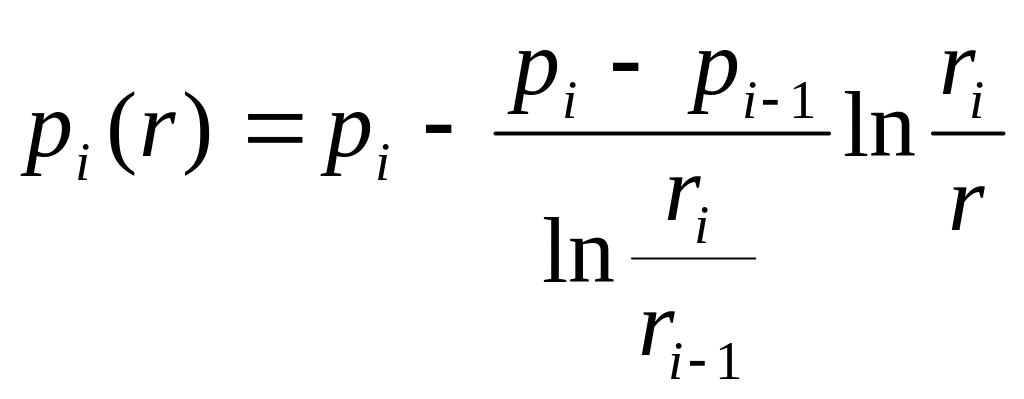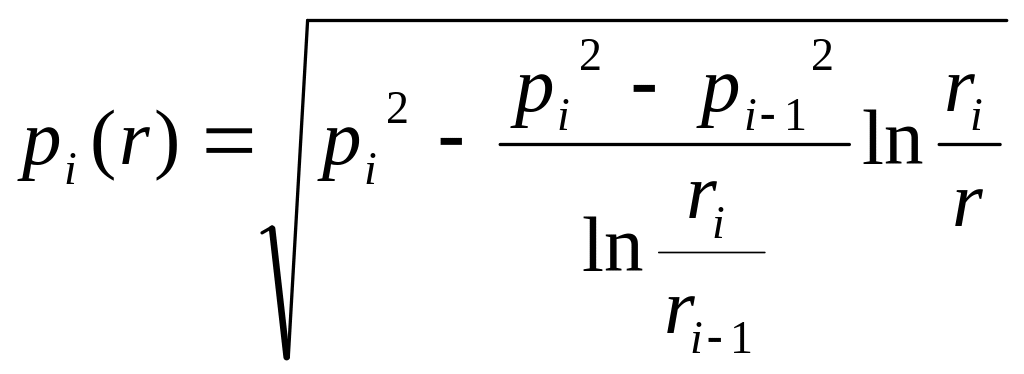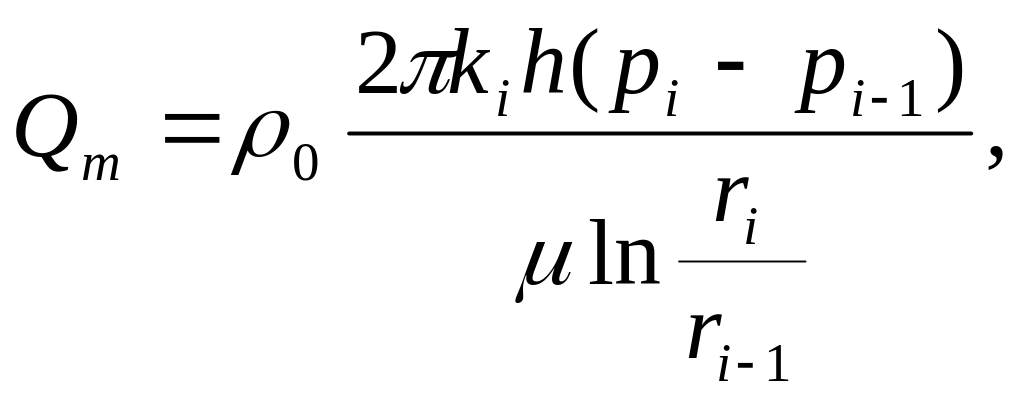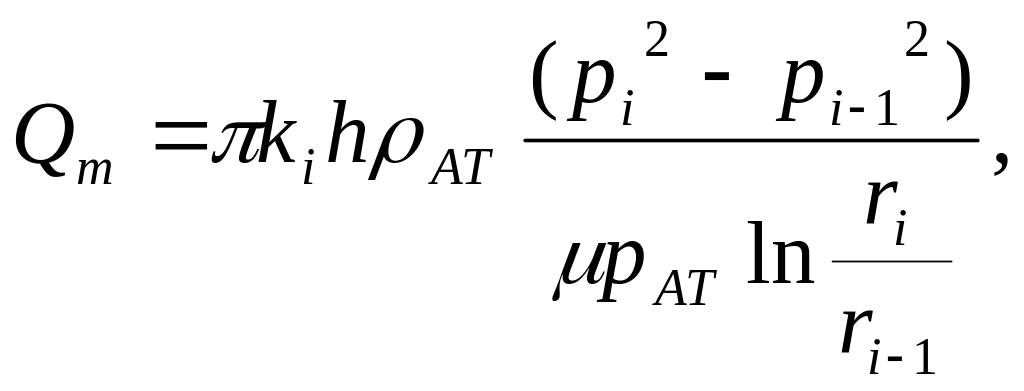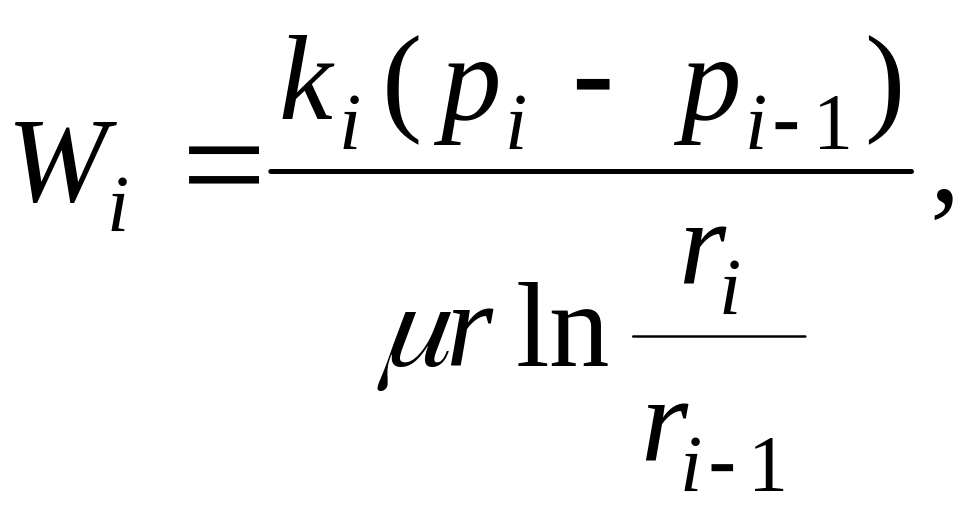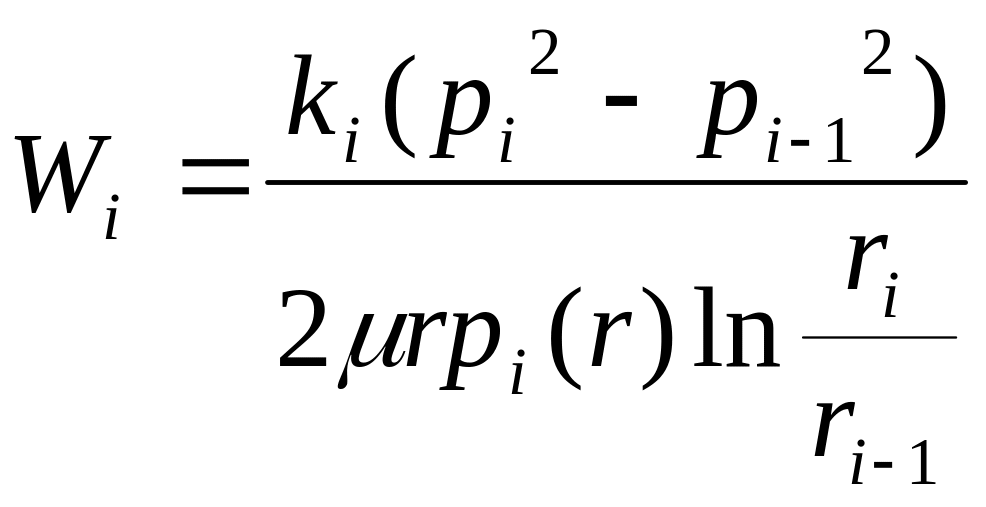3 .7.2. Плоскорадиальный поток в неоднородных пластах

А. Слоисто-неоднородный пласт.

Пусть круглый горизонтальный пласт толщина h состоит из n пропластков толщиной h_i c проницаемостью k_i и пористостью m_i, где i = 1, 2, …n. Пласт насыщен жидкостью или газом, и в нем происходит установившийся плоскорадинальный приток к центральной скважине. Контур питания удален от скважины на расстояние R_k и на нем поддерживается постоянное давление р_к, на скважине радиуса r_c поддерживается постоянное давление р_с (при этом р_к > р_с). Считаем, что перетоки между пропластками отсутствуют.

Ф ормула для распределения давления будет одинаковой для всех пропластков, а скорость фильтрации и дебит в каждом пропластке будет свои.

Б. Зонально-неоднородный пласт

Пусть имеется горизонтальный пласт толщиной h, состоящий из n кольцеобразных зон с различной проницаемостью k_i и пористостью m_i , при этом граница каждой зоны имеет форму боковой поверхности цилиндра, соосного скважине. На внешней границе n-й зоны, являющейся контуром питания пласта R_K (r_n+1 = R_K), поддерживается постоянное давление p_k= p_n, на внутренней границе пласта (r = r₁ = r_с), т.е. на забое совершенной скважины, поддерживается постоянное давление р_c. В пласте имеет место установившийся плоскорадиальный поток однородного флюида по закону Дарси.

Характерист.	Несжимаемая жидкость	Совершенный газ
Слоисто – неоднородный пласт
Распределение давления в пропластках
Массовый расход i – го пропластка
Скорость фильтрации i–го пропластка
Зонально – неоднородный пласт
Распределение давления в i – ой зоне
Массовый расход i – ой зоны
Скорость фильтрации i – ой зоны

Расчетные формулы для плоскорадиального потока несжимаемой жидкости и совершенного газа в неоднородных пластах

В пласте происходит одномерное установившееся фильтрационное течение однородного флюида. Поэтому в каждой из зон зонально-неоднородного пласта имеем фильтрационный поток с теми же расчетными формулами для давления, скорости фильтрации и дебита, что и в случае однородного пласта. Принимают в качестве давления на контуре питания и скважине - давление в начале и конце зоны, а вместо радиусов контура питания и скважины – радиусы начала и конца зоны. В каждой зоне будет одинаковый дебит, а формула распределения давления и скорости для каждой зоны будут свои. Сколько втекает в пласт через контур питания, столько и вытекает из пласта через скважину. Такой вывод следует из закона сохранения массы при установившемся течении. Следовательно, объемный дебит в каждой зоне один и тот же, но сечение пласта имеет различную площадь, поэтому скорость фильтрации в каждой зоне будет изменяться и даже внутри зоны она не будет постоянной.

Время движения частиц в каждой зоне вычисляются по формулам плоскорадиальной фильтрации для несжимаемой жидкости и совершенного газа, с той лишь разницей, что в качестве контура питания и скважины будут границы неоднородности.

Радиально-сферический приток и фильтрация в неоднородных пластах по нелинейным законам изучить самостоятельно.

Для задач, как и в случае, прямолинейно-параллельной фильтрации, формулами воспользоваться для вычисления невозможно, т.к. в постановке задачи заданы давления только на контуре питания и скважины. Поэтому вначале находят формулу для дебита, выраженную через давления, заданные в постановке задачи. Затем определяют давления на границах зон.

Контрольные вопросы и задачи. Басниев 2003, 2005

1. Какой фильтрационный поток называется одномерным? Какие бывают одномерные фильтрационные потоки?

2. Сравнить время движения меченой частицы от контура питания до забоя скважины (галереи) для случаев прямолинейно-параллельной фильтрации, плоскорадиальной и радиально-сферической фильтрации. Расстояния от контура питания до забоя скважины (галереи) равны, равны также давления на контуре питания и забое скважины (галереи), пористости и проницаемости.

3. При прямолинейно-параллельной фильтрации по закону Дарси давление в сечении 1 с координатой х₁ = 200 м составляет p₁ = 3 МПа, а в сечении 2 (х₂ = 400 м) р₂ = 1 МПа. Чему равно отношение скоростей фильтрации и градиентов давления в этих сечениях, если фильтруется:

а) несжимаемая жидкость; б) совершенный газ?

4. В двух пластах - нефтяном и газовом - длиной L = 1200 м давление на контуре питания р_К = 10 МПа, на галерее р_г = 7 МПа. Сравнить давления в обоих пластах в сечении на расстоянии х = 800 м от контура питания.

5. В круговом пласте происходит фильтрация нефти. Какую долю от общей депрессии составляет потеря давления на участке от точки с координатой r до забоя? Радиус пласта R_k = 1000 м, r_C = 0,1 м. Принять следующие значения r: 100 м, 10 м, 1 м.

Указание. Определить в процентах отношение (р - р_с)/(р_k - р_c).

6. В газовом пласте происходит установившаяся плоскорадиальная фильтрация совершенного газа к скважине по закону Дарси. Найти скорость фильтрации и среднюю скорость движения газа на расстоянии r = 10 м от центра скважины, если известны объемный приведенный дебит Q_АТ = 8•10⁵ м³/сут, толщина пласта h = 12 м, давление на контуре питания R_к = 12 МПа и на забое скважины r_с = 9 МПа; расстояние до контура питания R_k = 500 м, радиус скважины r_с = 0,1 м, пористость пласта m = 20%.

7. Сравнить средневзвешенные давления в круговых нефтяном и газовом пластах, если p_c / p_к = 0,5, R_k/r_c = 500.

8. На месторождении Карачаганак толщина продуктивного пласта так велика (≈ 1500 м), что весь интервал перфорации на скважине можно моделировать одним стоком, и приток к скважине считать радиально-сферическим. Определить эффективный радиус такого стока для скважины с дебитом Q_m = 700 т/сут, забойным давлением p_c = 35 МПа, если пластовое давление р_k = 50 МПа, проницаемость k = 10 мД; из-за высоких давлений флюид можно считать несжимаемым плотностью ρ = 500 кг/м³, вязкостью μ = 5 • 10^-5 Па·с. Гравитационными силами пренебречь.

9. Во сколько раз надо изменить радиус скважины, чтобы дебит при плоскорадиальной фильтрации нефти удвоился? Рассмотреть фильтрацию: а) по закону Дарси; б) по степенному закону при n = 4/3; в) по закону Краснопольского. Принять R_k = 800 м, r_c = 0,1 м.

10. Построить (качественно) график изменения давления р(х) вдоль полосообразного пласта, в котором движется нефть. Пласт состоит из трех зон одинаковой длины с проницаемостями к₁ > к₂ > к₃.

11. Круговой пласт состоит из двух кольцевых зон с различной проницаемостью: 1) к = к₁ при r_с < r < r₁; 2) к = к₂ при r₁ < r < R_k. Вывести формулу для определения давления р₁ на границе зон. Давления на контуре питания р_k и на забое р_c заданы.

12. Как различаются между собой градиенты давлений и скорости фильтрации на границе двух зон (r = r₁) кругового пласта с разными проницаемостями? В зоне I (r_с ≤ r ≤ r₁)к₁ = 0,9 Д; в зоне II (r₁ < r ≤ R_k)/k₂ = 0,3 Д.

13. Круговой пласт состоит из двух, слоев с соотношением проницаемостей k₁:k₂ = 1:2 и толщин h_l : h₂ = 2:3. Как различаются между собой скорости фильтрации ω₁: ω₂ в точке с одной и той же координатой r?

14. В круговом нефтяном пласте проницаемость меняется следующим образом: в призабойной зоне радиусом г₀ она увеличивается линейно от значения k₁ на забое (при r = r_с) до значения k₂ (при r = r₀); в остальной части пласта (от r₀ доR_k) проницаемость постоянна и равна k₂. Вывести формулу дебита. Толщина пласта h, вязкость жидкости μ и депрессия р_k — р_с, известны.

15. Определить дебит дренажной галереи шириной В = 50 м, если толщина пласта h = 10 м, расстояние от контура питания до галереи l = 1 км, коэффициент проницаемости пласта k = 1 Дарси, динамический коэффициент вязкости μ = 1 сП, давление на контуре питания р_к = 1960 кПА, давление на галерее р_Г = 980 кПА.

1 сП (сантипуаз) = 0,01 П (Пуаз) = 0,001 Па·с

16. Определить функцию распределения давления и найти модуль градиента давления при прямолинейно-параллельной фильтрации в пласте несжимаемой жидкости по закону Дарси. Если длина пласта 5 км, толщина пласта 10 м, ширина галереи 300 м, коэффициент проницаемости пласта 0,8 Дарси, давление на галерее 2,94 МПа, динамический коэффициент вязкости жидкости 4 сП, дебит галереи 30 м³/сутки.

17. Определить дебит нефтяной скважины (т/сут) в случае установившейся плоскорадиальной фильтрации жидкости по закону Дарси, если известно, что давление на контуре питания 9,8 МПа (100 кгс/см²), давление на забое скважины 7,30 МПа (75 кгс/см²), коэффициент проницаемости пласта 15 м, диаметр скважины 24,8 см, радиус контура питания 10 км, динамический коэффициент вязкости жидкости 6 МПа·с и плотность жидкости 850 кг/м³.

18. Определить давление на расстоянии 10 и 100 м от оси симметрии скважины при плоскорадиальной установившейся фильтрации несжимаемой жидкости по закону Дарси, если коэффициент проницаемости пласта 0,5 Дарси, толщина пласта 10 м, давление на забое скважины 7,84 МПа (80 кгс/см²), радиус скважины 12,4 см, динамический коэффициент вязкости μ = 4·10^-3 Па·с, плотность нефти 870 кг/м³, массовый дебит скважины равен 200 т/сут.

19. Определить средневзвешенное по поровому объему пласта давление, если давление на контуре питания 9,8 МПа, давление на забое скважины 7,84 МПа, расстояние от контура питания 25 км, радиус скважины 10 см.

20. Определить время отбора нефти из призабойной зоны скважины радиусом 100 м, если толщина пласта 10 м, коэффициент пористости пласта 0,20, массовый дебит нефти 40 т/сут, плотность нефти 920 кг/м³, радиус скважины 0,1 м.

21. Определить врем, за которое частица жидкости подойдет к стенке скважины с расстояния r₀=200 м, если коэффициент проницаемости пласта равен 1 Дарси, динамический коэффициент вязкости нефти равен 5 сП, депрессия во всем пласте с радиусом контура питания 1 км составляет Δр = р_к – р_с =10 кгс/см², толщина пласта 10 м, пористость пласта 0,15, радиус скважины 10 см.

22. Скважина вскрывает пласт бесконечно большой мощности на небольшую глубину. Считая движение радиально- сферическим, определить время перемещения частиц жидкости вдоль линий тока от точки с координатой 100 м до точки с координатой 5 м. Скважина эксплуатируется с постоянным дебитом 120 м³/сут, пористость пласта 15%.

23. В пласте, стоящем из трех пропластков, имеет место прямолинейно-параллельная фильтрация несжимаемой жидкости по закону Дарси. Как относятся скорости фильтрации и расходы пропластков w₁ : w₂ : w₃, Q₁ : Q₂ :Q₃, k₁ : k₂ : k₃ = 5:4:3, h₁ : h₂ : h₃ =1:2:3. Общая депрессия Δр = 3 МПа, длина пласта l = 1500 м, ширина пласта В = 100 м.

24. В центре кругового пласта радиуса R_k = 3 км расположена совершенная скважина радиуса r_c = 0,1 м. Пластовое давление p_k = 10 МПа. В начале пласт имел постоянную проницаемость

К =0,8 Д и скважина эксплуатировалась при депрессии 2 МПа, т.е. р_с =8 МПа. Затем проницаемость призабойной зоны радиуса r₁ = 20 м уменьшилась до значения К₁ = 0,1 Д. Какое забойное давление надо создать, чтобы получить тот же дебит, что и для однородного пласта?

25. В центре кругового пласта радиуса R_k = 5 км расположена совершенная скважина радиуса r_c = 0,1 м. Пластовое давление p_k = 12 МПа. В начале пласт имел постоянную проницаемость К = 0,6 Д и скважина эксплуатировалась при депрессии 3 МПа, т.е. р_с = 9 МПа. Затем проницаемость призабойной зоны радиуса r₁ = 20 м уменьшилась до значения К₁ = 0,1 Д. Какое забойное давление надо создать, чтобы получить тот же дебит, что и для однородного пласта?

26. Круговой пласт состоит из двух зон разной проницаемости /К₁ = 1 Д, К₂ = 0,2 Д/, радиус зоны неоднородности r₁ = 10м. В пласте фильтруется нефть с плотностью ρ = 760 кг/м³ и вязкостью μ = 2 мПа·с по закону Дарси. Определить скорости фильтрации и значения градиентов давления на границе зон, если r_{c =} 0,1 м, R_k = 500 м, p_k = 12 МПа, р_с = 10 МПа.

27. Проницаемость однородного пласта радиуса R_k = 1600 м равна К₀ = 1,5 Д. В результате запарафинивания пласта проницаемость прибойной зоны радиусом r₁ = 10 м снизилась до К₁ = 0,15 Д. Радиус скважины r_C = 0,1 м. Найти среднюю проницаемость пласта.

Слоисто-неоднородный пласт прямолинейно-параллельного потока и при радиальной фильтрации одинаков для несжимаемой жидкости и газа: ,

Для зонально-неоднородного пласта прямолинейно-параллельного потока для несжимаемой жидкости и газа .

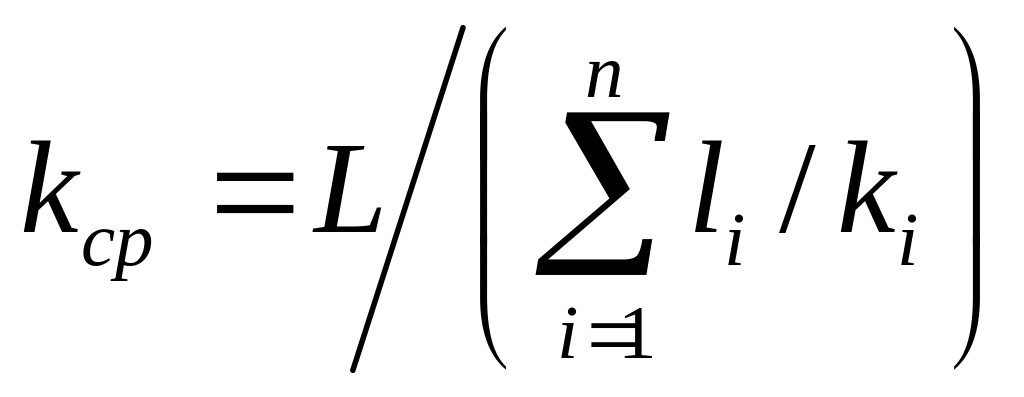Для зонально-неоднородного пласта плоскорадиального потока

28. В результате кислотной обработки призабойной зоны пласта проницаемость ее увеличилась в 2 раза на расстоянии r₁ = 5 м от скважины. Как изменится дебит скважины, если первоначальная проницаемость всего пласта К₀, радиус пласта R_k = 1000 м, а дебит Q₀.

29. Во сколько раз изменится дебит нефтяной скважины радиусом r_c = 0,1 м, эксплуатирующей пласт (R_k = 10 км, h = 10 м) проницаемость 1 Д, если проницаемость призабойной зоны радиусом r₁ = 1 м уменьшить в 5 раз.

30. В пласте состоящем из двух зон разной проницаемости, имеет место прямолинейно-параллельная фильтрация несжимаемой жидкости по закону Дарси, К₁ = 0,2 Д; К₂ = 0,6 Д; ω₁ = 10^-5 м/с, μ = 2·10^-3 Па·с. Найти градиенты давления в обеих зонах и построить график р(х).

92