3.7. Одномерные фильтрационные потоки несжимаемой жидкости и газа в неоднородных пластах по закону Дарси

В природных условиях продуктивные нефтегазосодержащие пласты редко бывают однородными. Если проницаемость, просветность, пористость, удельная повехность пласта неодинаковы в различных точках, то пласт называется неоднородным.

Нередко встречаются такие пласты, значительные области которых сильно отличаются друг от друга по фильтрационным характеристикам. Это, так называемые, макронеоднородные пласты, параметры которых существенно влияют на характеристики фильтрационных потоков. При расчетах элементарных фильтрационных потоков в макронеоднородных пластах также удобно прибегнуть к схематизации геометрии движения и найти такие эквивалентные значения коэффициентов фильтрационного сопротивления, применив которые, можно использовать полученные в предыдущем параграфе формулы для однородного пласта.

В пластах коллекторах выделяют следующие макронеоднородности:

Слоистая неоднородность, когда пласт разделяется на несколько слоев, в каждом из которых проницаемость в среднем постоянна, но отлична от проницаемости соседних слоев. Такие пласты называют также неоднородными по толщине.

Границы раздела между слоями и различными проницаемостями считают обычно плоскими. В модели слоистой пористой среды предполагается, что проницаемость меняется только по толщине пласта и является кусочной функцией вертикальной координаты.

Зональная неоднородность – пласт по площади состоит из нескольких зон различной проницаемости. В пределах одной и той же зоны проницаемость в среднем одинакова, но на границе двух зон скачкообразно изменяется. Таким образом, имеет место неоднородность по площади пласта.

Неоднородные пласты – проницаемость является известной непрерывной или случайной функцией координат точек области фильтрации.

Таким образом, в результате схематизации фильтрационных потоков можно выделить:

1) прямолинейно-параллельный, плоскорадиальный и радиально-сферический потоки в слоисто-неоднородном пласте;

2) прямолинейно-параллельный, плоскорадиальный и радиально-сферический потоки в зонально-неоднородном пласте;

3) прямолинейно-параллельный, плоскорадиальный и радиально-сферический потоки в пластах, где проницаемость является непрерывной или случайной функцией координат точек области фильтрации.

3.7.1. Прямолинейно – параллельный поток в неоднородных пластах

А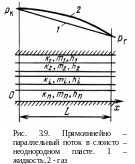 . Слоисто-неоднородный пласт.

Пусть горизонтальный пласт постоянной толщины h и ширины В состоит из n пропластков толщиной h_i, с проницаемостью k_i и пористостью m_i где i номер пропластка = 1, 2, n (рис. 3.9).

Пласт насыщен жидкостью или газом. Если на контуре питания пласта поддерживать постоянное давление р_К, а на другой его границе галерее, отстоящей от контура питания на расстоянии L, поддерживать также постоянное давление р_Г (при этом р_Г < р_К), то в каждом пропластке при отсутствии перетоков между ними будет иметь место установившийся прямолинейно-параллельный поток.

Формула для распределения давления будет одинаковой для всех пропластков, а скорость фильтрации и дебит будут в каждом пропластке свои. Это различие объясняется тем, что депрессия на пласт во всех пропластках одинакова, в фильтрационные свойства и размеры пропластков различны. Где выше проницаемость будет выше скорость фильтрации, а дебит будет больше там, где больше размеры сечения пропластка и выше проницаемость.

Б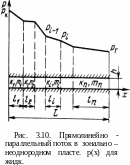 . Зонально-неоднородный пласт.

Пусть горизонтальный пласт постоянной толщины h и ширины В состоит из n зон различной проницаемости к_i, пористости m_i и длины l_i. На границах пласта поддерживаются постоянные давления р_K и р_г (р_K > р_Г) (рис. 3.10). Границы каждой зоны пласта перпендикулярны направлению фильтрационного потока вдоль оси х. В пласте происходит установившееся прямолинейно-параллельное движение однородного флюида. Поэтому в каждой из зон зонально-

Харак-ка	Несжимаемая жидкость		Совершенный газ
Слоисто – неоднородный пласт прямолинейно-параллельной фильтрации
Распределение давления в пропластках
Массовый расход i – го пропластка
Массовый расход всего пласта
Скорость фильтрации в пропластке
Время движения частиц в i – ом пропластке		,
Зонально – неоднородный пласт прямолинейно-параллельной фильтрации
Распределение давления в i – ой зоне
Массовый расход i – ой зоны
Массовый расход пласта
Скорость фильтрации i – ой зоны
Время движения частиц вдоль i – ой зоны			,

неоднородного пласта имеем прямолинейно-параллельный фильтрационный поток. По сравнению со слоисто-неоднородным пластом, в котором формула для распределения давления была одинаковой для всех пропластков, но в каждом пропластке были разные скорости фильтрации и дебит, в данном случае в каждой зоне будут одинаковые скорость фильтрации и дебит, а формула для распределения давления в каждой зоне будет своя. Сколько втекает в пласт через контур питания, столько и вытекает из пласта через галерею. Такой вывод следует из закона сохранения массы при установившемся течении для трубки тока. Следовательно, объемный дебит в каждой зоне один и тот же, но сечение пласта имеет постоянную площадь, поэтому скорость фильтрации в каждой зоне тоже постоянна.
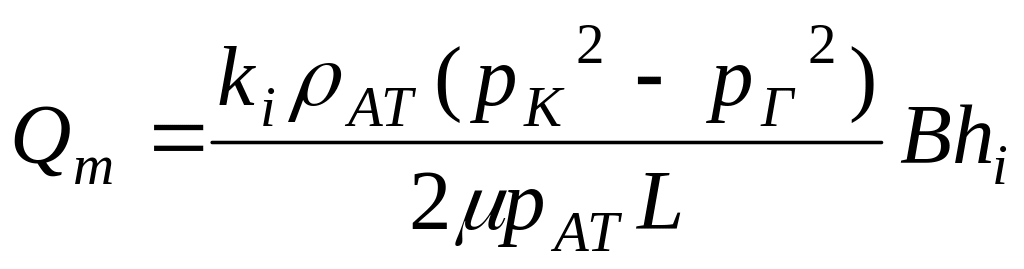
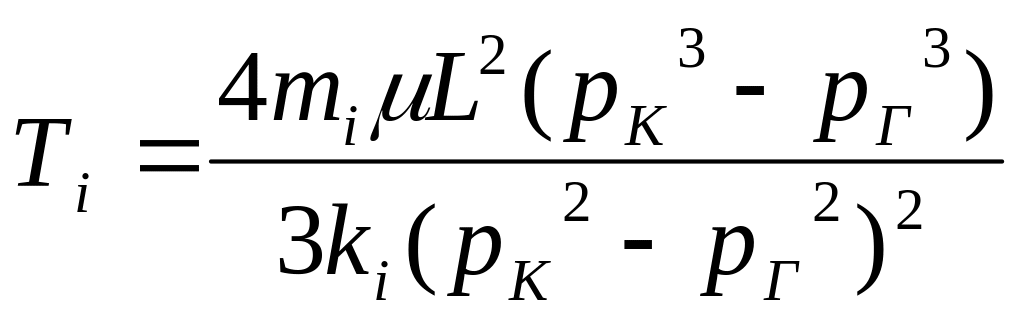
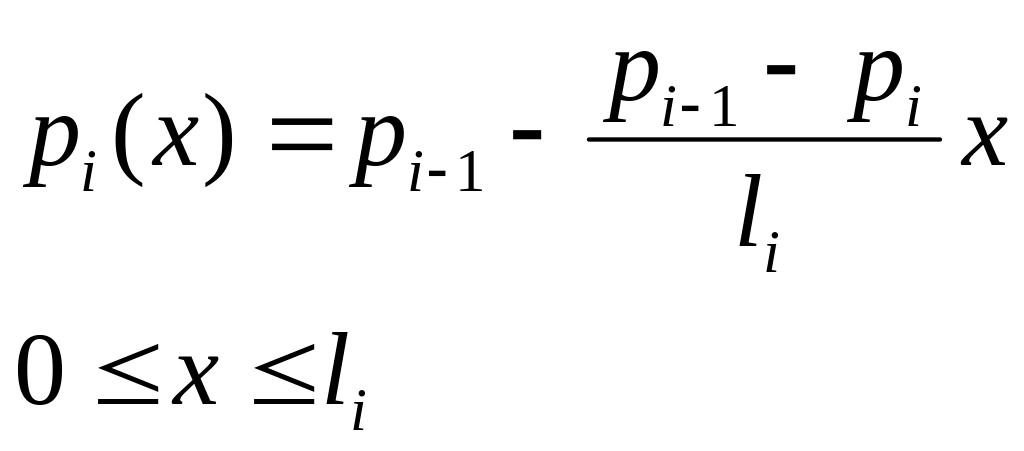
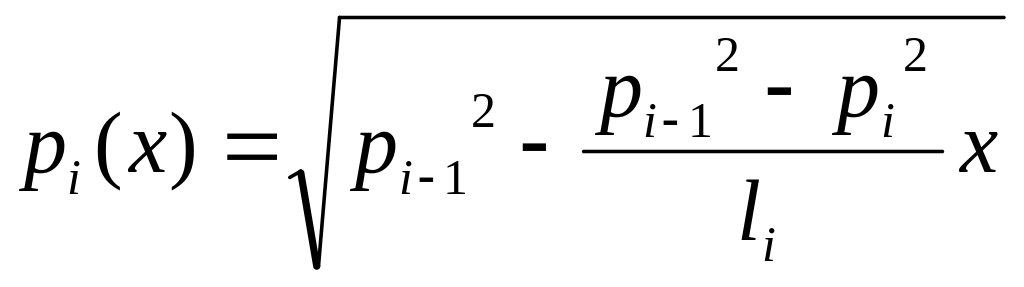
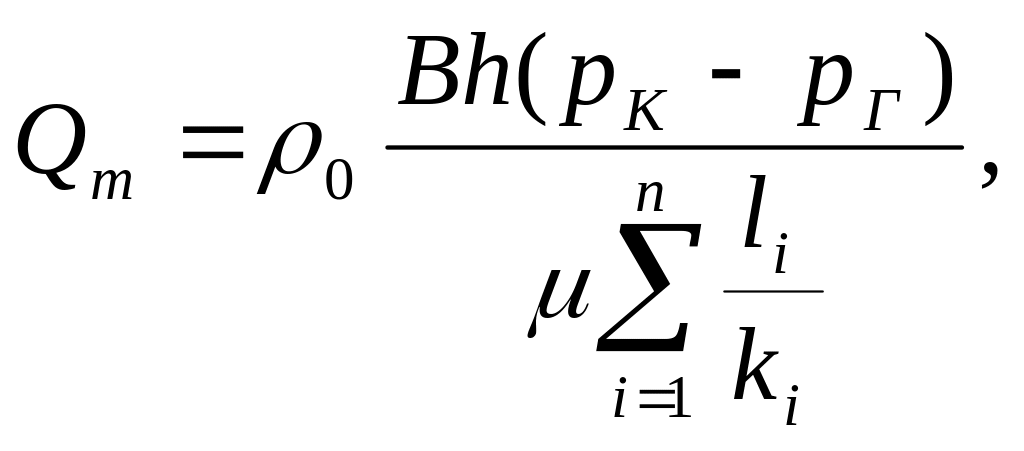
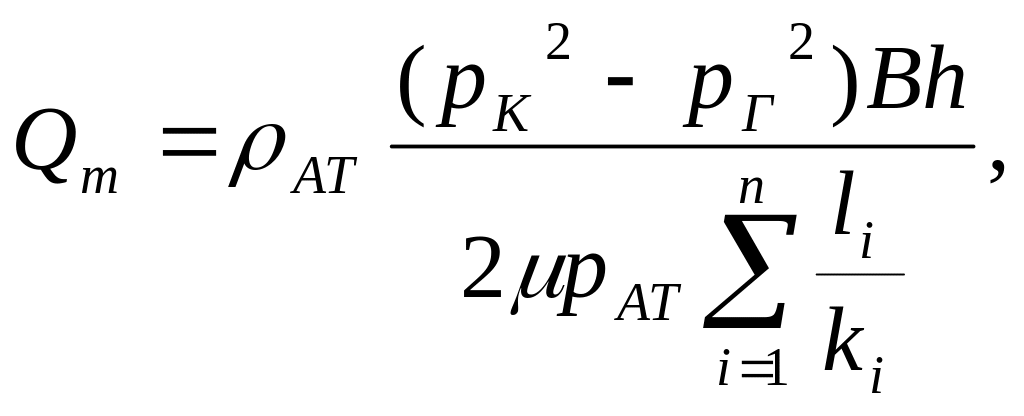
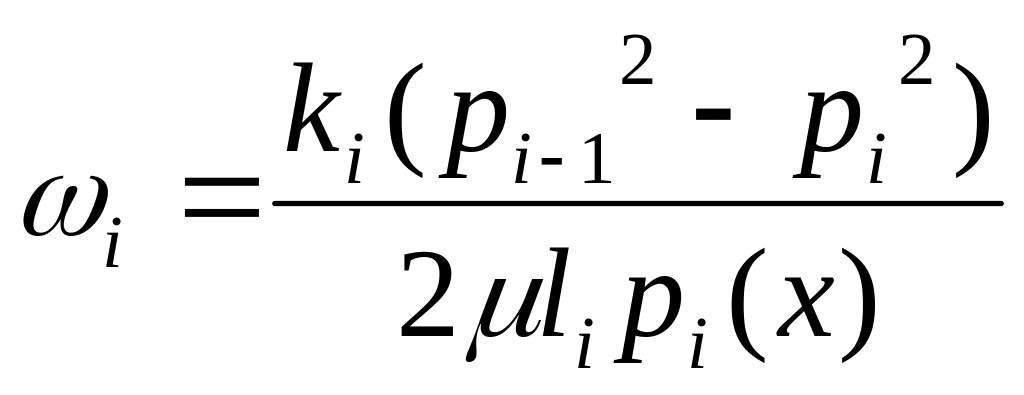