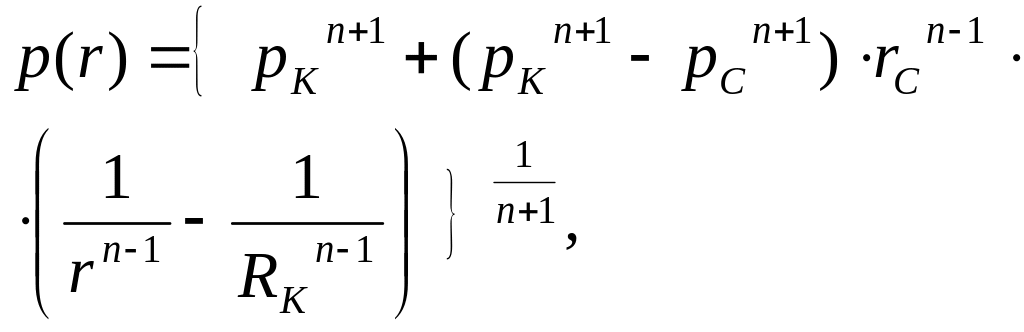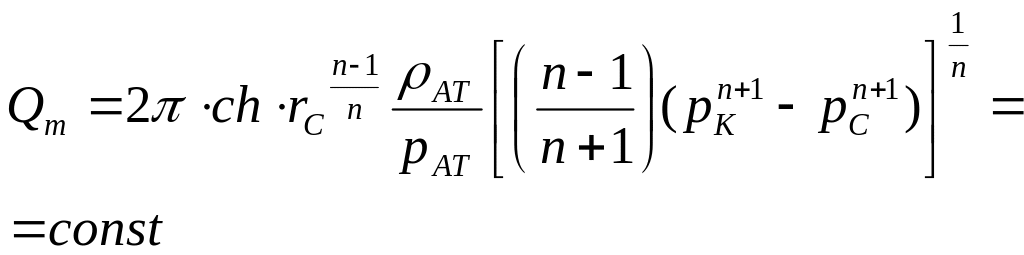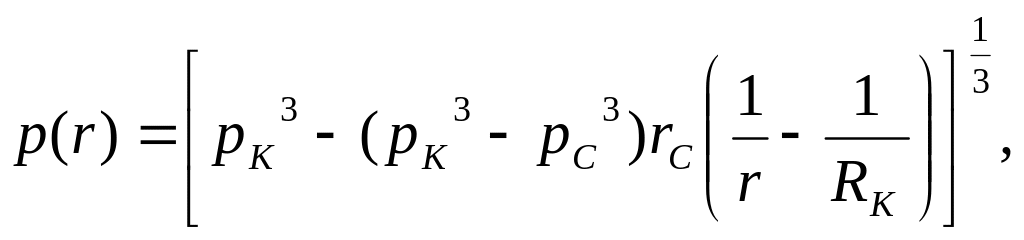3.6. Плоскорадиальный фильтрационный поток несжимаемой жидкости и газа по степенному закону фильтрации

Степенной закон фильтрации

, (3.30)

где - модуль вектора градиента фильтрационного давления,

а, n – материальные константы пористой среды. n = 1 – 2. Если n = 2, то формула (3.30) называется формулой Краснопольского, который положил, что при отклонении от закона Дарси зависимость между градиентом давления и скоростью фильтрации квадратичная.

Степенной закон фильтрации можно использовать при любых скоростях фильтрации и при нарушении закона Дарси, т.е. при Re ≥ Re_кр.

Спроектируем степенной закон фильтрации на цилиндрическую систему координат и для плоскорадиального фильтрационного потока получим:

При плоскорадиальном движении закон приобретает вид:

, , (3.31)

где с и n – константы, определяемые из опыта или по результатам исследования скважины.

Для вывода формул введем функцию давления для несжимаемой жидкости и совершенного газа соответственно получаем:

, (3.32)

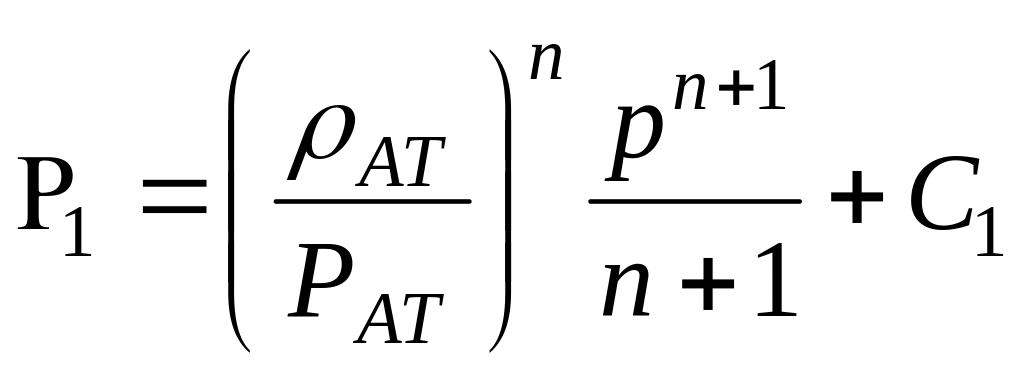. (3.33)

Расчетные формулы для плоскорадиального течения несжимаемой жидкости и газа по степенному закону

Хар-ка	Несжимаемая жидкость	Совершенный газ
Распределение давления р(r) rc ≤ r ≤ Rk
Массовый расход
Скорость фильтрации
Распределение давления р(r)	n=2 модель Краснопольского
Массовый расход Qm

Как следует из формулы распределения давления (1 строка табл.) кривая распределения давления для несжимаемой жидкости имеет форму гиперболы степени n-1, т.е. воронка депрессии будет гиперболоидом вращения. Крутизна воронки депрессии у стенок скважины больше, чем у логарифмической кривой плоскорадиального потока (стр.74). Кривая р(r) для газа (формула 1 строка 2 колонка) располагается еще выше, чем для жидкости (при тех же значениях р_к и р_с). Расчеты показывают, что для любых значений р_с, р_к, r_c, R_к на расстоянии от r = 1 м до стенки скважины теряется более 80% от общей депрессии (р_к – р_с).

М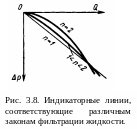 ассовый расход для жидкости (формула 2 строка 1 колонка) пропорционален депрессии в степени 1/n, поэтому индикаторная линия Q =f(Δp) при 1 < n < 2 будет иметь вид выпуклой к оси дебитов степенной кривой с дробным показателем меньшем 2. В случае фильтрации по закону Краснопольского, как показывает формула (5 строка 1 колонка), индикаторная линия является параболой второго порядка. На рис. 3.8 приведены индикаторные линии для течения несжимаемой жидкости при линейном законе фильтрации (n = 1) и при нелинейных законах: 1 < n < 2 и n = 2. Все сказанное относится также к индикаторным линиям для газа, если строить их в координатах Q_m (или Q_АТ) и . Для жидкости, и для газа величина расхода пропорциональна радиусу скважины в степени (n -1)/n (для закона Краснопольского ), т. е. эта зависимость гораздо более сильная, чем в случае выполнения закона Дарси.

Скорость фильтрации вдоль линии тока изменяется при нелинейном законе так же, как при линейном, для жидкости ω обратно пропорциональна r, для газа - обратно пропорциональна rр(r).