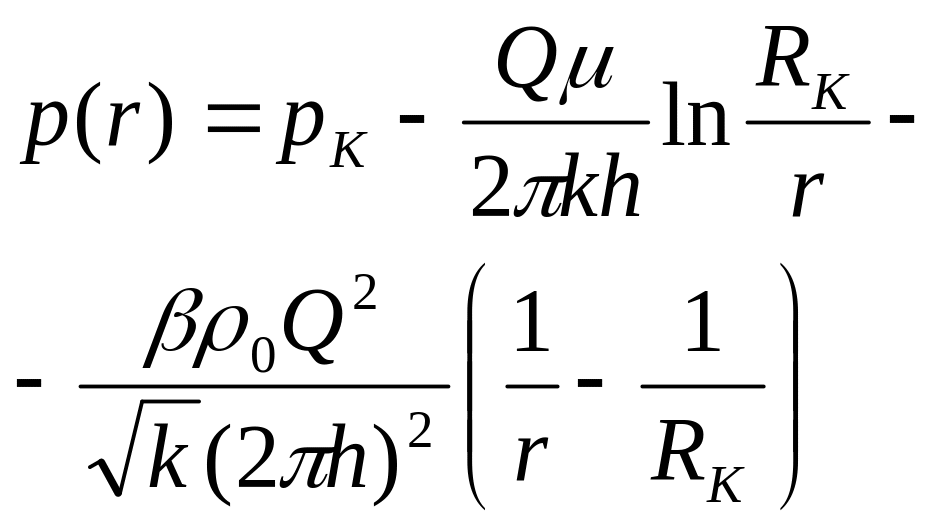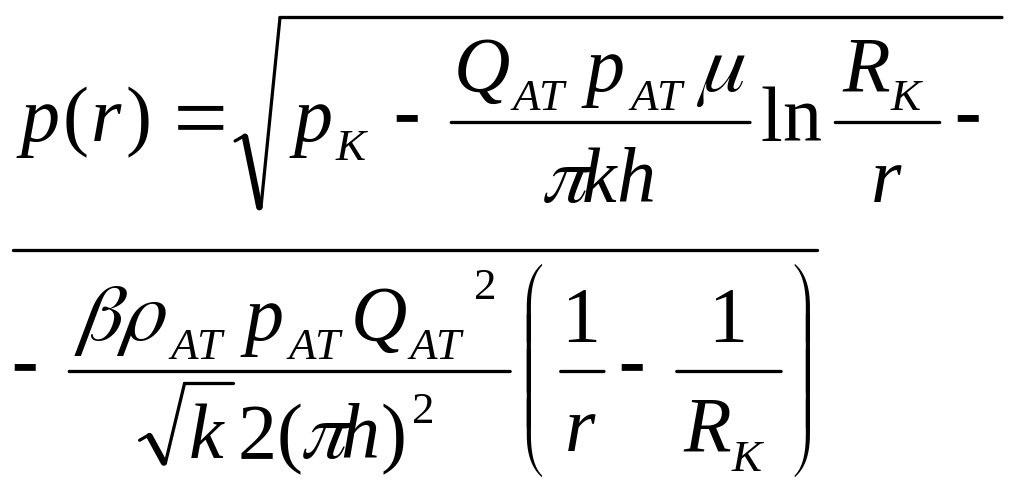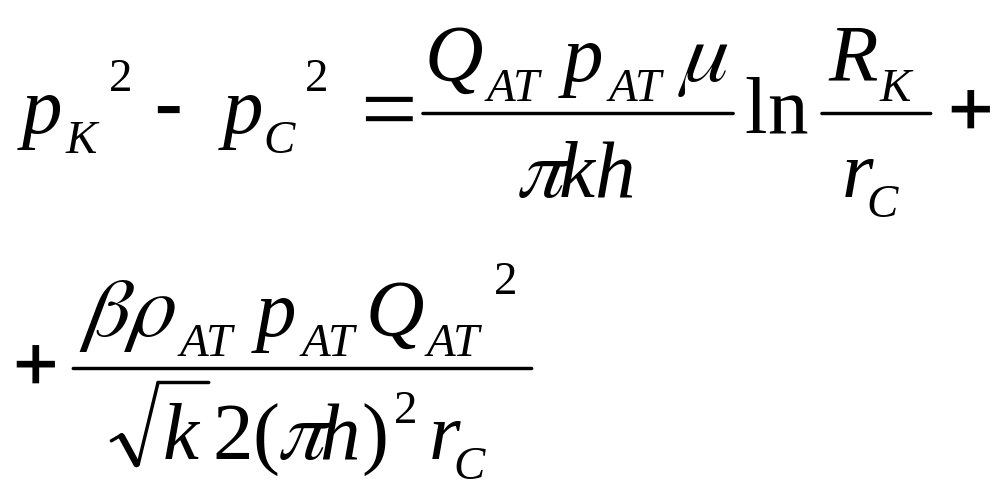3.4. Фильтрационное плоскорадиальное течение реального газа по закону Дарси

Предположим, что проницаемость постоянная, а плотность связана с давлением, то уравнение состояния для реального газа

,

где z – коэффициент сверхсжимаемости газа, учитывает отклонения реального газа от совершенного газа.

Функция Лейбензона .

Функцию Лейбензона можно использовать для решения одномерных задач фильтрации сжимаемых флюидов с учетом зависимости от давления, вязкости и коэффициента сверхсжимаемости. Тогда формула для массового дебита будет

,

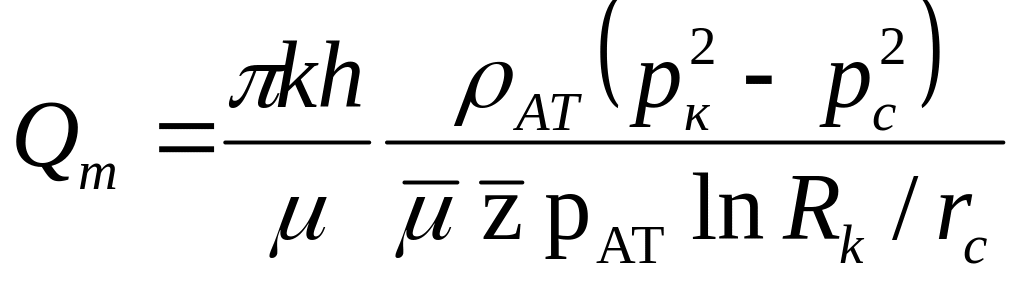где - средние арифметические значения.

Учет коэффициента сверхсжимаемости и зависимости вязкости от давления приводит к увеличению дебита на 30%.

3.5. Плоскорадиальный фильтрационный поток несжимаемой жидкости и газа по двучленному закону фильтрации

Рассмотрим способы определения основных характеристик потока при плоскорадиальном движении жидкости и газа с большими скоростями, когда причиной отклонения от закона Дарси становятся значительные инерционные составляющие общего фильтрационного сопротивления.

Двучленный закон фильтрации спроектируем на линию тока (на координатную ось r цилиндрической системы координат) и в результате получим

(3.20)

где Р – функция Лейбензона.

После проведения интегрирования, получим

Модель флюида

Характерист	Несжимаемая жидкость	Совершенный газ
Функция Лейбензона
Распределение давления в пласте rC ≤ r ≤ Rk
Уравнение притока к скважине

Индикаторная линия, построенная в координатах для жидкости и для газа , является параболой (рис. 3.5, 3.6).

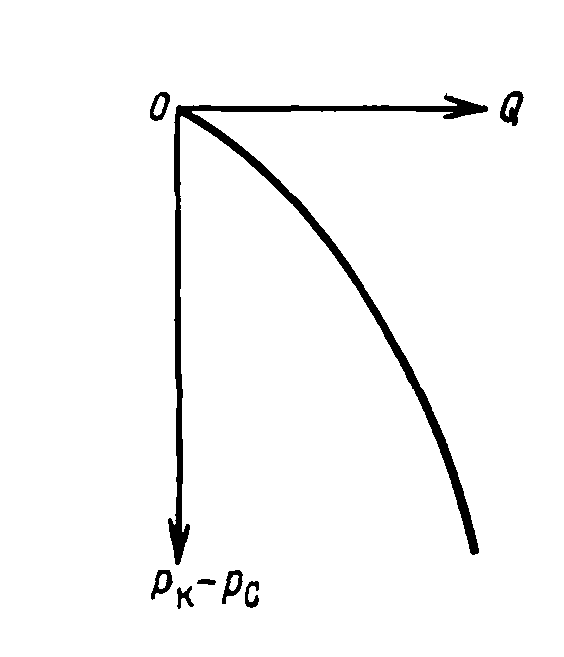
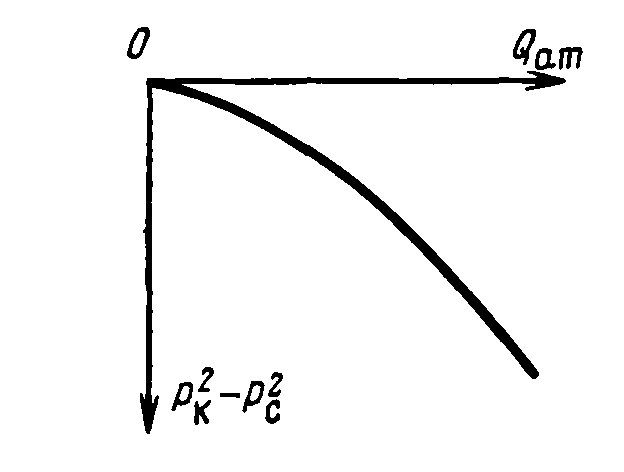
Рис. 3.5. Индикаторная линия при фильтрации жидкости по двучленному закону.	Рис. 6. Индикаторная линия при фильтрации газа по двучленному закону.

Уравнение притока к скважине можно записать в другом виде

для несжимаемой жидкости:

(3.21)

для газа

(3.22)

где

(3.23)

(3.24)

А, В, А1, В1, - коэффициенты фильтрационного сопротивления, являются постоянными для данной скважины. Определяются опытным путем при установившихся режимах.

Скважины исследуют на пяти-шести режимах, на каждом режиме измеряется дебит и определяется забойное давление. Затем скважину закрывают остановленной и давление на забое остановленной скважины принимают за контурное давление р_к.

Уравнения (3.21) и (3.22) приводят к уравнению прямой линии:

(3.25)

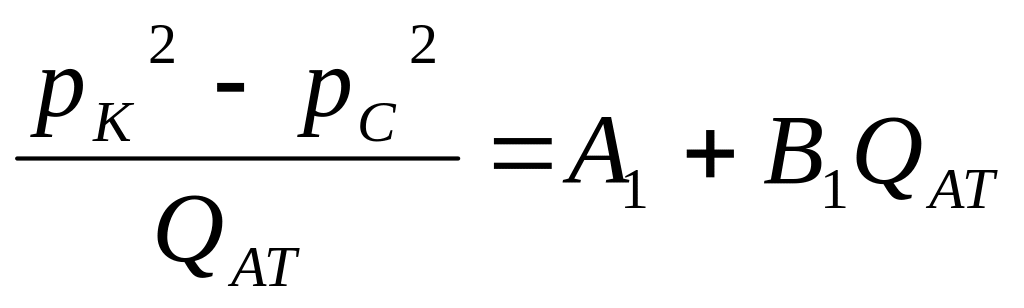(3.26)

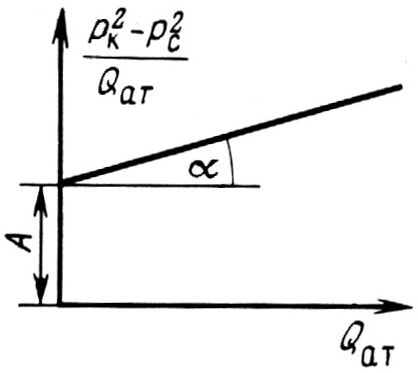
Рис. 3.7. График зависимости 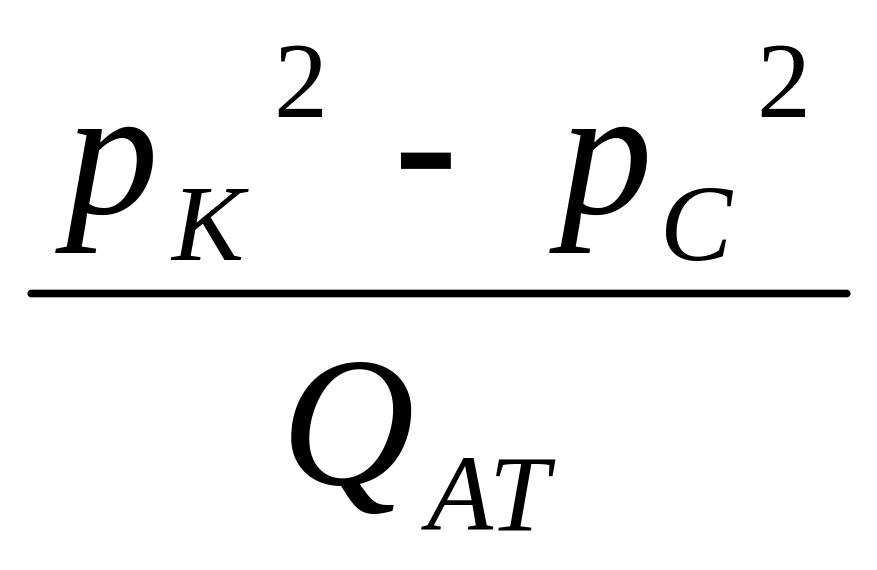от при фильтрации газа по двучленному закону.

Коэффициент А(А₁) – отрезок, отсекаемый на оси ординат, В (В₁) – тангенс угла наклона прямой к оси абсцисс.

По значениям коэффициентов А и В определяют коллекторские свойства пласта, например, коэффициент гидропроводности:

для нефтяной скважины (3.27)

для газовой скважины . (3.28)

Уравнение притока реального газа к скважине по двучленному закону фильтрации имеет вид

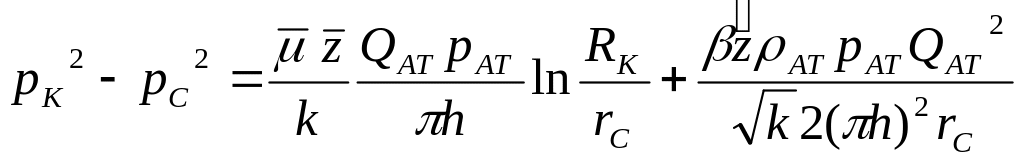(3.29)

В реальных условиях нельзя считать, что во всем пласте от стенки скважины до контура питания - справедлив единый нелинейный закон фильтрации. При значительных дебитах закон Дарси нарушается в некоторой области вблизи забоя скважины, в то время как в остальной части пласта по-прежнему соблюдается линейный закон. При увеличении дебита область, в которой нарушен закон Дарси, расширяется. В этих случаях используется двучленный закон фильтрации.