
- •Тема 2. Математические модели однофазной фильтрации
- •2.1. Закон сохранения массы.
- •2.2. Закон сохранения количества движения (импульса) (вывод по н.Е. Жуковскому)
- •2.3. Замыкающие уравнения. Математические модели изотермической фильтрации
- •2.3.1. Модели однофазной фильтрации по закону Дарси в недеформируемом пласте
- •2.3.2. Вывод дифференциального уравнения неустановившейся фильтрации однородного флюида по закону Дарси. Функция л. С. Лейбензона.
- •2.3.2 Зависимость параметров флюидов и пористой среды от давления
- •2.3.3. Начальные и граничные условия
- •Тема 3. Одномерная установившаяся фильтрация несжимаемой жидкости и газа в пористой среде
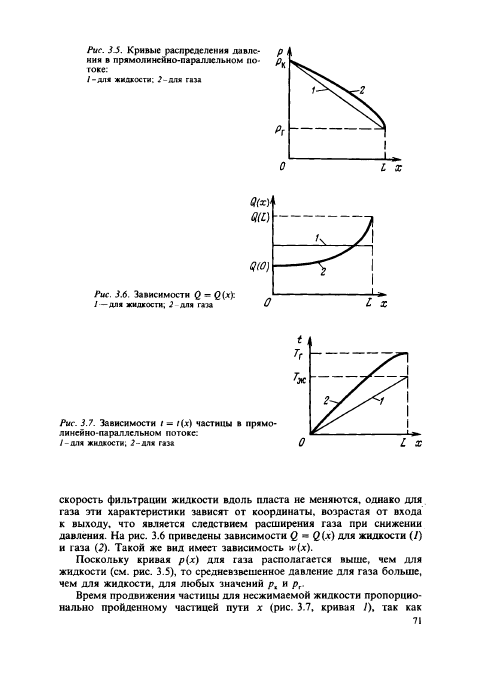
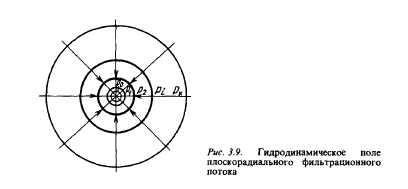
- •3.1. Схемы одномерных фильтрационных потоков
- •3.2. Характеристики одномерных фильтрационных потоков жидкости и газов
- •Прямолинейно – параллельная фильтрация несжимаемой жидкости
- •П лоскорадиальная фильтрация несжимаемой жидкости
- •Радиально – сферическая фильтрация несжимаемой жидкости
- •3.3. Анализ одномерных потоков несжимаемой жидкости и газа
- •Прямолинейно – параллельный поток несжимаемой жидкости и совершенного газа
- •Плоскорадиальный фильтрационный поток
- •Радиально – сферический фильтрационный поток несжимаемой жидкости и совершенного газа
- •3.4. Фильтрационное плоскорадиальное течение реального газа по закону Дарси
- •3.5. Плоскорадиальный фильтрационный поток несжимаемой жидкости и газа по двучленному закону фильтрации
- •3.6. Плоскорадиальный фильтрационный поток несжимаемой жидкости и газа по степенному закону фильтрации
- •3.7. Одномерные фильтрационные потоки несжимаемой жидкости и газа в неоднородных пластах по закону Дарси
- •3.7.1. Прямолинейно – параллельный поток в неоднородных пластах
- •3 .7.2. Плоскорадиальный поток в неоднородных пластах
Плоскорадиальный фильтрационный поток
При фильтрации газа массовый и объемный
приведенный дебиты (формулы в таблице)
прямо пропорциональны разности квадратов
давления
![]() ,
индикаторная линия строится в координатах
Qaт
и
и имеет прямолинейный характер (рис.).
,
индикаторная линия строится в координатах
Qaт
и
и имеет прямолинейный характер (рис.).
Важной характерной особенностью формул, определяющих дебит жидкости и газа, является слабая зависимость дебита от радиуса контура питания RK, и от радиуса скважины rс, так как эти радиусы входят в формулы под знаком логарифма.
Характеристика |
Несжимаемая жидкость |
Совершенный газ |
Функция Лейбензона |
|
|
Распределение давления по пласту
|
|
|
Массовый расход Qm
|
|
|
Массовая скорость фильтрации ω
|
|
|
Объемный расход Q
|
(формула Дюпюи) |
|
Объемная скорость фильтрации
|
|
|
Средневзвешенное давление |
|
|
Время движения отмеченных частиц
|
|
|
Время движения частицы от контура до забоя Т |
|
|
Массовая и объемная скорости фильтрации для жидкости (формулы в таблице) возрастают по мере приближения к скважине по гиперболическому закону, такой же закон справедлив для массовой скорости фильтрации газа. Объемная же скорость фильтрации газа возрастает вблизи скважины еще более резко, так как в знаменателе формулы появляется давление р(r), которое тоже уменьшается вблизи скважины.
Средневзвешенное давление имеет особое
значение для расчетов, связанных с
фильтрацией газа, так как оно определяет
запасы газа в пласте. Если по формуле
провести расчеты для различных значений
рк, рс, Rk,
rс, то можно убедиться,
что средневзвешенное пластовое давление
газа в круговом пласте ¯p
близко к контурному
![]() .
Физически это объясняется значительной
крутизной воронки депрессии при притоке
газа к скважине. Средневзвешенное
давление используется для приближенного
расчета гидродинамических характеристик;
замена его контурным значительно
упрощает расчеты.
.
Физически это объясняется значительной
крутизной воронки депрессии при притоке
газа к скважине. Средневзвешенное
давление используется для приближенного
расчета гидродинамических характеристик;
замена его контурным значительно
упрощает расчеты.
Радиально – сферический фильтрационный поток несжимаемой жидкости и совершенного газа
Как следует из формулы распределения давления несжимаемой жидкости, давление в любой точке пласта, в котором происходит радиально-сферическая фильтрация жидкости, р(r) обратно пропорционально координате этой точки. Значит, р(r) - гиперболическая кривая, причем очень крутая вблизи значения r = rс. Семейством изобар являются концентрические полусферы r = const.
Характеристика |
Несжимаемая жидкость |
Совершенный газ |
Функция Лейбензона |
|
|
Распределение давления р(r), rc ≤ r ≤RK
|
|
|
Массовый расход Qm |
|
|
Массовая скорость фильтрации |
|
|
Объемный расход
|
|
|
Объемная скорость фильтрации
|
|
|
Время движения частиц t |
|
____________ |
Время движения от контура до забоя |
|
|
Надо учесть, что под давлением в этой формуле понимается приведенное давление, отсчитываемое, например, от кровли пласта; чтобы найти истинное давление в каждой точке, надо к приведенному давлению прибавить выражение ρоgz, где z - глубина точки пласта, отсчитываемая от кровли.
Для газа кривая р(r) (формула распределения давления газа) будет более крутой вблизи забоя, чем для жидкости.
Скорость фильтрации для жидкости обратно пропорциональна r2. Если построить для радиально-сферического потока жидкости график зависимости ω(r), то крутизна кривой у стенки скважины при малых значениях r будет еще больше, чем в плоскорадиальном потоке. То же относится к газу, так как в формуле в знаменателе добавляется значение р(r).
Средневзвешенное давление практически
совпадает с контурным![]() .
.

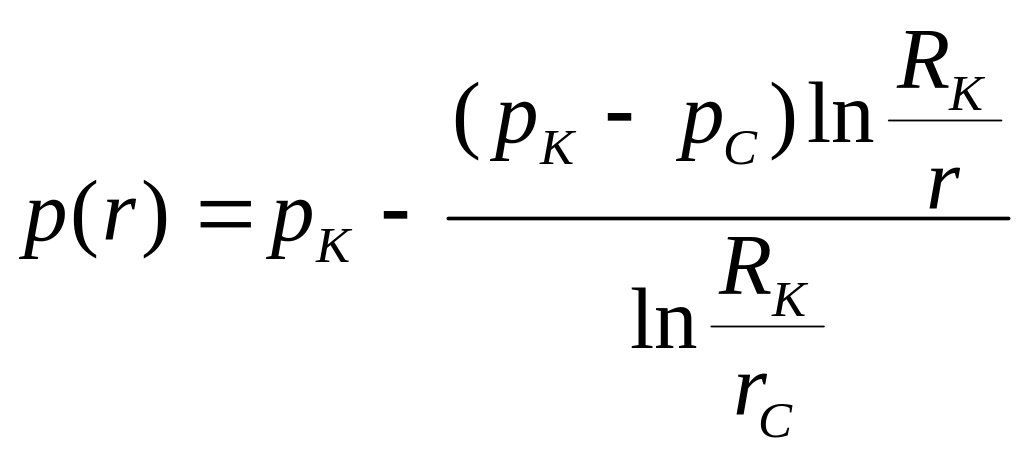
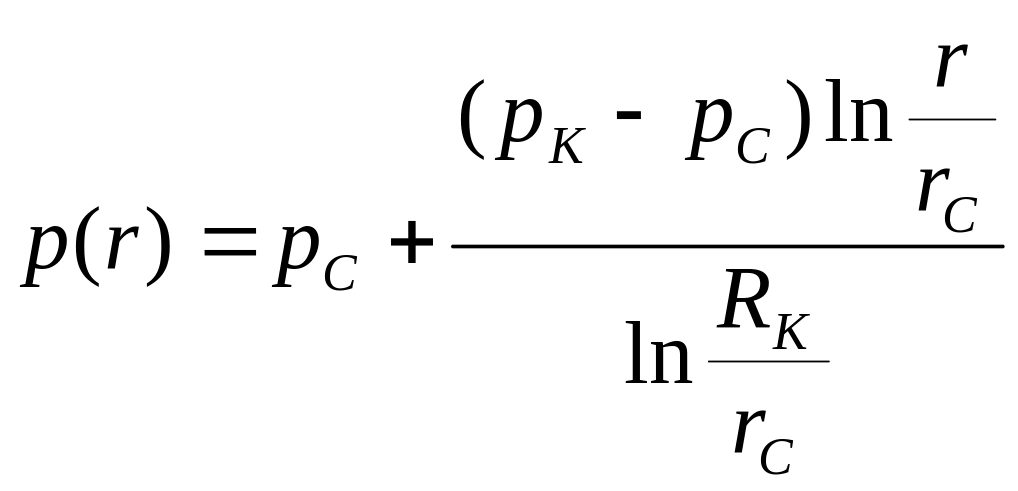
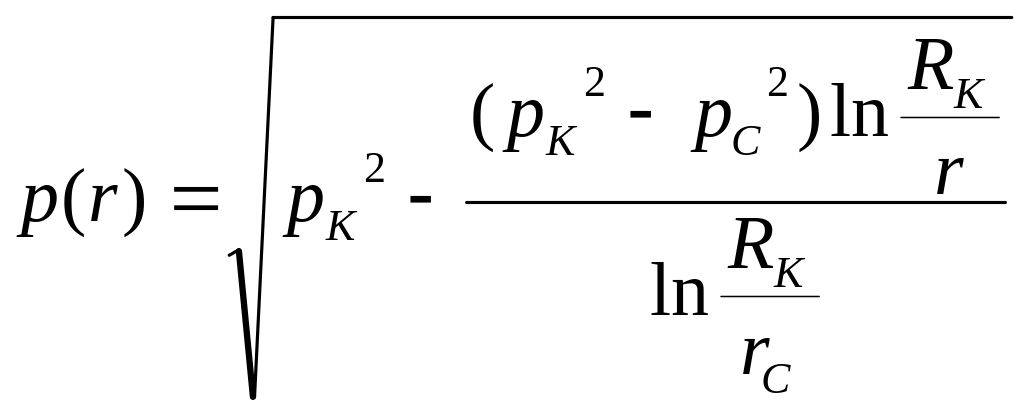
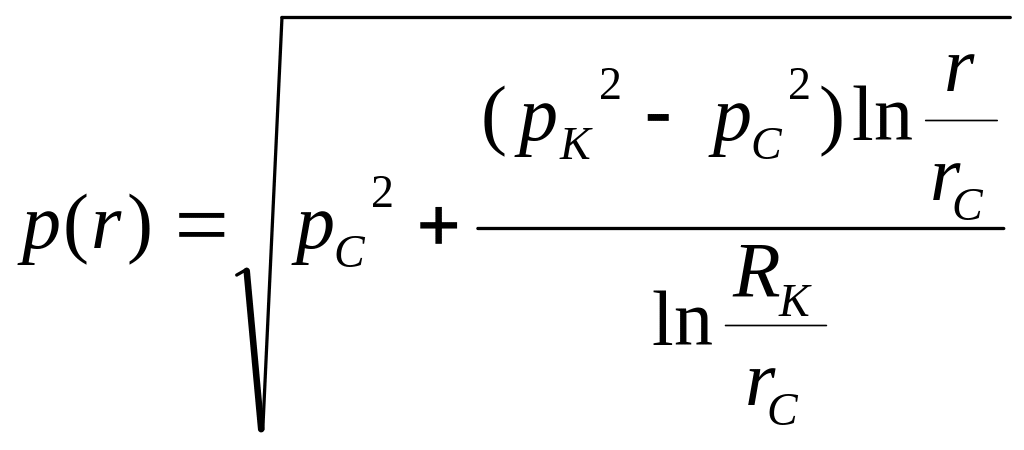
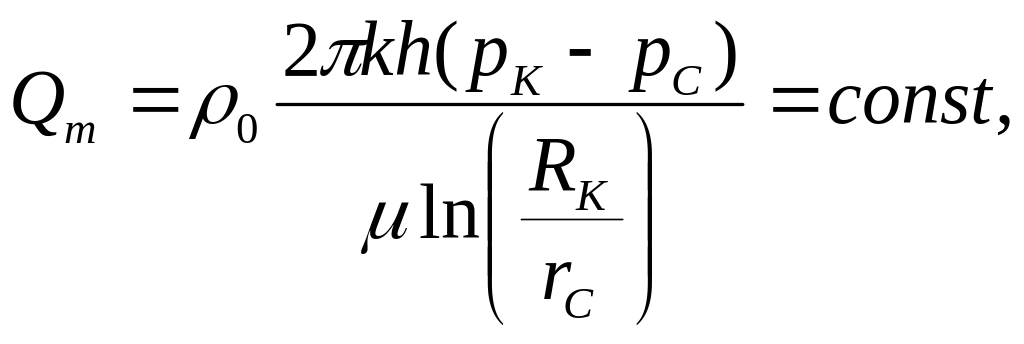
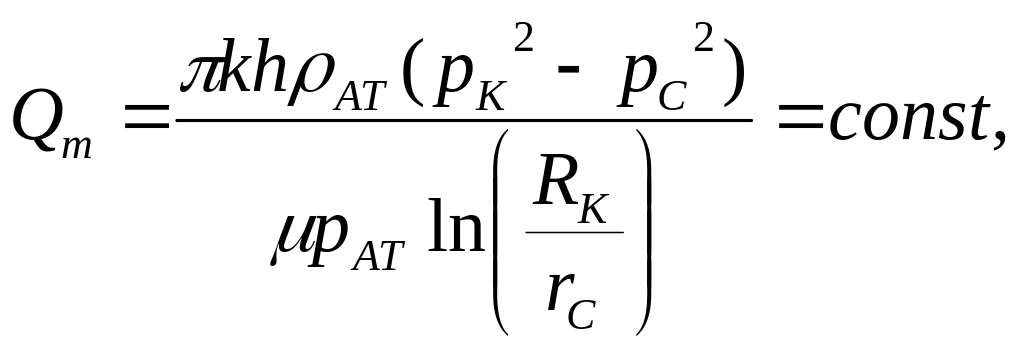
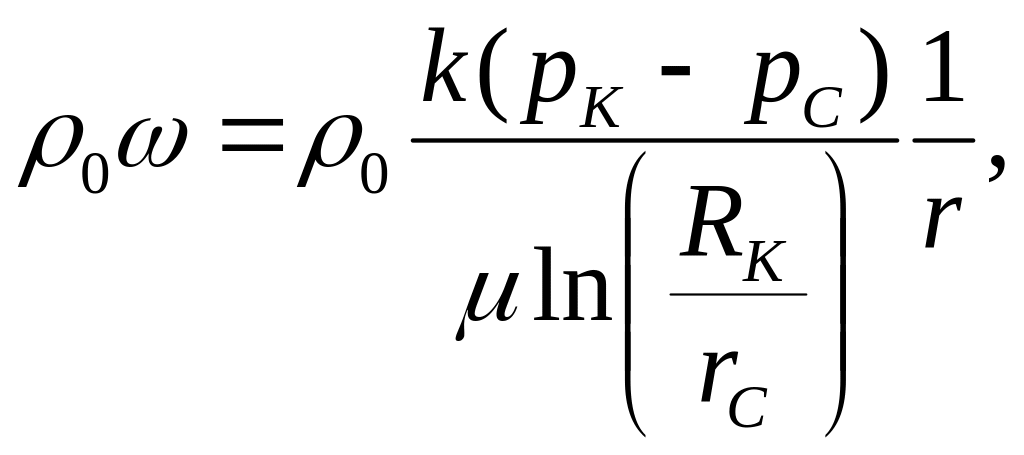
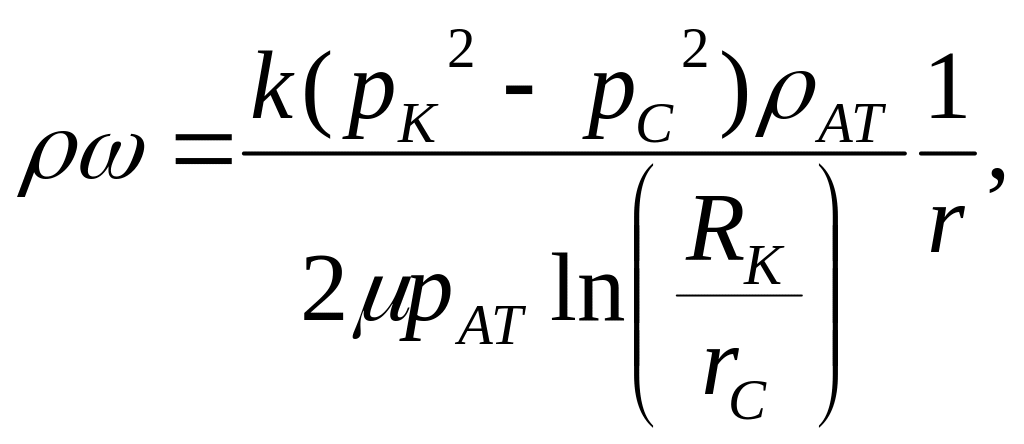
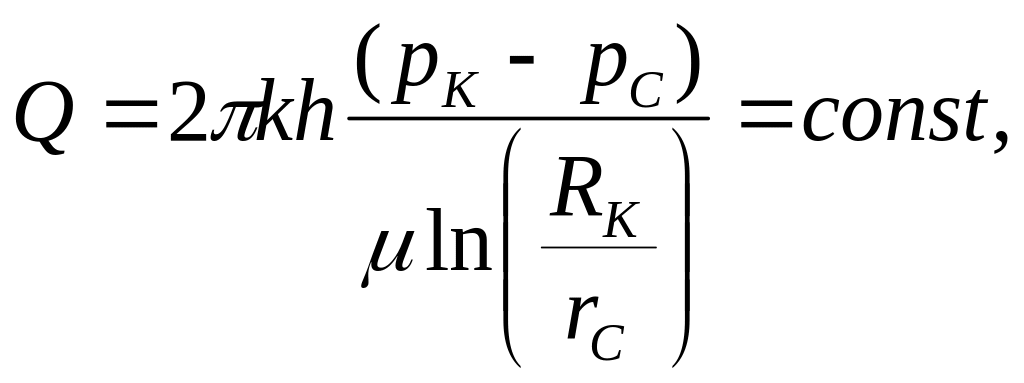
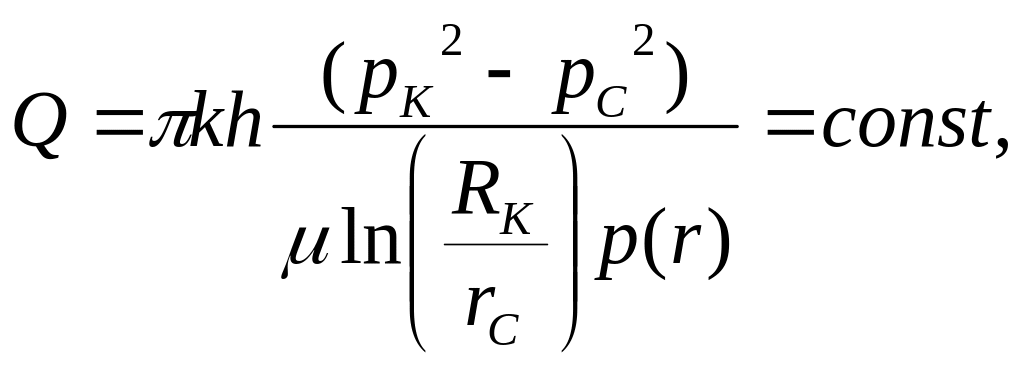
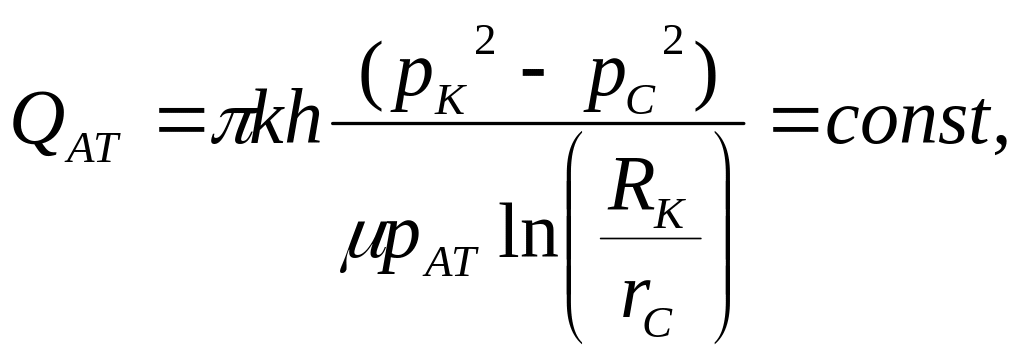
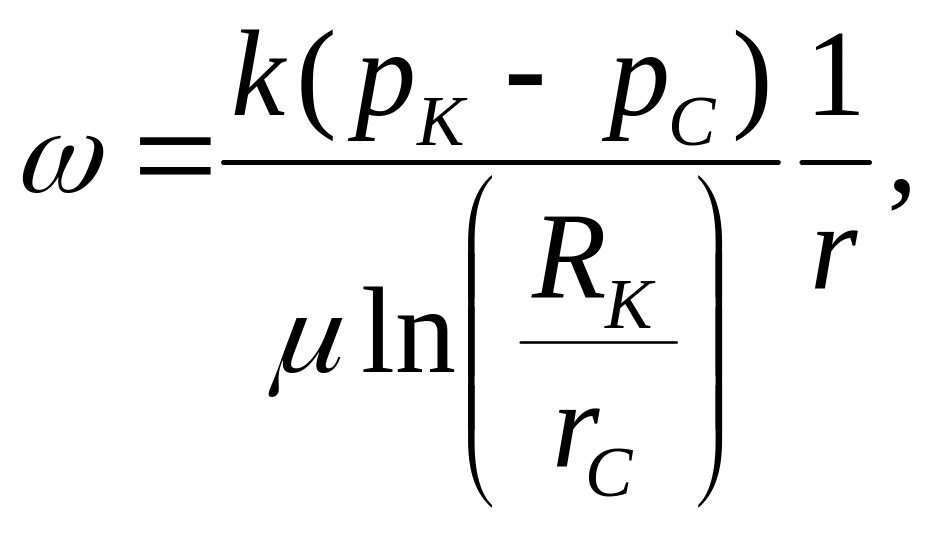
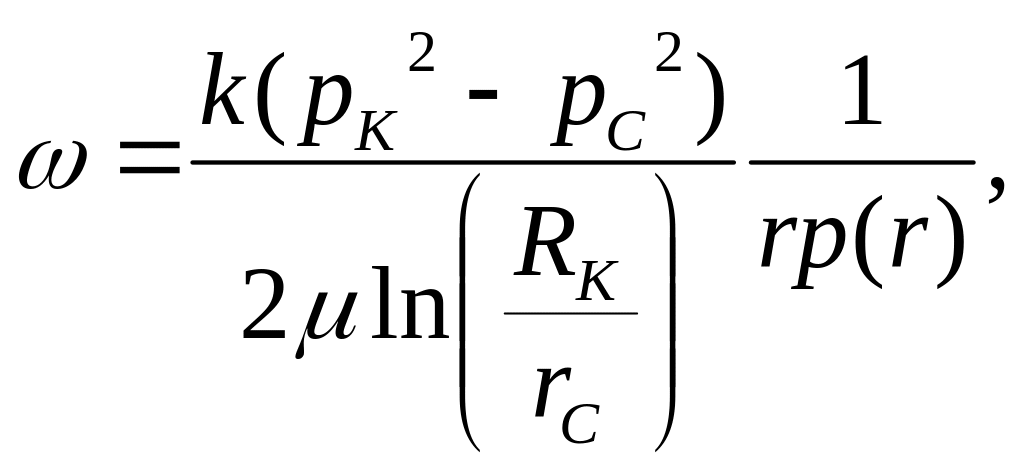
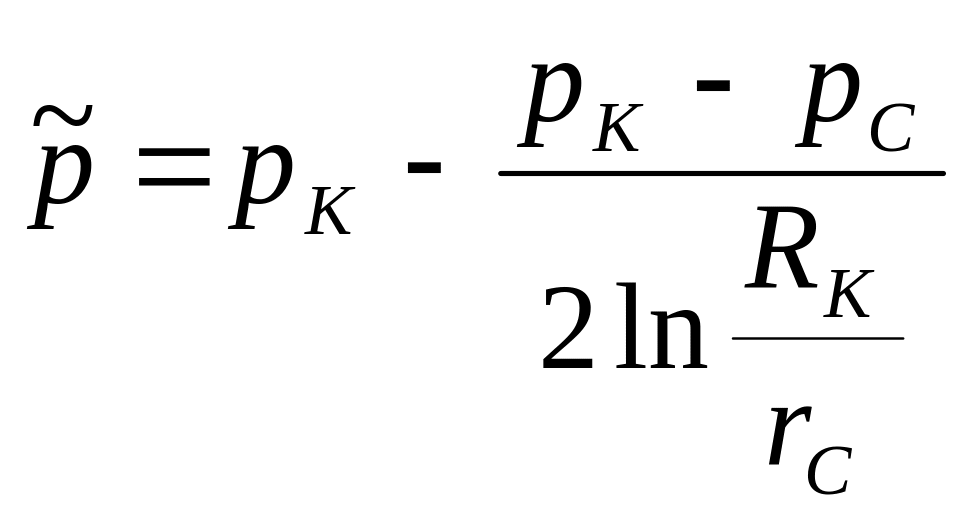
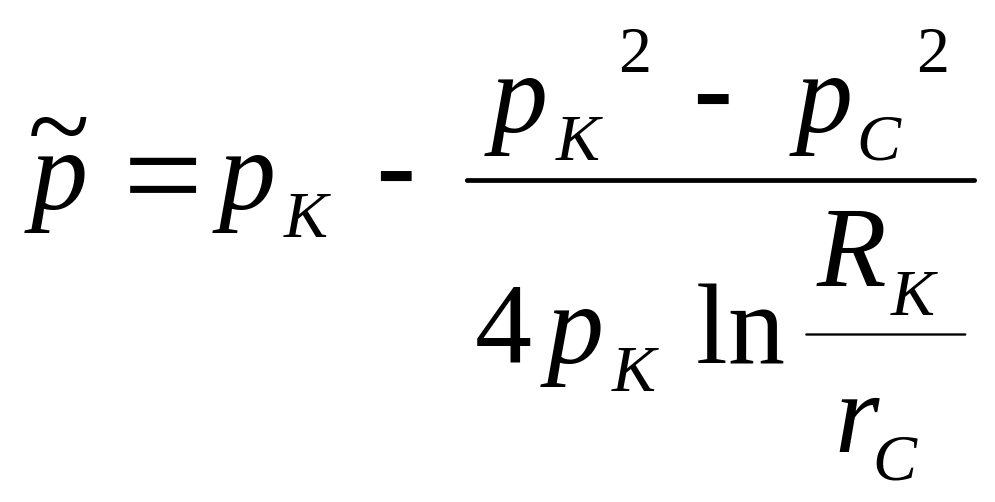
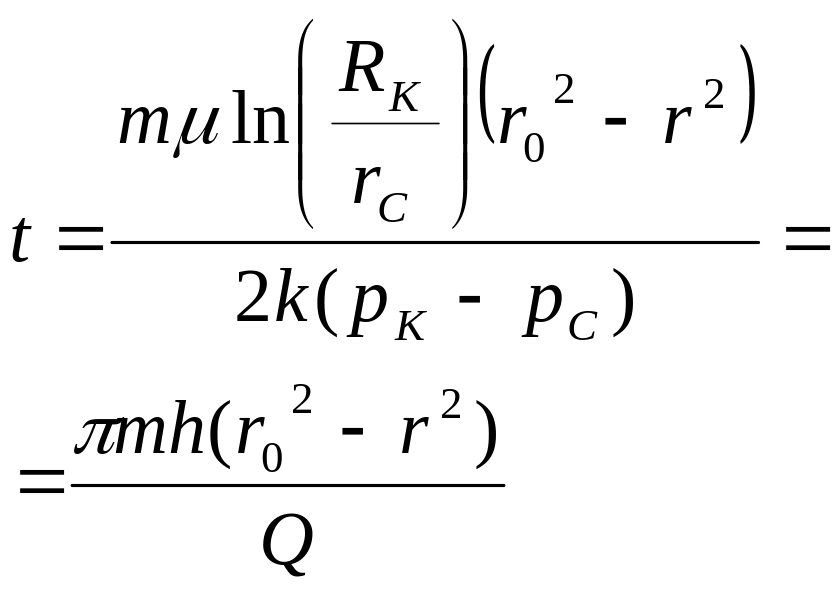
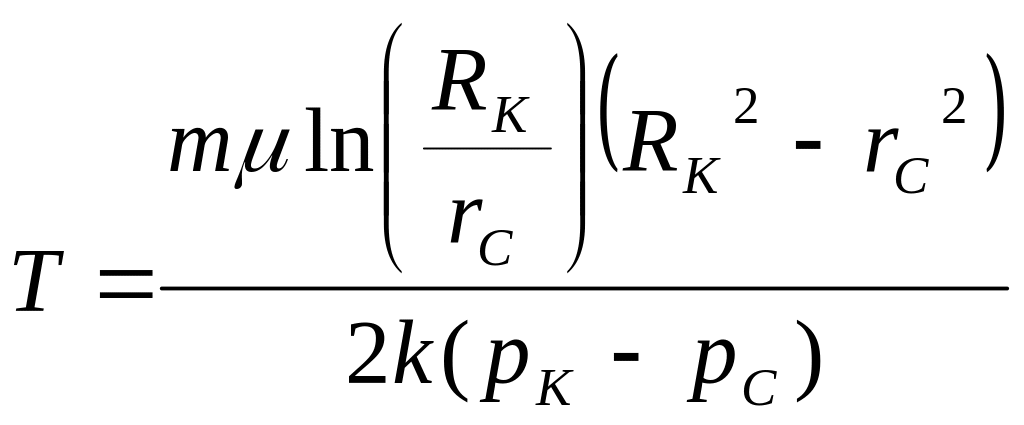
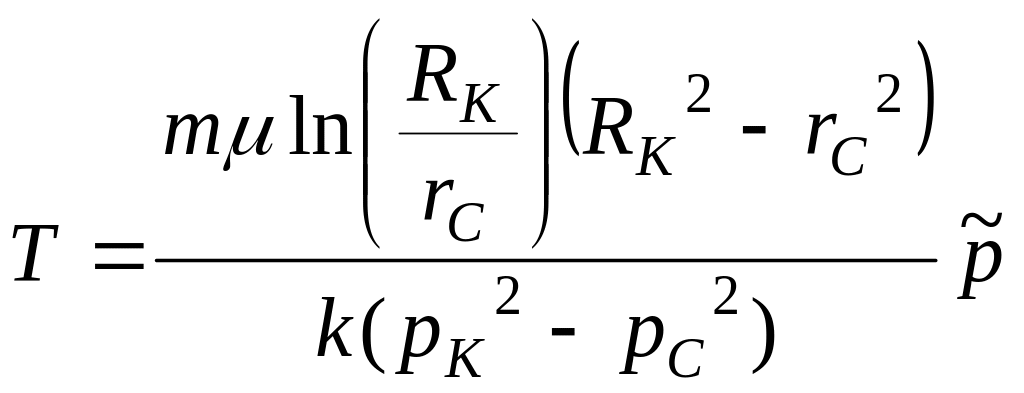
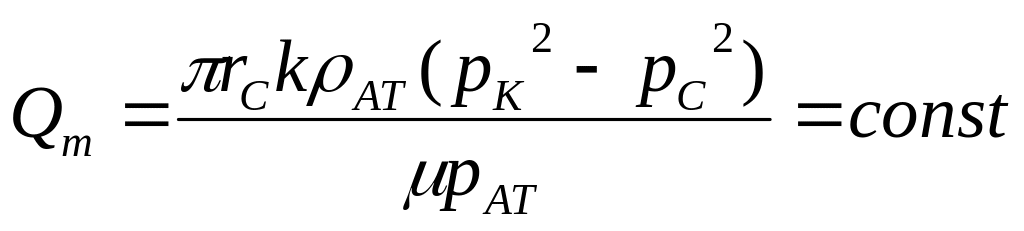
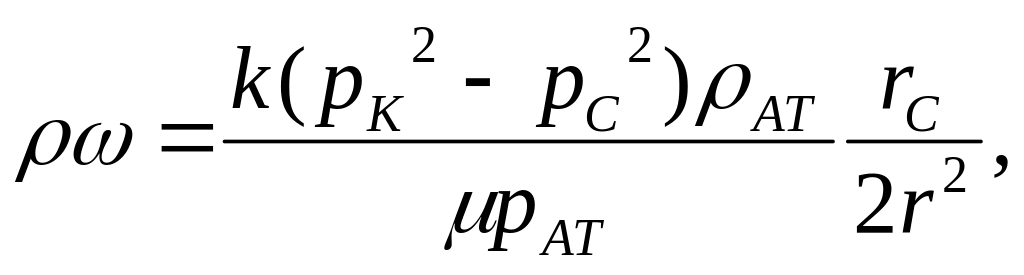
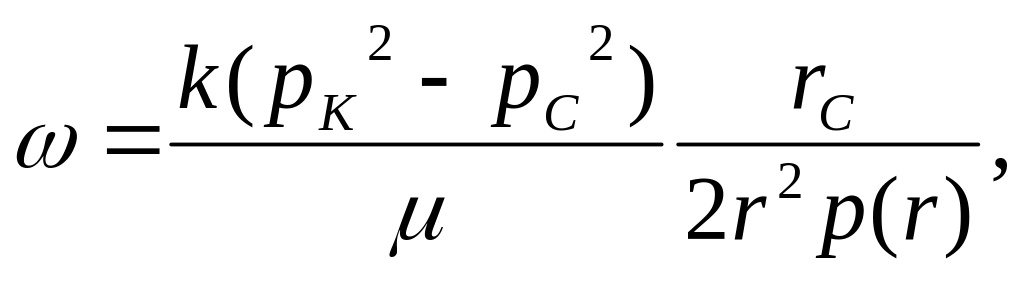
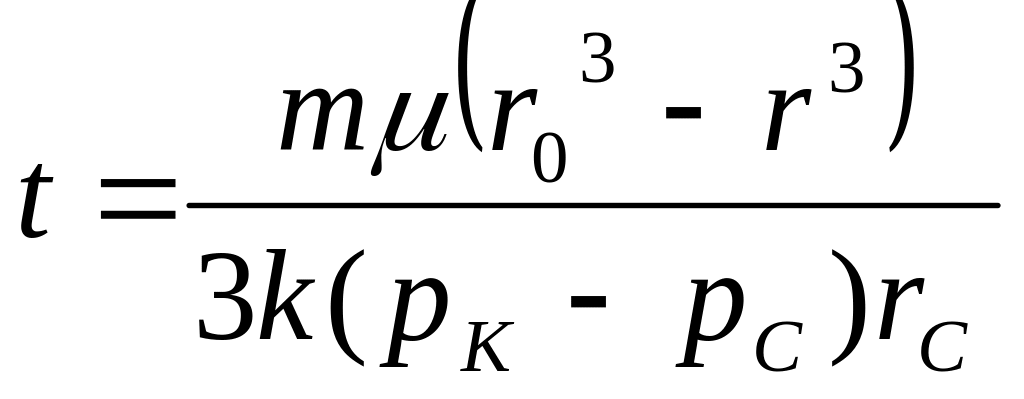
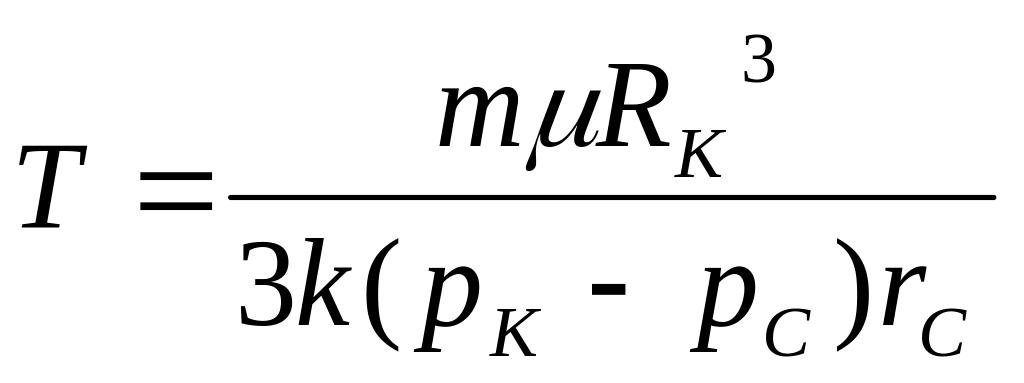
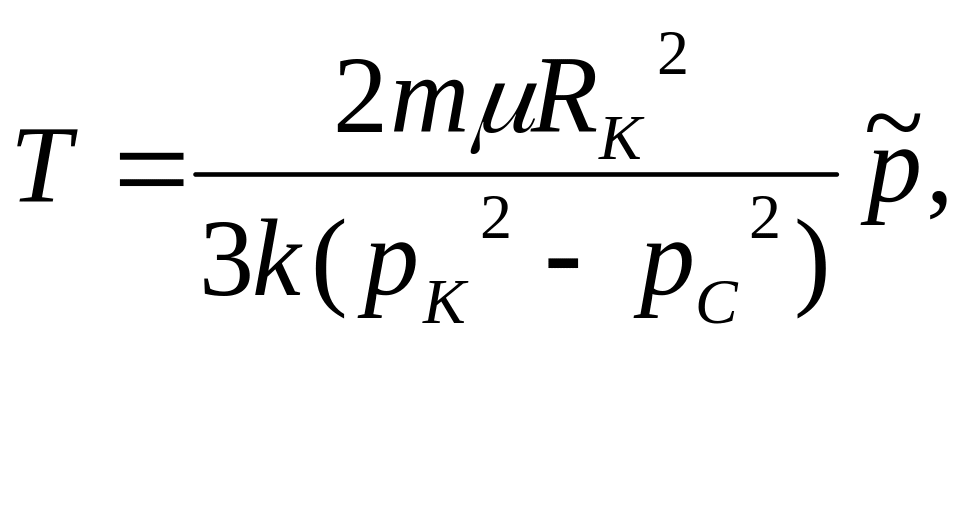 где
где