Значение коэффициента α для расчета дополнительных напряжений в грунте основания.
Для промежуточных значений ξ и η коэффициент α определяется
интерполяцией.
ξ=2z/b |
η=1/b |
||||||
1,0 |
1,4 |
1,8 |
2,4 |
3,2 |
5 |
≥10 |
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
0,0 0,4 0,8 |
1,000 0,960 0,800 |
1,000 0,972 0,848 |
1,000 0,975 0,866 |
1,000 0,976 0,876 |
1,000 0,977 0,879 |
1,000 0,977 0,881 |
1,000 0,977 0,881 |
1,2 1,6 2,0 |
0,606 0,449 0,336 |
0,682 0,532 0,414 |
0,717 0,578 0,463 |
0,739 0,612 0,505 |
0,749 0,629 0,530 |
0,754 0,639 0,545 |
0,755 0,642 0,550 |
3,6 4,0 4,4 |
0,181 0,108 0,091 |
0,173 0,145 0,123 |
0,209 0,176 0,150 |
0,250 0,214 0,185 |
0,285 0,248 0,218 |
0,319 0,285 0,255 |
0,337 0,306 0,280 |
4,8 5,2 5,6 |
0,077 0,067 0,058 |
0,105 0,091 0,079 |
0,130 0,113 0,099 |
0,161 0,141 0,124 |
0,192 0,170 0,152 |
0,230 0,208 0,189 |
0,258 0,239 0,223 |
6,0 6,4 6,8 |
0,051 0,045 0,040 |
0,070 0,062 0,055 |
0,087 0,077 0,064 |
0,110 0,099 0,088 |
0,136 0,122 0,110 |
0,173 0,158 0,145 |
0,208 0,196 0,185 |
7,2 7,6 7,8 |
0,036 0,032 0,029 |
0,049 0,044 0,040 |
0,062 0,056 0,051 |
0,080 0,072 0,066 |
0,100 0,091 0,084 |
0,133 0,123 0,113 |
0,175 0,166 0,158 |
8,4 8,8 9,2 |
0,026 0,024 0,022 |
0,037 0,033 0,031 |
0,046 0,042 0,039 |
0,060 0,055 0,051 |
0,077 0,071 0,065 |
0,105 0,098 0,091 |
0,150 0,143 0,137 |
9,6 10,0 |
0,020 0,019 |
0,028 0,026 |
0,036 0,033 |
0,047 0,043 |
0,060 0,056 |
0,085 0,079 |
0,132 0,126 |
11,0 12,0 |
0,016 0,013 |
0,021 0,018 |
0,028 0,023 |
0,036 0,031 |
0,047 0,040 |
0,067 0,058 |
0,115 0,106 |
ПРИМЕР РАСЧЕТА. Определить сжимающие напряжения под центром и под серединой длинной стороны загруженного прямоугольника размером в плане 2×8 м на глубине z=0; 0,5b; 1,0b и 2b от поверхности при внешней нагрузке интенсивностью р=0,3 МПа (3 кгс/см2).
Под центром загруженной площади η=l/b=8/2=4
z=0; |
ξ=0; |
α=1; |
σzр=0,3 Мпа; |
z=0,5b; |
ξ=2 z/b=21/2=1; |
α=0,815; |
σzр=0,244 Мпа; |
z=2 м; |
ξ=2; |
α=0,538; |
σzр=0,161 Мпа; |
z=4м; |
ξ=4; |
α=0,266; |
σzр=0,080 Мпа. |
Значения α определяются по таблице 2.1 в зависимости от параметров ξ и η1 для промежуточных значений интерполяцией.
Для точки под серединой длинной стороны прямоугольной площади загрузки, разделяем ее на два прямоугольника размером 2×4 м так, чтобы рассматриваемая точка была бы угловой. Для первого прямоугольника размером 2×4 η=l/b=4/2=2
z=0; |
ξ =0; |
α с1= α/4=0,25; |
z=0,5b=1; |
ξ =z/b=1/2=0,5; |
α с1= α/4=0,913/4=0,228; |
z=2 м; |
ξ =1; |
α с1= α/4=0,797/4=0,199; |
z=4м; |
ξ =2; |
α с1= α/4=0,477/4=0,119. |
Так как прямоугольники 1 и 2 имеют одинаковые размеры:
α с1=α с2, тогда σzс=2α с1
z=0; . |
σzс=2.0,25.0,3=0,15 Мпа; |
z=1; . |
σzс=2.0,228.0,3=0,137 Мпа; |
z=2 м; . |
σzс=2.0,199.0,3=0,119 Мпа; |
z=4м; . |
σzс=2.0,119.0,3=0,071 Мпа. |
Результаты расчета в графической форме показаны на рис. 2.3.
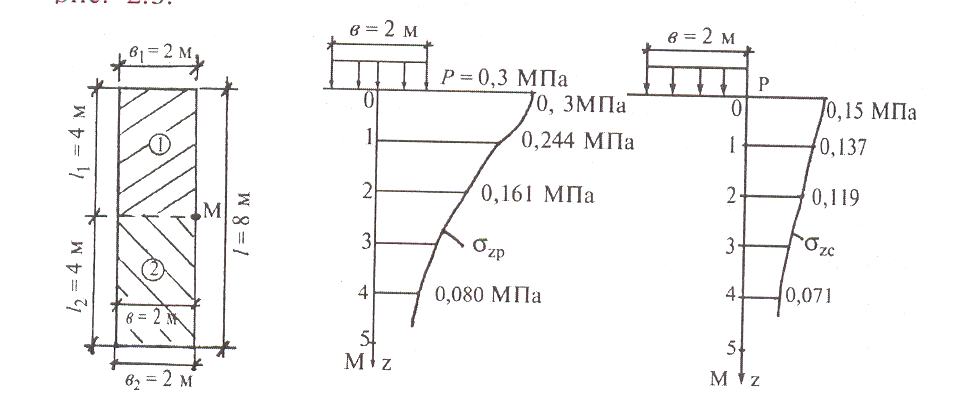
Рис.2.3. К примеру расчета определения сжимающих напряжений методом угловых точек.
Таблица 2.2.