2. Как определить опытным путем параметры источника напряжения: эдс и внутреннее сопротивление?

Чтобы опытным путём определить ЭДС источника, необходимо подключить к нему вольтметр в режиме холостого хода.

внутреннее сопротивление равно отношению напряжения холостого хода к току короткого замыкания.

3. Знать законы Ома и Кирхгофа и уметь ими пользоваться.

Закон Ома Немецкий физик Георг Ом (1787 -1854) экспериментально установил, что сила тока I, текущего по однородному металлическому проводнику (т. е. проводнику, в котором не действуют сторонние силы), пропорционально напряжению U на концах проводника: I = U/R, (1) где R - электрическое сопротивление проводника.

Если же электрическая цепь замкнута, то выбранные точки 1 и 2 совпадают, φ1 = φ2; тогда из (5) получаем закон Ома для замкнутой цепи: I =E /R, где E - э.д.с., действующая в цепи, R - суммарное сопротивление всей цепи. В общем случае R = r + R1, где r - внутреннее сопротивление источника тока, R1 - сопротивление внешней цепи. Поэтому закон Ома для замкнутой цепи будет иметь вид: I = E / (r+R1).

Первый закон Кирхгофа вытекает из закона сохранения заряда. Он состоит в том, что алгебраическая сумма токов, сходящихся в любом узле, равна нулю.

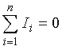
где – число токов, сходящихся в данном узле.

Второй закон Кирхгофа:алгебраическая сумма падений напряжений на отдельных участках замкнутого контура, произвольно выделенного в сложной разветвленной цепи, равна алгебраической сумме ЭДС в этом контуре

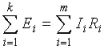
4. Знать основные методы расчета электрических цепей (метод законов Кирхгофа, МКТ, МУН, МЭГ) и уметь ими пользоваться применительно к двух-трех контурным цепям, которые будут Вам предложены при защите работы.

Провести расчет исследуемой электрической цепи (найти токи ветвей I₁, I₂, I₃) методом контурных токов (МКТ).

Для этого необходимо:

а) начертить расчетную схему (рис. 2), выделить на ней контуры и выбрать условно-положительные направления (обычно по часовой стрелке) контурных токов I_К1 и I_К2. Считать источники питания Е₁ и Е₂ идеальными источниками напряжения, т. е. пренебречь их внутренними сопротивлениями R_вт1 и R_вт2;

б) записать (составить) систему уравнений МКТ:

E1 - E2 = IK1(R1 + R2) - IK2R2,, E2 = IK2(R2 + R3) - IK1R2

(1)

или в канонической форме:

R11IK1 - R12IK2 = EK1; - R21IK1 + R22IK2 = EK2,

(2)

где R₁₁ = R₁ + R₂ и R₂₂ = R₂ + R₃ - собственные сопротивления контуров;

R₁₂ = = R₂₁ = R₂ - общее сопротивление смежных контуров; E_K1 = E₁ - E₂ и E_K2 = E₂ - контурные ЭДС;

в) подставить в систему уравнений (2) значения сопротивлений резисторов (см. п. Б) и ЭДС источников. При этом для ЭДС Е₁ следует выбрать одно из значений ряда: 10 В, 12 В, 14 В, 16 В. Выбранное значение Е₁ будет в дальнейшем использовано при проведении эксперимента (см. п. 2.4.);

г) решить систему уравнений (2), используя, например, формулы Крамера:

IK1 = 1/; IK2 = 2/,

(3)

где

	R11 -R12			EK1 -R12			R11 EK1
 =		- определитель системы;	1 =			и 2 =		-	частные определители;
	-R21 R22			EK2 R22			-R21 EK2

ПРИМЕЧАНИЕ. При расчетах все результаты следует округлять, оставляя четыре‑пять значащих цифр.

д) найти токи ветвей, пользуясь следующими правилами:

• токи в ветвях, не имеющих соседних контуров, равны соответствующим контурным токам. В нашем случае, с учетом выбранных направлений токов (см. рис. 2)

  I1 = IK1 и I3 = IK2;;

  (4)

• ток в ветви, общей для двух смежных контуров, равен разности соответствующих контурных токов. В нашем случае

I2 = IK2 - IK1;

(5)

1.2. Провести расчет исследуемой электрической цепи (найти узловое напряжение U₁₀ и токи ветвей I₁, I₂, I₃) методом узловых напряжений (МУН).

Для этого необходимо:

а) начертить расчетную схему (рис. 3), считая источники питания Е₁ и Е₂ идеальными; выбрать (заземлить) базисный узел (обычно выбирают узел, где сходится максимальное число ветвей и источников питания), например, узел 0 ;

б) направить от узла 1 к базисному узлу 0 узловое напряжение U₁₀ и записать для него уравнение

U10 = (Е1 G1 + E2 G2) / (G1 + G2 + G3),

(6)

где G₁ = 1/R₁, G₂ = 1/R₂ и G₃ = 1/R₃ - проводимости ветвей, См.

Произведения Е₁G₁ и E₂G₂ в числителе (6) берутся со знаком “+”, так как ЭДС Е₁ и Е₂ направлены к узлу 1, потенциал ₁ которого требуется определить;

Расчет сопротивления третьей ветви R₃=U₁₀/I₃

в) подставить в уравнение (6) значения проводимостей и ЭДС (см. п. 1.1, в) и вычислить узловое напряжение U₁₀ = ₁ - ₀ = ₁;

г) определить токи ветвей по обобщенному закону Ома: токи в первой и во второй ветвях (с источниками напряжений) по формулам:

I1 = (E1 - U10)G1, I2 = (E2 - U10)G2;

(7)

ток в третьей ветви, где нет источника напряжения, по формуле

I3 = U10G3;

(8)

д) занести результаты расчета электрических величин по МУН в табл. 1.

1.3. Провести расчет тока I₃ исследуемой электрической цепи методом эквивалентного генератора (МЭГ).

Для этого необходимо:

а) начертить расчетную схему, представив все элементы цепи (см. рис. 1, а) левее третьей ветви (левее зажимов 1 и 0) в виде эквивалентного генератора напряжения с ЭДС Е_ЭГ и внутренним сопротивлением R_вт (рис. 4, а).

Рис. 4

Тогда ток I₃ определяют по формуле

I3 = EЭГ / (Rвт + R3),

(9)

т. е. задача расчета заключается в определении неизвестных значений Е_ЭГ и R_вт;

б) найти ЭДС Е_ЭГ одним из методов: методом законов Кирхгофа, МКТ, МУН и др. Воспользуемся методом узловых напряжений.

Известно, что напряжение на зажимах источника напряжения при разомкнутой ветви нагрузки (режим холостого хода) равно ЭДС, т. е. U_X = E. В нашем случае (рис. 4, б) U_10X = E_ЭГ. Для расчета напряжения U_10X можно воспользоваться уравнением (6), подставив в него G₃ = 1/R₃ = 0, так как сопротивление разомкнутой ветви R₃ = . Тогда

U10X = EЭГ = (Е1G1 + E2G2) / (G1 + G2);

(10)

в) определить внутреннее сопротивление R_вт эквивалентного генератора. Для этого замкнуть (условно) накоротко источники напряжения Е₁ и Е₂ (см. рис. 1, а) перемычками и найти входное сопротивление цепи по отношению к зажимам 1 и 0 (рис. 4, в), равное R_вт,

Rвх = Rвт = R1 R2 / (R1 + R2);

(11)

г) используя полученные значения Е_ЭГ и R_вт, рассчитать по формуле (9) ток I₃;

д) занести результаты расчета электрических величин МЭГ в табл. 1.