8.Абсолютные и условные высоты. Балтийская система высот. Превышения.

Высотой точки называют расстояние по отвесной линии от точки до уровенной поверхности, принятой за начало счета высот. Если высоты отсчитывают от основной уровенной поверхности, то есть от поверхности геоида, их называют абсолютными высотами. Если за начало счета высот выбрана какая-либо другая уровенная поверхность, то высоты называют условными. В России принята Балтийская система высот. Счет абсолютных высот ведут от уровенной поверхности, проходящей через нуль Кронштадтского футштока. Разность высот двух точек называется превышением. Численное значение высоты принято называть отметкой h_AB = H_В - H_A.

9.Рельеф: основные формы, характерные точки и линии. Изображение рельефа горизонталями. Свойства горизонталей. Высота сечения, заложение, уклон.

На картах и планах рельеф изображают с помощью горизонталей, высотных отметок и условных знаков. Основными формами рельефа являются гора, котловина, хребет, лощина и седловина. Гора (возвышенность, холм, курган, сопка), Котловина (впадина), Хребет  вытянутая возвышенность, Лощина (долина, ущелье, овраг, балка), Седловина (перевал). Горизонтали  линии сечения земной поверхности равноотстоящими уровенными поверхностями. Разность h высот смежных горизонталей, равная расстоянию между секущими поверхностями, называется высотой сечения рельефа. Горизонтальное расстояние между соседними горизонталями называется заложением. Изображение рельефа горизонталями дополняется вписыванием на план отметок высот около характерных точек рельефа и специальными условными знаками, изображающими обрывы, скалы, овраги и т. п. Высоты горизонталей кратны высоте сечения рельефа. Уклоном i линии называется отношение превышения h к горизонтальному проложению d (проекция отрезка на горизонтальную плоскость – его горизонтальное проложение.)

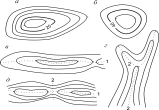
Основные формы рельефа: а – гора; б – котловина; в – хребет; г – лощина; д – седловина; 1 – водораздельная линия; 2 – водосливная линия.

10.Методы построения плановой геодезической сети: триангуляция, полигонометрия, трилатерация, линейно-угловая сеть, спутниковые методы.

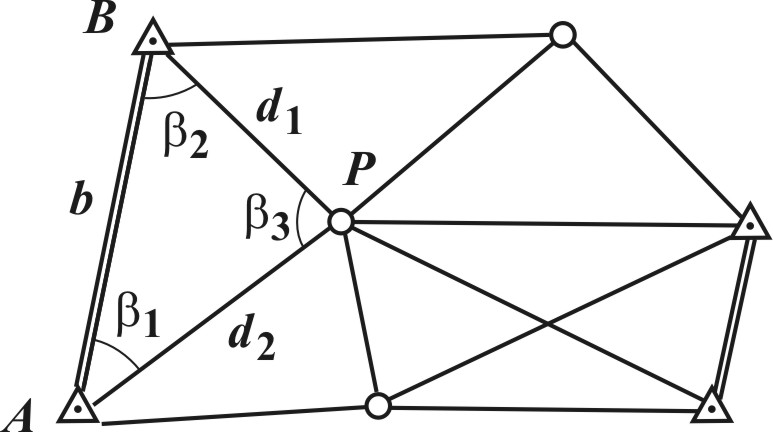
Триангуляция – метод определения планового положения геодезических пунктов путем построения на местности сети треугольников, в которых измеряют углы, а также длины некоторых сторон, называемых базисными сторонами d₁=b*sinB₁/sinB₃; d₂=b*sinB₂/sinB₃. Дирекционные углы сторон АP и ВP АВP равны a_AP=a_AB+ B₁ a_BP= a_AB+-180-B2 Координаты пункта P определятся по формулам прямой геодезической задачи Xp=Xa+d2*cosAap; Yp=Ya+d2*sinAap. Аналогично вычисляют координаты всех остальных пунктов. Трилатерация – метод определения планового положения геодезических пунктов путем построения на местности сети треугольников, в которых измеряют длины их сторон. Если в АВP известен базис b и измерены стороны BD=d_1,AP=d₂ , то на основе теоремы косинусов, можно вычислить углы треугольника;cosB1=(b^2+d2(^2)-d1(2)/2bd2; cosB2=(b^2+d1(^2)-d2(2)/2bd1; cosB3=(d1(^2)+d2(2)-b^2)/2bd1. Так же вычисляют углы всех треугольников, а затем, как и в триангуляции,  координаты всех пунктов. Линейно-угловая сеть строится, как правило, как сеть треугольников, в которых измеряют углы и длины сторон. Такие сети имеют большое число избыточных измерений и поэтому отличаются высокой надежностью. Полигонометрия  – метод определения планового положения геодезических пунктов путем проложения ломаной линии (полигонометрического хода) или системы связанных между собой ломаных линий (сети полигонометрии), в которых измеряют углы поворота и длины сторон. Схема полигонометрического хода показана на рис, где A и B – исходные пункты; CA и BD  исходные направления, дирекционные углы которых известны; 1, 2, 3, 4, 5  точки (вершины) хода;b_i  измеренные горизонтальные углы;d_i  измеренные длины сторон (i = 1, 2, …). Спутниковый метод определения координат геодезических пунктов основан на измерениях по сигналам спутников навигационных систем ГЛОНАСС (Россия) и GPS (США), выполняемых двумя (и более) наземными приемниками. По результатам измерений с высокой точностью определяют разности дX,дY,дZ геоцентрических координат между пунктами. Если координаты одного из пунктов известны, то, прибавив к ним измеренные разности, находят координаты остальных пунктов. Затем координаты преобразуют в геодезические или плоские прямоугольные.