30.Оценка точности измерений. Погрешности: средняя квадратическая, предельная, абсолютная и относительная.

Общепринятой характеристикой точности является предложенная К.Ф. Гауссом средняя квадратическая погрешность m=sqr( д^2/n), где д₁, д₂, …, д_n – случайные погрешности измерений. Достоинством этой характеристики является ее устойчивость, независимость от знаков отдельных погрешностей и усиленное влияние больших погрешностей. Средняя квадратическая погрешность определения m по формуле приближенно равна m_m=m/sqr 2n.Формула (5.4) находит применение при исследовании точности геодезических приборов и методов измерений, когда известно достаточно точное, близкое к истинному, значение X измеряемой величины. Но обычно значение измеряемой величины заранее неизвестно. Тогда вместо формулы Гаусса пользуются формулой Бесселя, определяющей среднюю квадратическую погрешность по отклонениям результатов измерений от среднего. В большинстве случаев погрешности измерений распределены по нормальному закону, установленному Гауссом. Вероятность того, что случайная погрешность превышает 2 m, равна 4,5%, а что она превышает 3 m  лишь 0,27%. Поэтому погрешности, большие 2 m, считают практически невероятными и относят к числу грубых погрешностей, промахов. Величину 2 m называют предельной погрешностью и используют как допуск при отбраковке некачественных результатов измерений. Величины д, m, д_пред, выражаемые в единицах измеряемой величины, называются абсолютными погрешностями. Наряду с абсолютными применяются также и относительные погрешности, представляющие собой отношение абсолютной погрешности к измеряемой величине. Относительную погрешность принято выражать в виде простой дроби с единицей в числителе, например m/l=1/N, где l ­ значение измеряемой величины, а N – знаменатель дроби.

31.Средняя квадратическая погрешность функций измеренных величин.

В практике геодезических измерений определяемые величины обычно являются функциями других, непосредственно измеряемых величин. Рассмотрим функцию u независимых переменных x, y, z, …u = f (x,y,z…). Продифференцируем функцию по всем переменным и заменим дифференциалы du, dx, dy, dz, …. погрешностями u, x, y, z, ….

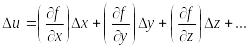Получили выражение случайной погрешности u в зависимости от случайной комбинации погрешностей x, y, z, …. Положим, что имеем n таких комбинаций, которым соответствует n выражений:

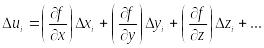(i = 1, 2, …, n)

Возведем полученные выражения в квадрат, сложим и разделим на n:

,где квадратными скобками обозначены суммы.

Устремим число комбинаций в бесконечность (n  ) и, воспользовавшись выражениями, получим: , , , , . И окончательно

Итак, квадрат средней квадратической погрешности функции общего вида равен сумме квадратов произведений частных производных по каждой переменной, умноженных на их средние квадратические погрешности.

32.Обработка прямых равноточных измерений. Арифметическая середина. Средние квадратические погрешности одного измерения и среднего арифметического.

Арифметическая средина результатов равноточных измерений. Пусть имеем результаты многократных равноточных измерений одной величины: l₁, l₂, …, l_n. Рассмотрим их среднее арифметическое

. Из (5.1) следует l_i= Х + Δ_i (i = 1, 2, … n). Поэтому напишем

= X  .

Согласно (5.2) с увеличением числа измерений сумма случайных погрешностей, деленная на их число, стремится к нулю, и, следовательно, среднее арифметическое L стремится к истинному значению Х. Поэтому значение определяемой величины принимают равным среднему арифметическому.

Средняя квадратическая погрешность арифметической средины. Пусть точность результатов измерений l₁, l₂, …, l_n характеризуется средними квадратическими погрешностями

m₁ = m₂ =  = m_n = m

и требуется найти среднюю квадратическую погрешность M арифметической средины.

Представим формулу (5.7) в следующем виде:

L = .

Среднюю квадратическую погрешность арифметической средины найдем как погрешность функции измеренных величин по формуле (5.6)

или

Формула (5.8) показывает, что погрешность арифметической средины с ростом числа измерений убывает пропорционально квадратному корню из этого числа. Так, чтобы погрешность среднего арифметического уменьшить в 2 раза, число измерений надо увеличить в 4 раза.