6. Теорема о циркуляции вектора напряжённости электростатического поля.

Итак, мы утверждаем, что циркуляция вектора   в любом электростатическом поле равна нулю, т.е.  . Это утверждение называют теоремой о циркуляции вектора  . Пусть в заданном поле с напряженностью   перемещается заряд по замкнутому пути 1а2б1. Для доказательства теоремы разобьем произвольный замкнутый путь на две части 1а2 и 2б1 (см. рисунок). Найдем работу по перемещению заряда q из точки 1 в точку 2. Так как работа в заданном поле не зависит от формы пути, то работа по перемещению заряда по пути 1а2 равна работе по перемещению заряда по пути 1б2 или  Рисунок 3.2 Из сказанного выше следует, что 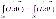(Интегралы по модулю равны, но знаки противоположны). Тогда работа по замкнутому пути:  (3) или   (4)  Поле, обладающее такими свойствами, называется потенциальным. Любое электростатическое поле является потенциальным. Теорема о циркуляции позволяет сделать ряд важных выводов, практически не прибегая к расчетам. Рассмотрим два простых примера, подтверждающих это заключение.

1. ^ Линии электростатического поля не могут быть замкнутыми. В самом деле, если это не так, и какая-то линия   – замкнута, то, взяв циркуляцию вдоль этой линии, мы сразу же придем к противоречию с теоремой о циркуляции вектора  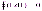:  . А в данном случае направление интегрирования в одну сторону, поэтому циркуляция вектора   не равна нулю.

2. ^ Электростатическое поле не вихревое. В ряде случаев для решения задачи о нахождении поля по известному неоднородному распределению зарядов с плотностью 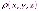 , нужны уравнения, содержащие характеристики поля в данной точке пространства или в ее малой окрестности (такое как, например, теорема Остроградского- Гаусса в дифференциальной форме). Получим такое уравнение, отражающее потенциальный характер электростатического поля. 

7. Проводники в электростатическом поле. Электростатическая индукция.

К проводникам относят вещества, у которых имеются свободные заряженные частицы, способные двигаться упорядоченно по всему объему тела под действием электрического поля. Заряды таких частиц называют свободными.  Проводниками являются металлы, некоторые химические соединения, водные растворы солей, кислот и щелочей, расплавы солей, ионизированные газы. Рассмотрим поведение в электрическом поле твердых металлических проводников. В металлах носителями свободных зарядов являются свободные электроны, называемые электронами проводимости. Если внести незаряженный металлический проводник в однородное электрическое поле, то под действием поля в проводнике возникает направленное движение свободных электронов в направлении, противоположном направлению вектора напряженности Ео этого поля. Электроны будут скапливаться на одной стороне проводника, образуя там избыточный отрицательный заряд, а их недостача на другой стороне проводника приведет к образованию там избыточного положительного заряда, т.е. в проводнике произойдет разделение зарядов. Эти нескомпенсированные разноименные заряды появляются на проводнике только под действием внешнего эл. поля, т.е. такие заряды явл. индуцированными (наведенными), а в целом проводник по-прежнему остается незаряженным.

Емкостью уединенного проводника называют физическую величину, определенную соотношением C = q/φ где q – заряд проводника, а φ – его потенциал. Емкость шара радиуса R, находящегося в вакууме, равна С = 4Пε₀R (в СИ).

Энергия электрического поля, созданного уединенным проводником, равна ½ qφ = ½ Сφ² = ½ q²/С

Емкостью конденсатора называют физическую величину, определенную отношением C = |q/U|

где q – заряд одного из проводников, образующих конденсатор, U – разность потенциалов между ними

(проводники, образующие конденсатор, несут одинаковые по величине, но противоположные по знаку заряды).

что в случае n зарядов потенциальная энергия системы равна W = ½ ∑q_iφ_i где φ - потенциал, создаваемый в той точке, где находится q_i , всеми зарядами, кроме i-го.

Если на обкладках конденсатора электроемкостью С находятся электрические заряды +q и -q, то согласно формуле напряжение между обкладками конденсатора равно U = q/С

В процессе разрядки конденсатора напряжение между его обкладками убывает прямо пропорционально заряду q от первоначального значения U до 0. Среднее значение напряжения в процессе разрядки равно U_ср = U/2 = q/2С

Для работы А, совершаемой электрическим полем при разрядке конденсатора, будем иметь: А = qU_cр = СU²/2

След, потенциальная энергия W_p конденсатора электроемкостью С, заряженного до напряжения U, равна W_p = А = qU/2

ЭЛЕКТРОСТАТИЧЕСКАЯ ИНДУКЦИЯ - появление (наведение) электрических зарядов разного знака на противоположных участках поверхности проводника или диэлектрика в электростатическом поле.Перераспределение зарядов в хорошо проводящих металлах при действии внешнего электрического поля происходит до тех пор, пока заряды внутри тела практически полностью не скомпенсируют внешнее электрическое поле. При этом на противоположных сторонах проводящего тела появятся противоположные наведённые (индуцированные) заряды. Диэлектрики в электростатическом поле поляризуются.

8. Электроёмкость проводника. Электроёмкость плоского и сферического конденсатора. Последовательное и параллельное соединение конденсаторов.

   Электроемкость проводника – это физическая величина, численно равная заряду, который необходимо сообщить проводнику, чтобы увеличить его потенциал на 1В. Диэлектрик электроемкостью не характеризуется, так как он не является эквипотенциальным телом. Электроемкость сферического конденсатора — характеристика плоского конденсатора, мера его способности накапливать электрический заряд.

   Чтобы найти емкость сферического конденсатора, который состоит из двух концентрических обкладок, разделенных сферическим слоем диэлектрика, используем формулу для разности потенциалов между двумя точками, лежащими на расстояниях r1 и r2 (r2 > r1) от центра заряженной сферической поверхности. При наличии диэлектрика между обкладками разность потенциалов будет выглядеть так:

   Подставим данное выражение в формулу электроемкости конденсатора и получим емкость конденсатора для сферического тела:

При малой величине зазора, то есть  , а следовательно можно считать, что   емкость сферического конденсатора будет равна  . Площадь сферы  следовательно формула будет совпадать с формулой емкости плоского конденсатора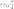 

Так же есть:

Энергия конденсатора:   

Ёмкость конденсатора :    

Ёмкость цилиндрического конденсатора :    

Емкость плоского конденсатора :    ;

В Формуле мы использовали :

 — Электроемкость сферического конденсатора

 — Относительная диэлектрическая проницаемость

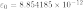 - Электрическая постоянная

 — Больший радиус (от центра, до края конденсатора)

 — Малый радиус (Его может и не быть — это пустота)