
- •15Экстремум функции нескольких переменных
- •Задание n 33
- •16Дифференциальные уравнения
- •Дифференциальные уравнения 1-го порядка с разделяющимися переменными
- •Частные решения дифференциальных уравнений 1-го порядка
- •Задание № 34
- •Однородные дифференциальные уравнения второго порядка с постоянными коэффициентами
- •Частные решения линейных однородных дифференциальных уравнений второго порядка с постоянными коэффициентами
- •Задание № 35
- •Неоднородные линейные дифференциальные уравнения второго порядка с постоянными коэффициентами (нлду)
- •Задание № 36
- •Задание n 37
- •Сходимость числовых рядов
- •Степенные ряды
- •Задание № 38
- •Задание № 39
- •Задание n 40
- •Ряд Фурье
- •18Элементы теории случайных величин
- •Задание n 41
15Экстремум функции нескольких переменных
1. Необходимые
условия.
Функция
![]() может иметь экстремум только в точках,
в которых
может иметь экстремум только в точках,
в которых
![]() и
и
![]() .
Эти точки называются критическими.
.
Эти точки называются критическими.
2. Достаточные
условия.
Обозначим через A,
C
и B
значения производных
![]() ;
;
![]() и
и
![]() в критической точке
в критической точке
![]() .
Тогда, если
.
Тогда, если
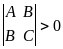 ,
то при
,
то при
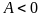 в точке
функция
имеет максимум, а при
в точке
функция
имеет максимум, а при
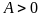 - минимум;
- минимум;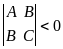 ,
то экстремума нет;
,
то экстремума нет;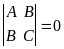 - требуется
дополнительное исследование.
- требуется
дополнительное исследование.
Пример.
Найти экстремум функции
![]() .
.
![]() ;
; ![]() .
.
Чтобы найти
критические точки решим систему
уравнений:
![]() ;
;
![]() ;
;
![]() ,
т.е. критическая точка
,
т.е. критическая точка
![]() .
.
Находим вторые частные производные:
![]() ;
; ![]() ;
; ![]() ;
;
![]() ;
; ![]() ;
; ![]() ;
;
![]() ;
;
![]() ,
следовательно, в точке
функция
,
следовательно, в точке
функция
![]() имеет минимум.
имеет минимум.
Вычислим значение
функции в точке минимума:
![]() .
.
Задание n 33
Найти экстремум:
1)
|
8)
|
15)
|
2)
|
9)
|
16)
|
3)
|
10)
|
17)
|
4)
|
11)
|
18)
|
5)
|
12)
|
19)
|
6)
|
13)
|
20) |
7)
|
14)
|
|
16Дифференциальные уравнения
Дифференциальным
уравнением называется уравнение,
связывающее независимую переменную,
искомую функцию и ее производные всех
порядков до n
включительно. Производная
второго порядка
- это производная от производной функции.
Производные третьего и более высоких
порядков определяются аналогично.
Решением
дифференциального уравнения
называется функция, которая при
подстановке в уравнение ее и всех ее
производных обращает уравнение в
тождество. В общем случае решение
дифференциального уравнения n-го
порядка содержит n
произвольных постоянных
![]() ,
,
![]() ,
...,
,
...,
![]() .
.
Дифференциальные уравнения 1-го порядка с разделяющимися переменными
При решении
дифференциальных уравнений производную
![]() принято обозначать
принято обозначать
![]() ,
т.е. производная записывается как
отношение дифференциалов. Если уравнение
может быть записано в виде
,
т.е. производная записывается как
отношение дифференциалов. Если уравнение
может быть записано в виде
![]() ,
,
то его можно
преобразовать к виду
![]() и взять от обеих частей интегралы.
Полученное при этом равенство связывает
y
и x
и является решением данного уравнения,
содержащим одну произвольную постоянную.
и взять от обеих частей интегралы.
Полученное при этом равенство связывает
y
и x
и является решением данного уравнения,
содержащим одну произвольную постоянную.
Пример.
Решить дифференциальное уравнение
![]() .
.
Решение.
![]() ;
; ![]() ;
; ![]() ;
;
![]() .
.
Частные решения дифференциальных уравнений 1-го порядка
Общее решение дифференциального уравнения 1-го порядка содержит одну произвольную постоянную. Если задано начальное условие, то эта произвольная постоянная может быть определена.
Пример.
![]() ,
, ![]() .
.
![]() ;
; ![]() ;
;
![]() Þ
Þ ![]() Þ
Þ ![]() .
.
Частное решение
имеет вид:
![]()
Задание № 34
Найти общее решение
дифференциального уравнения и частное
решение с начальным условием
![]() :
:
1)
|
2)
|
3)
|
4)
|
5)
|
6)
|
7)
|
8)
|
9)
|
10)
|
11)
|
12)
|
13)
|
14)
|
15)
|
16)
|
17)
|
18)
|
19)
|
20)
|
|
