
- •Примеры
- •Задание № 15
- •Задание n 16
- •Задание n 17
- •Задание n 18
- •Задание n 19
- •Задание № 20
- •10Применение производной для исследования функций
- •Дифференциал функции
- •Задание № 21
- •Задание n 22
- •11Интегральное исчисление
- •Свойства неопределенного интеграла
- •Определенный интеграл
- •Задание № 23
- •Задание № 24
- •Задание n 25
- •Задание n 26
- •12Геометрическое приложение определенного интеграла
- •Задание n 27
- •13Функции нескольких переменных
- •Задание № 28
- •Задание № 29
- •Задание № 30
- •14Градиент и производная по направлению
- •Задание № 31
- •Задание № 32
Свойства неопределенного интеграла
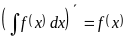 ;
;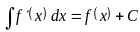 ;
;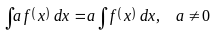 ;
;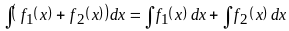 .
.
При вычислении неопределенных интегралов используются их свойства и таблица неопределенных интегралов.
Таблица основных неопределенных интегралов
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Отыскание неопределенного интеграла с помощью таблицы основных интегралов и свойств неопределенного интеграла называется непосредственным интегрированием. Кроме этого, для вычисления неопределенных интегралов применяются различные приемы. Приведем два из них.
Пусть
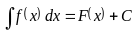 ,
тогда
,
тогда
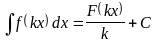 ;
;пусть
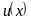 и
и
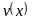 - две дифференцируемые функции, тогда
- две дифференцируемые функции, тогда
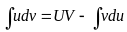 .
.
Эта формула
называется формулой
интегрирования по частям
и используется в тех случаях, когда
подынтегральное выражение
![]() можно представить в виде
можно представить в виде
![]() так, что стоящий в правой части формулы
интеграл проще, чем исходный.
так, что стоящий в правой части формулы
интеграл проще, чем исходный.
Определенный интеграл
Определенным интегралом от функции на отрезке называется выражение
![]() .
.
Определенный интеграл - это число, которое получается, если в какую-либо из первообразных функции подставить значения верхнего предела b и нижнего предела a, а затем из первого получившегося числа вычесть второе (формула Ньютона-Лейбница).
Примеры. Вычислить определенные интегралы
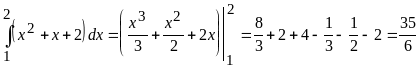 .
.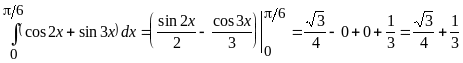 .
.
Задание № 23
Вычислить определенный интеграл.
1)
|
2)
|
3)
|
4)
|
5)
|
6)
|
7)
|
8)
|
9)
|
10)
|
11)
|
12)
|
13)
|
14)
|
15)
|
16)
|
17)
|
18)
|
19)
|
20)
|
|
Задание № 24
1)
|
2)
|
3)
|
4)
|
5)
|
6)
|
7)
|
8)
|
9)
|
10)
|
11)
|
12)
|
13)
|
14)
|
15)
|
16)
|
17) |
18) |
19)
|
20)
|
|
Задание n 25
Вычислить определенные интегралы:
1)
|
5)
|
9)
|
2)
|
6)
|
10)
|
3)
|
7)
|
11)
|
4)
|
8)
|
12)
|
13)
|
16)
|
19)
|
14)
|
17)
|
20)
|
15)
|
18)
|
|
Задание n 26
Вычислить определенный интеграл
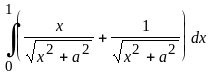 ,
,
где а - номер варианта +5.
