1) ;

2) ;

3. ;

4. ;

5. .

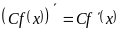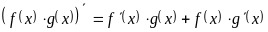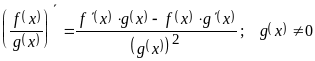II. Пусть функция имеет производную и функция имеет производную. Тогда сложная функция тоже имеет производную:

(правило дифференцирования сложной функции).

Примеры

1. ;

2. ;

3. ;

4. ;

5. ;

6. ;

7. ;

8. ;

9. ;

10. .

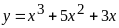
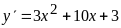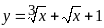
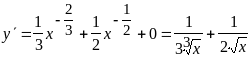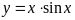
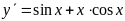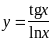
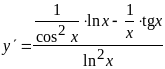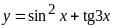
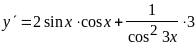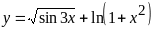
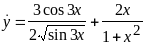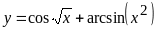
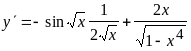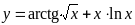
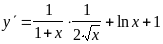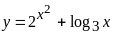
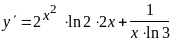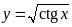
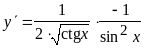Задание № 15

Найти производную

1)	2)	3)
4)	5)	6)
7)	8)	9)
10)	11)	12)
13)	14)	15)
16)	17)	18)
19)	20)

Задание n 16

Найти производную

1) 11)

2) 12)

3) 13)

4) 14)

5) 15)

6) 16)

7) 17)

8) 18)

9) 19)

10) 20)

ПРОИЗВОДНАЯ ФУНКЦИИ В ТОЧКЕ

Если функция имеет производную , то через обозначится число, получаемое, если в вычисленную производную вместо x подставить .

Примеры

1) Вычислить производную , если .

; .

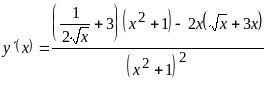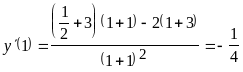2) Вычислить , если .

; .

Задание n 17

Вычислить производную , где .

1) 2) 3)

4) 5) 6)

7) 8) 9)

10) 11) 12)

13) 14) 15)

16) 17) 18)

19) 20)

Задание n 18

Вычислить :

1)	8)	15)
2)	9)	16)
3)	10)	17)
4)	11)	18)
5)	12)	19)
6)	13)	20)
7)	14)

Задание n 19

Вычислить :

1)	8)	15)
2)	9)	16)
3)	10)	17)
4)	11)	18)
5)	12)	19)
6)	13)	20)
7)	14)

Пусть функция задана параметрически в виде и , тогда производная находится по формуле

.

Производные по переменной t обозначаются также и . Тогда формула приобретает вид

.

Вторая производная от функции обозначается и является производной от первой производной, т.е.

.

Если функция задана параметрически, то вторая производная вычисляется по формуле

.

Здесь и - вторые производные по переменной t.

Задание № 20

Найти в точке .

1)		2)
3)		4)
5)		6)
7)		8)
9)		10)
11)		12)
13)		14)
15)		16)
17)		18)
19)		20)