23. Метод интегрирования по частям.

Это способ вычисления неопределенного интеграла, основанный на соотношении где u(x) и v(x) – непрерывно дифференцируемые функции, d(u(x)) и d(v(x)) – их дифференциалы.

Для вычисления определенного интеграла справедлива аналогичная формула; разница, естественно, в том, что окончание вычисления здесь – применение формулы Ньютона-Лейбница, и выбор технической детали – пересчитывать ли пределы интегрирования при замене переменной или сначала вычислить неопределенный интеграл, а затем применить формулу Ньютона-Лейбница с пределами изменения исходной переменной. Приведём эту формулу:  .

24. Свойства определенных интегралов.

I. Величина определенного интеграла не зависит от обозначения переменной интегрирования, т.е.  , где х, t – любые буквы.

II. Определенный интеграл с одинаковыми пределами интегрирования равен нулю.

III. При перестановке пределов интегрирования определенный интеграл меняет свой знак на обратный.

IV. Если промежуток интегрирования [a,b] разбит на конечное число частичных промежутков, то определенный интеграл, взятый по промежутке [a,b], равен сумме определенных интегралов, взятых по всем его частичным промежуткам.

V. Постоянный множитель можно выносить за знак определенного интеграла.

VI. Определенной интеграл от алгебраической суммы конечного числа непрерывных функций равен такой же алгебраической сумме определенных интегралов от этих функций.

25. Геометрический смысл определенных интегралов.

Если f(x) непрерывна и положительна на [a, b], то интеграл

представляет собой площадь криволинейной трапеции, ограниченной линиями y = 0, x = a, x = b, y = f(x) (см. рис. 5.).

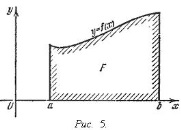
     Не следует думать, что условие непрерывности функции необходимо для того, чтобы у нее существовал определенный интеграл. Интеграл может существовать и у разрывной функции. Пусть, например, функция f(x), заданная на промежутке [a, b], равна нулю во всех точках этого промежутка, кроме конечного числа точек z₁, z₂, ..., z_N. Составим для f(x) интегральную сумму σ.

     Пусть из точек ξ₀, ξ₁, ..., ξ_n-1, входящих в определение σ, p точек совпадают с точками z_i, а остальные отличны от них. Тогда в сумме σ будет лишь p слагаемых, отличных от нуля. Если наибольшее из чисел | f(z_i) | (i = 1, 2, ..., N) есть K, то, очевидно, | σ | ≤ Kpλ ≤ KNλ,

откуда ясно, что при λ → 0 будет и σ → 0. Таким образом, интеграл

существует и равен нулю.

27. Производная от интеграла, зависящего от параметра.

О п р е д е л е н и е. Пусть функция f (x, ) двух переменных определена для всех значений х в промежутке [a, b] и всех значений   во множестве  и при каждом постоянном значении   из   функция f (x, )интегрируема в промежутке [a, b] в собственном или несобственном смысле. Тогда интеграл

является функцией переменной или параметра   и называется интегралом, зависящим от параметра.

Приведем основные свойства интеграла, зависящего от параметра:

1. В предположении, что область  представляет собой конечный промежуток [c, d], рассмотрим вопрос о непрерывности функции I ( ) (72).

Т е о р е м а 1. Если функция f(x,  ) определена и непрерывна как функция от двух переменных в прямоугольнике [a, b, c, d], то интеграл (72) будет непрерывной функцией от параметра l в промежутке [c, d].

2. Дифференцирование по параметру под знаком интеграла.

Т е о р е м а 2. Пусть функция f(x,  ) и частная производная   непрерывны в прямоугольнике  . В этом случае существует производная  , которая определяется по формуле

. Эти результаты можно обобщить. Именно: вместо интеграла (72) можно рассмотреть интеграл , (74) где g(x) является функцией абсолютно интегрируемой в промежутке [a, b] (возможно, и в несобственном смысле). Тогда при предположениях теоремы 2 о функции f(x, ) будет иметь место формула . В формуле предполагается, что пределы интегрирования a и b не зависят от параметра  . Если же a и b являются функциями  , т.е. a( ), b( ), и наряду с выполнением условий теоремы 2 существуют производные a^/( ), b^/( ), то производная интеграла (72) по параметру выражается следующей формулой:

.

3. Интегрирование по параметру под знаком интеграла.

Т е о р е м а 3. Если функция f(x,  ) непрерывна по переменным х и   в прямоугольнике  , то имеет место следующая формула:

. (77) В формуле (77) пределы интегрирования a и b не зависят от параметра  .