Вопрос 33. Промежутки монотонности функции. Необходимые и достаточные условия монотонности.

Функция   называется возрастающей на множестве  , если для любых значений аргумента   из   выполняется условие  .

Теорема 1. Если функция   имеет положительную (отрицательную) производную в каждой точке промежутка  , то   возрастает (убывает) на этом промежутке.

Теорема 2. Если функция непрерывна на промежутке   и возрастает (убывает) на промежутке  , то она возрастает (убывает) и на промежутке  .

Промежутки, на которых функция   возрастает (убывает) называются промежутками монотонности функции  .

Замечание. Функция возрастающая (убывающая) на всей области определения называетсявозрастающей (убывающей) функцией.

Замечание. Функция, возрастающая (убывающая) на каждом из нескольких промежутках не обязательно убывает на их объединении.

Теорема (достаточное условие) Если функция f(x) дифференцируема на (a,b) и f/(x)≥0  (f/(x)≤0)  на (a,b), то f(x) не убывает (не возрастает) на (a,b). Доказательство Рассмотрим случай когда f/(x)≥0 . Рассмотрим две точки x1,x2∈(a,b)  и применим формулу Лагранжа. На [x1,x2] функция f(x) удовлетворяет всем условиям этой теоремы. Следует, чтоx1<x2: f(x2)−f(x1)=f/(c)(x2−x1),  где c∈(x1,x2)  и правая часть больше нуля, значит f(x2)−f(x1)≥0  или f(x2)≥f(x1)  при x2>x1, функция не убывает. Теорема доказана. Замечание Если требовать, что f/(x)>0  (f/(x)<0) , тогда функция строго возрастает (убывает).

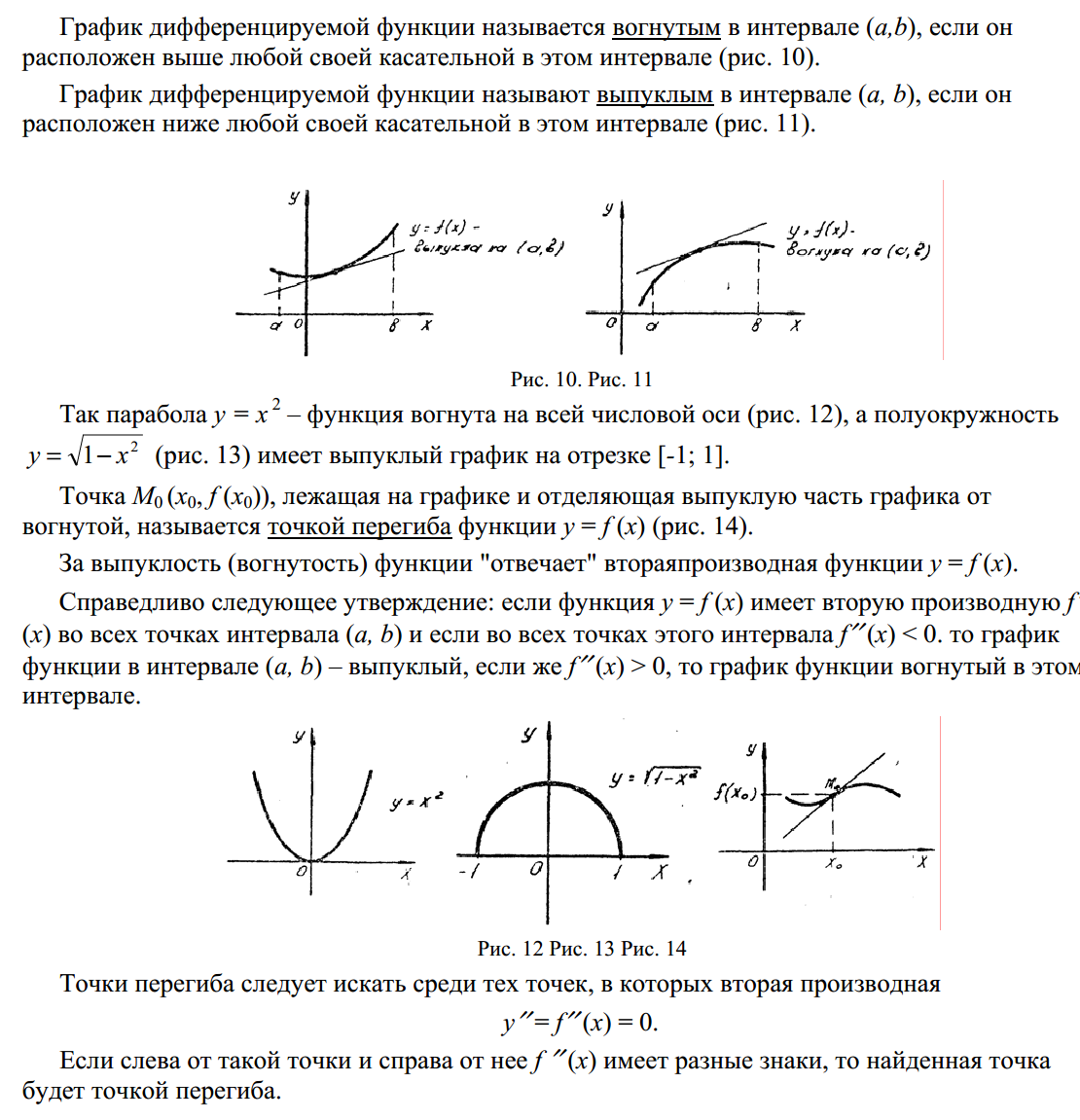
Вопрос 34. Промежутки выпуклости и точки перегиба графика функции.

Вопрос 35. Экстремумы функции. Теорема Ферма.

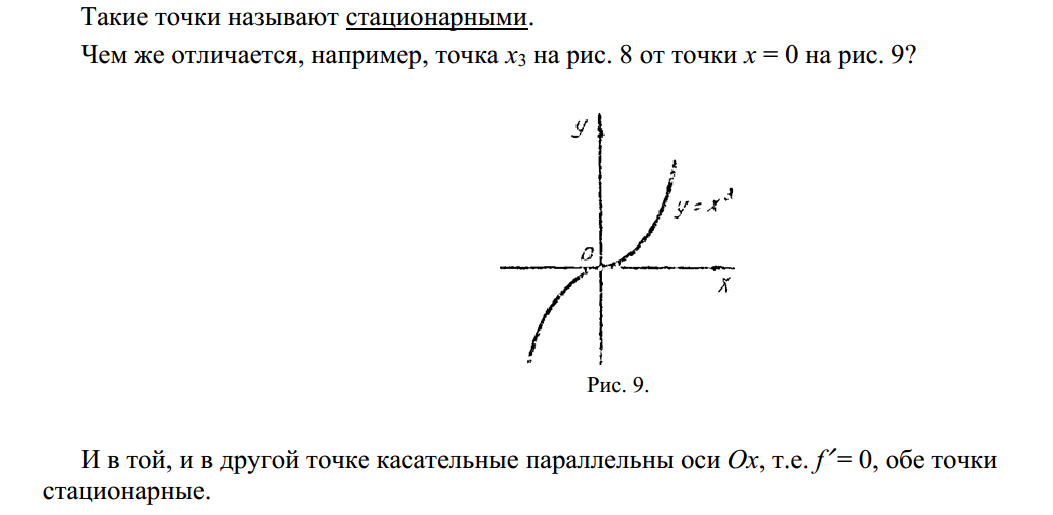
Теорема Ферма: Для любого вещественного числа 1<n≠2 уравнение xⁿ + yⁿ = zⁿ не имеет решений в вещественных, ненулевых числах x, y, z, если оно не может быть преобразовано упрощением в уравнение, не отвечающее данным условиям.                           

Вопрос 36. Асимптоты графика функции.

Вопрос 37. Пространство R^n. Множества R^n. Функции нескольких переменных

Вопрос 38. Предел и непрерывность ФНП

Величина u называется функцией нескольких независимых переменных (x, y, z, …,t), если каждой совокупности значений этих переменных ставится в соответствие определенное значение величины u. Если переменная является функцией от двух переменных х и у, то функциональную зависимость обозначают z = f (x, y). Символ f определяет здесь совокупность действий или правило для вычисления значения z по данной паре значений х и у.

Предел функции нескольких переменных. Определение: Окрестностью точки М₀(х₀, у₀) радиуса r называется совокупность всех точек (х, у), которые удовлетворяют условию  . Определение: Число А называется пределом функции f(x, y) при стремлении точки М(х, у) к точке М₀(х₀, у₀), если для каждого числа  > 0 найдется такое число r >0, что для любой точки М(х, у), для которых верно условие также верно и условие  . Записывают: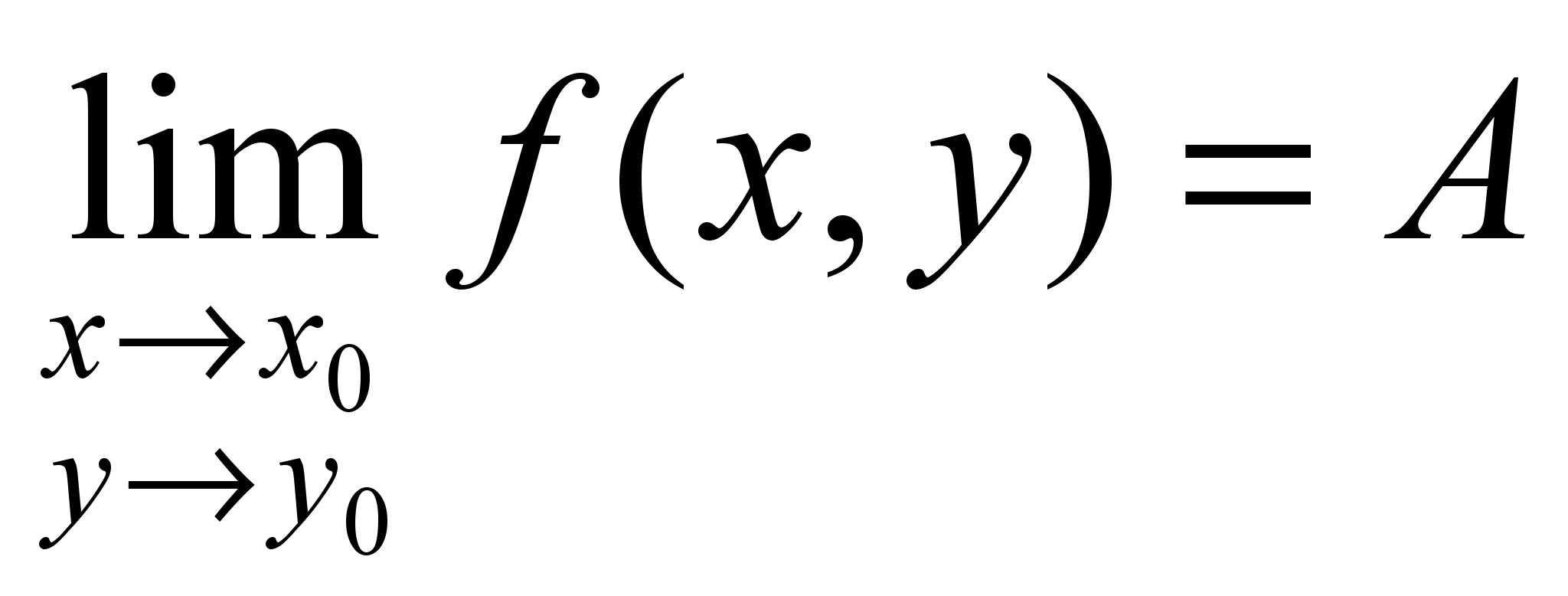 

Непрерывность функции нескольких переменных. Определение: Пусть точка М₀(х₀, у₀) принадлежит области определения функции f(x, y). Тогда функция z = f(x, y) называется непрерывной в точке М₀(х₀, у₀), если 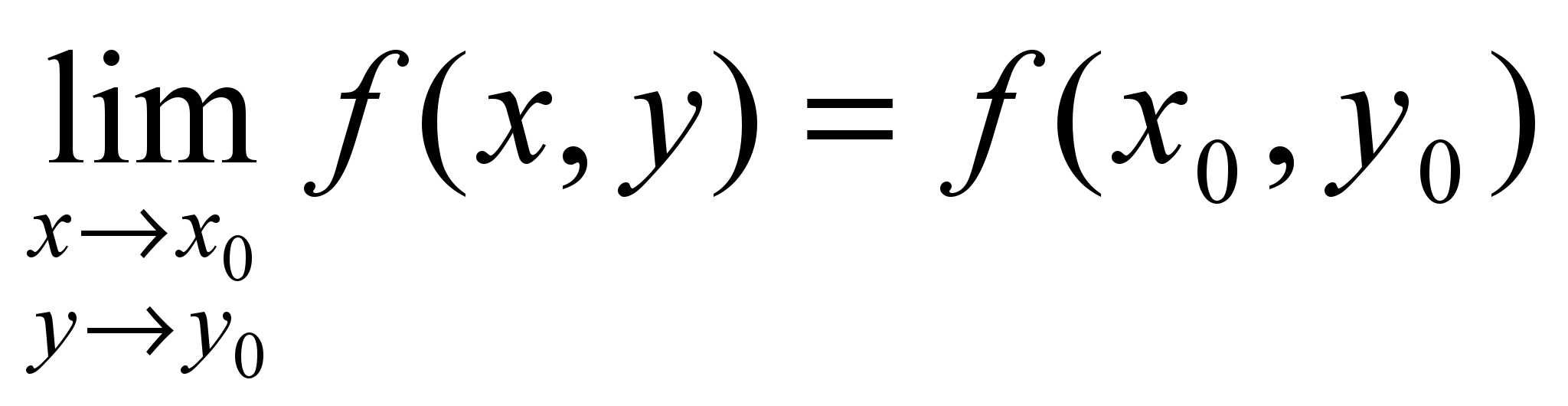  (1) причем точка М(х, у) стремится к точке М₀(х₀, у₀) произвольным образом. Если в какой – либо точке условие (1) не выполняется, то эта точка называется точкой разрыва функции f(x, y). Это может быть в следующих случаях:

1. Функция z = f(x, y) не определена в точке М₀(х₀, у₀).

2. Не существует предел  .

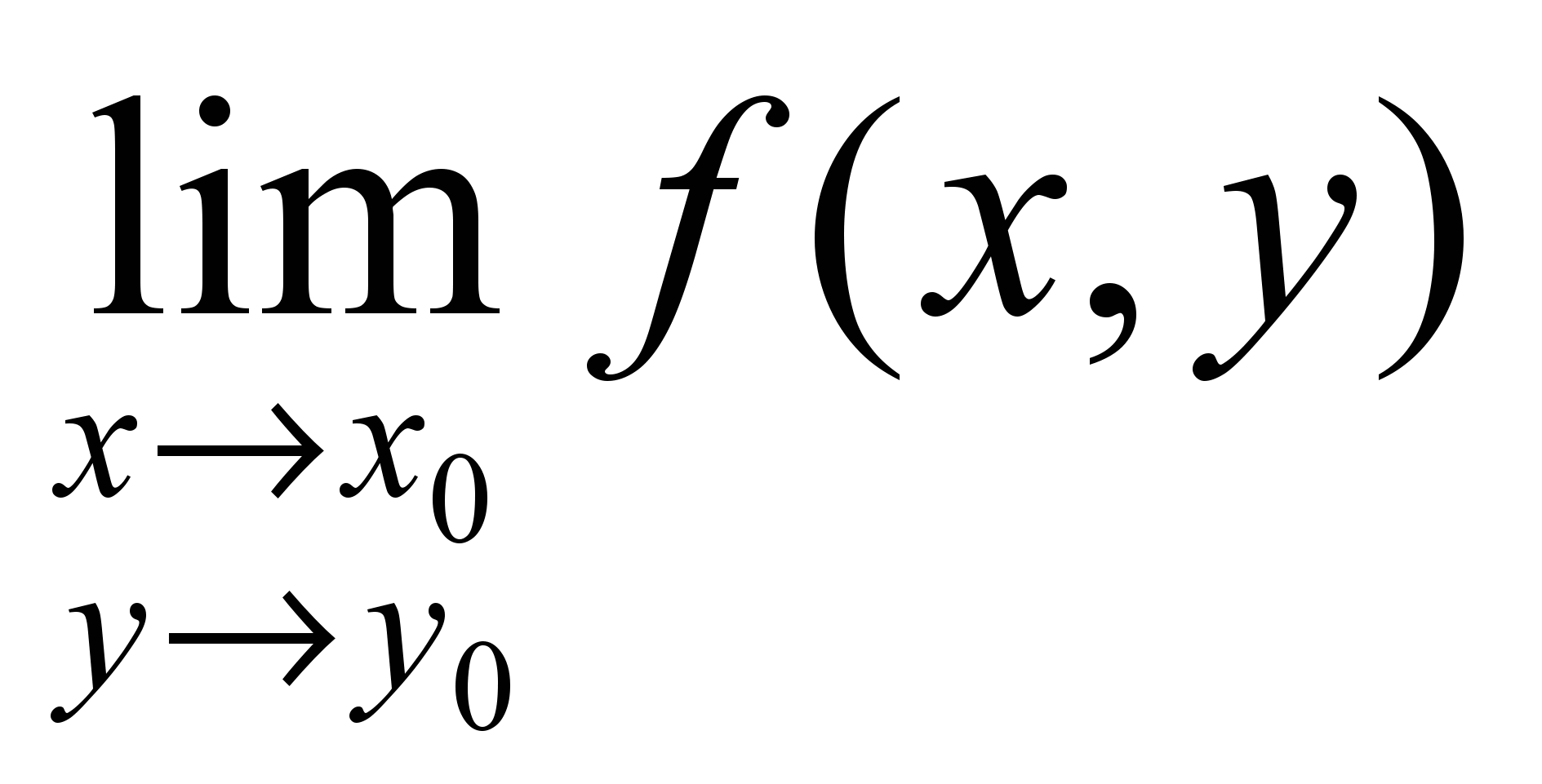3. Этот предел существует, но он не равен f( x₀, y₀).