Вопрос 29. Производные высших порядков. Механический смысл второй производной. Формула Лейбница.

Если функция   дифференцируема при всех  , то мы можем рассмотреть функцию  , сопоставляющую каждой точке   значение производной  . Эта функция  называется производной функции  , или первой производной от  . (Иногда саму исходную функцию   называют нулевой производной и обозначают тогда  .) Функция  , в свою очередь, может иметь производную во всех (или некоторых) точках   интервала  , которую мы обозначим   и назовём второй производной функции  . Если предположить, что вторая производная   существует во всех точках  , то она может также иметь производную  , называемую третьей производной функции  , и т. д. Вообще,  -й производной функции   называется производная от предыдущей,  -й производной  :

если эта производная существует.  -я производная называется также производной  -го порядка, а её номер   называется порядком производной.

При   первую, вторую и третью производные принято обозначать штрихами:   или  ; при прочих   -- числом в скобках в верхнем индексе:   или  .

Формула Лейбница-формула, выражающая производную n-го порядка (см. Дифференциальное исчисление) от произведения двух функций через производные сомножителей:

Вопрос 30. Правило Лопиталя

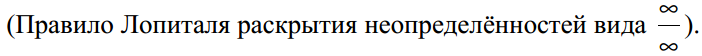
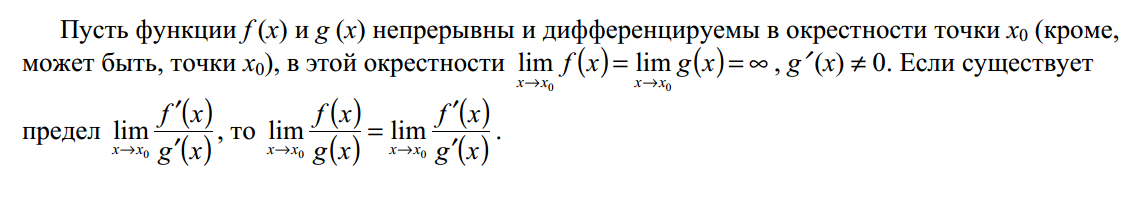
Вопрос 31. Дифференциал функции, его свойства, геометрический смысл. Инвариантность дифференциала нового порядка

Дифференциалом функции   в   называется главная, линейная относительно  , часть приращения функции.

.

Покажем, что   и   эквивалентные бесконечно малые при  :

(  - бесконечно малая).

Геометрический смысл дифференциала:

Проведем к графику функции   в точку   касательную   и рассмотрим ординату этой касательной для точки  . На рисунке ,  . Из прямоугольного треугольника   имеем:  , т.е.  . Но, согласно геометрическому смыслу производной,  . Поэтому   или  . Это означает, что дифференциал функции   в   равен приращению ординаты касательной к графику функции в этой точке, когда   получает приращение  .

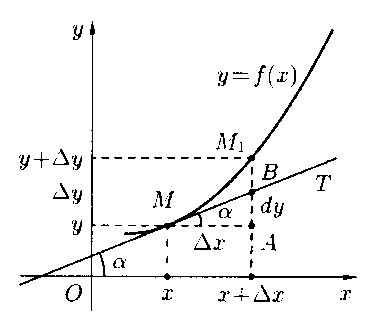
Приближенные вычисления:

Инвариантность формы записи первого дифференциала.

Пусть y=f((x))- дифференцируема в т. х₀, тогда       

                  y'_x(х₀)=f'_(U₀)'_x(x₀).

Значит

 df(х₀)=y'_x(x₀)dx=f'_(U₀)'_x(х₀)dx=f'_d=f'_(U₀)d.

Форма записи дифференциала первого порядка в зависимых и независимых переменных имеет один и тот же вид, т. е. форма является инвариантом.

Вопрос 32. Теорема Ролля. Теорема Лагранжа. Теорема Коши

Теорема Ролля

Пусть функция f: [a, b] → R непрерывна на сегменте [a, b], и имеет конечную или бесконечную производную внутри этого сегмента. Пусть, кроме того, f(a) = f(b). Тогда внутри сегмента [a, b] найдется точка ξ такая, что f'(ξ) = 0.

Теорема Лагранжа

Если функция f: [a, b] → R непрерывна на сегменте [a, b] и имеет конечную или бесконечную производную во внутренних точках этого сегмента, то   такое, что f(b) - f(a) = f'(ξ)(b - a).

Теорема Коши

Если каждая из функций f и g непрерывна на [a, b] и имеет конечную или бесконечную производную на ]a, b[ и если, кроме того, производнаяg'(x) ≠ 0 на ]a, b[, то   такое, что справедлива формула

Если дополнительно потребовать, чтобы g(a) ≠ g(b), то условие g'(x) ≠ 0 можно заменить менее жестким: