Свойства операций над множествами

Свойства перестановочности

A ∪ B = B ∪ A A ∩ B = B ∩ A

Сочетательное свойство

(A ∪ B) ∪ C = A ∪ (B ∪ C) (A ∩ B) ∩ C = A ∩ (B ∩ C)

Вопрос 18. Числовые множества. Окрестность

Числовые множества- множества, элементами которых являются числа. Примерами числовых множеств являются:

а)     множество всех натуральных чисел ( );

б)    множество всех положительных рациональных чисел ( );

в)     множество всех рациональных чисел( );

г)     множество всех целых чисел ( );

д)    множество всех чисел, удовлетворяющих неравенству  ;

Вопрос 19. Предел последовательности. Теорема о единственности предела.

В математике пределом последовательности называют объект, к которому члены последовательности в некотором смысле стремятся или приближаются с ростом номера

Теорема (о единственности предела). Если   — предел последовательности   и   — предел последовательности  , то  .

Доказательство. Предположим, что  . Возьмем  . Найдется такой номер  , что 

также существует 

Возьмем  , которое больше   и  . Тогда

Вопрос 20.Ограниченность сходящейся последовательности. Теорема Вейерштрасса

Существует три определения сходящейся последовательности :

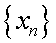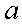1. Последовательность   называется сходящейся, если существует число   такое, что

последовательность  является бесконечно малой. При этом число   называется пределом последовательности.

2. Последовательность   называется сходящейся, если существует такое число  , что для любого   можно указать такой номер 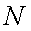 , что при всех 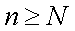  выполняется соотношение 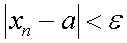 . При этом число  называется пределом последовательности.

3. Последовательность   называется сходящейся, если существует такое число  , что в любой 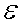 -окрестности точки  находятся все элементы последовательности, начиная с некоторого номера.

Обозначают предел последовательности: 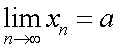  (читается «предел икс энтое при эн, стремящемся к бесконечности»), или   при  .Из определения следует, что всякая бесконечно малая последовательность является сходящейся, а ее предел равен нулю. Не представляет труда графически изобразить сходящуюся последовательность аналогично тому как мы это делали для бесконечно малой последовательности, с той лишь разницей, что нужно говорить уже не об  -окрестности нуля, а об  -окрестности точки  . Теорема (Вейерштрасс). Любая монотонная ограниченная последовательность имеет предел.

Доказательство. Докажем теорему для монотонной возрастающей последовательности  . Докажем, что точная верхняя граница для последовательности   и будет ее пределом.

Действительно, по определению точной верхней границы

Кроме того, какое бы ни взять число  , найдется такой номер  , что

Так как последовательность монотонна, то при   будет  , а значит, и   и выполняются неравенства

откуда и следует, что  .

Вопрос 21.Предел функции в точке и на бесконечности. Свойства пределов функции

Число А называется пределом функции   в точке x=х₀ (или при ), если для любой сходящейся к х₀ последовательности (1) значении аргумента x, отличных от х₀, соответствующая последовательность (2) значений функции сходится к числу А. Обозначается  . Функция   может иметь в точке х₀ только один предел. Это следует из того, что последовательность  имеет только один предел.

Число А называется пределом функции   в точке х=х₀, если для любого числа существует число  такое, что для всех  , удовлетворяющих неравенству  , выполняется неравенство  .