Вопрос 1.Определители 2-го и 3-го порядка. Свойства определителей

Определитель 2-го порядка матрицы А определяется по формуле:

Определитель 3-го порядка матрицы А определяется по формуле:

=

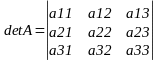Свойства определителя

1. Определитель матрицы A равен определителю транспонированной матрицы

2. Если две строки(столбца) определителя поменять местами, то определитель изменит знак.

3. Если две строки(столбца) матрицы пропорциональны или равны, то определитель равен нулю.

4. Если какую-либо строку(столбец) определителя умножить на произвольное число, то и весь определитель умножится на это число(т.е. общий множитель строки(столбца) можно выносить за знак определителя), например,

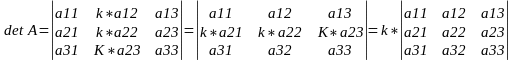
5. Если все элементы некоторой строки(столбца)равны нулю, то определитель равен нулю.

6. Определитель произведения матриц равен произведению их определителей, т.е.

7. Если к элементам некоторой строки(столбца) определителя прибавить соответствующие элементы какой-либо другой строки(столбца), умноженные на произвольное число, то определитель не изменится. Например,

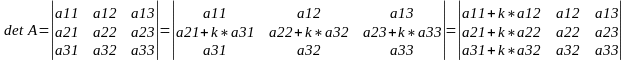
8. Определитель треугольной матрицы равен произведению элементов, стоящих на главной диагонали, т.е.

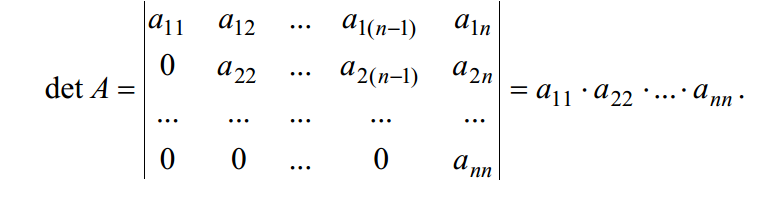
Вопрос 2.Матрицы и операции над ними. Обратная матрица. Ранг матрицы.

Вопрос 3.Системы линейных уравнений (постановка задачи). Исследование системы на совместность. Теорема Кронекера- Капелли

Теорема Кронекера- Капелли:

Вопрос 4. Однородные системы линейных уравнений. Фундаментальная система решений однородной системы.

Вопрос 5. Декартова прямоугольная система координат. Проекция вектора на ось. Координаты вектора. Орт- вектора. Направляющие косинусы.

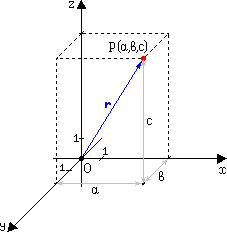
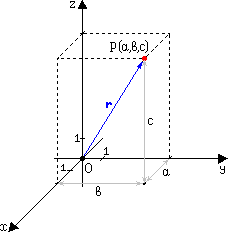
Для задания декартовой прямоугольной системы координат нужно выбрать несколько взаимноперпендикулярных прямых, называемых осями. Точка пересечения осей O называется началом координат. На каждой оси нужно задать положительное направление и выбрать единицу масштаба. Координаты точки P считаются положительными или отрицательными в зависимости от того, на какую полуось попадает проекция точки P. Д екартовыми прямоугольными координатами точки P на плоскости называются взятые с определенным знаком расстояния (выраженные в единицах масштаба) этой точки до двух взаимно перпендикулярных прямых - осей координат или, что то же, проекции радиус-вектора rточки P на две взаимно перпендикулярные координатные оси. Когда говорят про двухмерную систему коодинат, горизонтальную ось называют осью абсцисс (осью Ox), вертикальную ось - осьюординат (осью Оy). Положительные направления выбирают на оси Ox - вправо, на оси Oy - вверх. Координаты x и y называются соответственно абсциссой и ординатой точки. Запись P(a,b) означает, что точка P на плоскости имеет абсциссу a и ординату b. Декартовыми прямоугольными координатами точки P в трехмерном пространстве называются взятые с определенным знаком расстояния (выраженные в единицах масштаба) этой точки до трех взаимно перпендикулярных координатных плоскостей или, что то же, проекции радиус-вектора r точки P на три взаимно перпендикулярные координатные оси. В зависимости от взаимного расположения положительных направлений координатных осей возможны левая и правая координатные системы. Рис. 3а: Левые координатные системы Рис. 3б: Правые координатные системы Как правило, пользуются правой координатной системой. Положительные направления выбирают: на оси Ox - на наблюдателя; на оси Oy - вправо; на оси Oz - вверх. Координаты x, y, z называются соответственно абсциссой, ординатой и аппликатой. Координатными поверхностями, для которых одна из координат остается постоянной, здесь являются плоскости, параллельные координатным плоскостям, а координатными линиями, вдоль которых меняется только одна координата, - прямые, параллельные координатным осям. Координатные поверхности пересекаются по координатным линиям. Запись P(a,b,c) означает, что точка Q имеет абсциссу a, ординату b и аппликату c.

Проекция вектора на ось – это вектор, началом и концом которого являются соответственно проекции начала и конца заданного вектора.

Проекцию вектора   на ось L обозначают как  .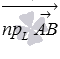

Чтобы построить проекцию вектора   на ось L, нужно из точек А и В опустить перпендикуляры на направленную прямую L – основания этих перпендикуляров дадут начало и конец искомой проекции  .

Координатами вектора называются коэффициенты его разложения по базисным векторам.

Два вектора   и   евклидова пространства называются ортогональными (перпендикулярными), если их скалярное произведение равно нулю:  .

Система векторов   называется ортогональной, если все ее векторы попарно ортогональны, т.е.   при  . Система векторов   называется ортонормированной, если все ее векторы попарно Ортогональны и длина (норма) каждого вектора системы равна единице, т.е.

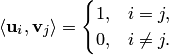
Говорят, что вектор   ортогонален (перпендикулярен) множеству  , если он ортогонален каждому вектору из  . Ортогональность векторов обозначается знаком перпендикуляра  .

Свойства ортогональных векторов

1. Нулевой вектор ортогонален каждому вектору пространства.

2. Взаимно ортогональные ненулевые векторы линейно независимы.

В самом деле, пусть векторы   попарно ортогональны. Составим из них линейную комбинацию и приравняем ее нулевому вектору:

Умножим обе части равенства скалярно на вектор 

Следовательно,  . Так как  , то  . Аналогично доказываем, что  , т.е рассматриваемая линейная комбинация тривиальная. Значит, ортогональная система векторов   линейно независима.

3. Если сумма взаимно ортогональных векторов равна нулевому вектору, то каждое из слагаемых равно нулевому вектору.

4. Если вектор   ортогонален каждому вектору системы  , то он также ортогонален и любой их линейной комбинации. Другими словами, если  , то  .

5. Если вектор   ортогонален подмножеству   евклидова пространства, то он ортогонален и линейной оболочке этого подмножества, т.e.  .

6. Если   — ортогональная система векторов, то

Это утверждение является обобщением теоремы Пифагора.

Направляющие косинусы вектора  a – это косинусы углов, которые вектор образует с положительными полуосями координат.

Чтобы найти направляющие косинусы вектора a  необходимо соответствующие координаты вектора поделить на модуль вектора.

Свойство: Сумма квадратов направляющих косинусов равна единице.

Так в случае плоской задачи направляющие косинусы вектора 

a = {a_x;a_y} находятся по формулам

Так в случае пространственной задачи направляющие косинусы вектора 

a = {a_x; a_y;a_z} находятся по формулам

Вопрос 6.Скалярное произведение векторов и его свойства

Вопрос 7.Векторное произведение векторов и его свойства

Вопрос 8.Смешанное произведение векторов и его свойства.

Вопрос 9. Уравнение плоскости

Вопрос 10. Взаимное расположение плоскостей. Угол между плоскостями.

Вопрос 11. Уравнения прямой в R³ (векторное, общее, параметрическое, каноническое)

Вопрос 12. Взаимное расположение прямых в пространстве

Вопрос 13. Угол между прямой и плоскостью. Пересечение между прямой и плоскостью.

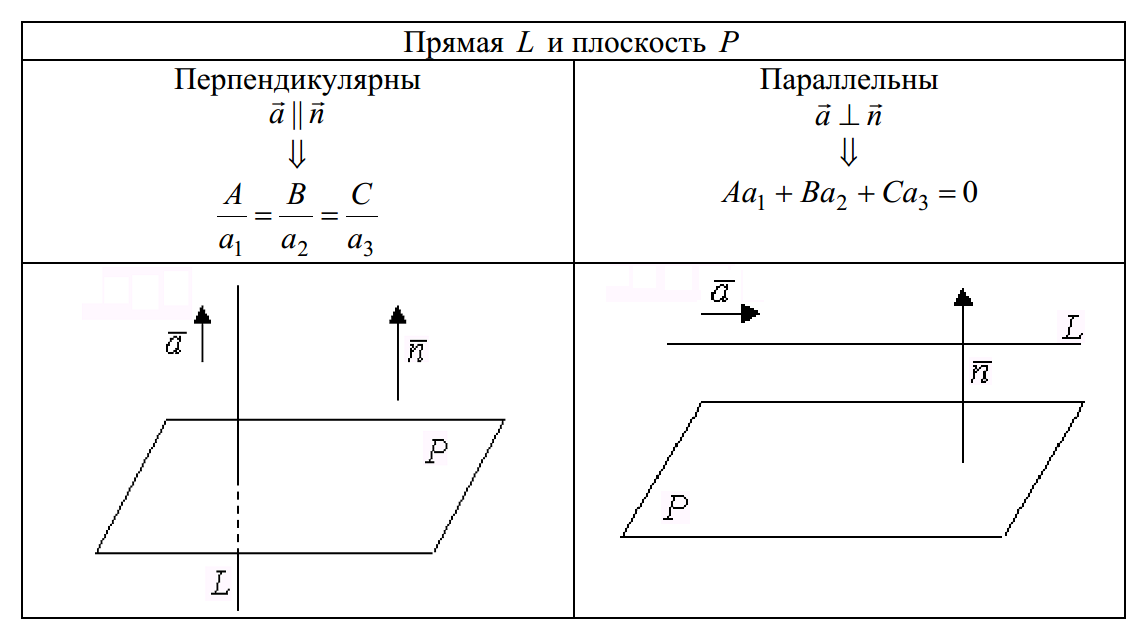
Вопрос 14. Линии второго порядка на плоскости (окружность, парабола)

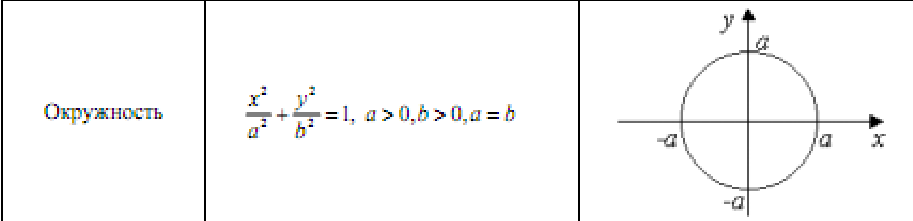
Вопрос 15. Линии второго порядка на плоскости (эллипс, гипербола)

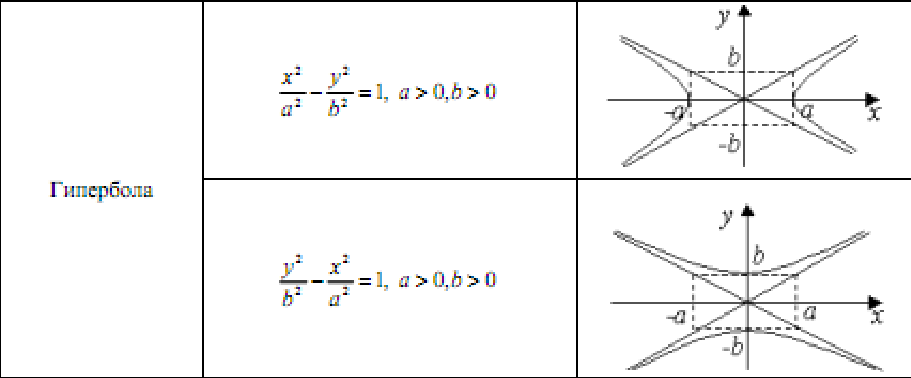
Вопрос 16. Поверхности второго порядка в пространстве. Метод сечений.

Определение. Поверхностью второго порядка называется множество всех точек пространства, координаты которых в какой-либо аффинной системе координат удовлетворяют алгебраическому уравнению второй степени:

                          ,                                                      (1)

где  a11,а22,…а00 – действительные числа, причем не все коэффициенты при членах второй степени равны нулю.

В изучении поверхностей второго порядка мы не будем исследовать уравнение (1) поверхности, а рассмотрим основные типы поверхностей, используя их простейшие (канонические) уравнения.

При этом мы будем использовать метод сечений, сущность которого состоит в следующем.

Пусть поверхность S задана в прямоугольной системе координат уравнением F(x,y,z)=0. Поверхность S пересекаем плоскостями, параллельными координатным плоскостям (или самими координатными плоскостями), и находим линии пересечения поверхности с этими плоскостями. По виду этих линий и выносится суждение о форме поверхности S. Применение метода сечений основано на следующей теореме.

Пусть в прямоугольной системе координат  заданы поверхность S уравнением (1) и плоскость , параллельная плоскости    или совпадающая с ней,  уравнением z = h. Если поверхность S пересекается с плоскостью  по линии ,  то проекция линии  на плоскость   в системе координат  имеет уравнение