
- •1.Биохимические методы очистки сточных вод. Анаэробные методы биохимической очистки.
- •2.Биохимические методы очистки сточных вод. Аэробные методы очистки сточных вод.
- •3.Биохимические методы очистки сточных вод. Общие положения. Закономерности распада органических веществ.
- •4.Гидросфера. Распространение воды в природе. Потребление воды. Свойства воды. Характеристика природных вод. Сточные воды.
- •5.Закон Кирхгофа. Взаимное излучение твердых тел.
- •6.Лучеиспускание газов. Передача тепла конвекцией.
- •7.Массопередача. Кинетика процесса абсорбции. Диф.Уравнение массообмена в движущейся среде.
- •8.Массопередача. Уравнение массоотдачи. Подобие процессов массоотдачи.
- •9.Массопередача. Фазовое равновесие. Линия равновесия. Материальный баланс. Рабочая линия. Направление массопередачи.
- •10.Механические методы очистки сточных вод. Расчет песколовок.
- •11.Обоснование допустимых выбросов при рассеивании вредных веществ через высокие источники выбросов.
- •12.Определение необходимой степени очистки производственных сточных вод.
- •13.Очистка вод коагуляцией и флокуляцией
- •14.Очистка от промышленных газовых выбросов. Общие сведенья о массопередаче. Равновесие в системе газ – жидкость.
- •15.Показатели качества сточных вод. Оценка качества сточных вод.
- •16.Понятие о системах водообеспечения (водопотребления) и водоотведения промышленных предприятий. Принципы очистки сточных вод.
- •17.Предельно допустимые выбросы вред. Вещ-в в атм. Воздух
- •18.Предельно допустимые кон-ции вред. Вещ-в в в-хе
- •19.Пылеулавливание. Параметры процесса пылеулавливания
- •20.Санитарная защита воздушного бассейна на предприятиях
- •21.Совместная очистка бытовых и промышленных сточных вод. Обработка осадков сточных вод.
- •22.Сточные воды. Удаление взвешенных примесей под действием центробежных сил.
- •23.Сухие пылеуловители. Мокрые пылеуловители.
- •2.4.3. Мокрые пылеуловители
- •24.Теоретические основы процессов осаждения твердых частиц в вязкой среде.
- •25. Тепловое излучение. Баланс теплового излучения. Закон Стефана – Больцмана.
- •26.Тепловые процессы в промышленной экологии. Температурное поле. Температурный градиент.
- •27 Теплопередача. Теплопередача при постоянных температурах теплоносителя.
- •28. Теплопроводность плоской и цилиндрической стенок
- •12.1. Теплопередача через плоскую стенку
- •29. Теплопроводность. Дифференциальное уравнение теплопроводности.
- •30.Уравнение массопередачи. Зависимость между коэффициентом массопередачи и массоотдачи. Устройство абсорбционных аппаратов.
- •31.Физико – химические методы очистки. Флотация.
- •32.Физико-химические методы очистки сточных вод. Адсорбционная очистка.
- •33.Физико-химические методы очистки сточных вод. Десорбция летучих веществ. Метод дезодорации.
- •34.Физико-химические методы очистки сточных вод. Ионообменная очистка.
- •35.Физико-химические методы очистки сточных вод. Экстракция. Обратный осмос и ультрафильтрация.
- •36.Фильтры. Процессы фильтрования. Эффективность очистки. Классификация.
- •37.Химические методы очистки сточных вод. Нейтрализация.
- •38.Электрокоагуляция. Электрофлотация. Электродиализ.
- •39.Электрофильтры. Принцип работы, расчет.
- •40.Электрохимические методы очистки сточных вод. Анодное окисление и катодное восстановление.
8.Массопередача. Уравнение массоотдачи. Подобие процессов массоотдачи.
Уравнение массоотдачи
В практических расчетах принимают, что количество вещества, переносимого в единицу времени в каждой из фаз, пропорционально разности концентраций в ядре и на границе фазы либо на границе фазы и в ядре потока.
Основное уравнение массоотдачи выражается следующим образом:
для фазы Фу
 (3.20)
(3.20)
для фазы Фx
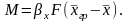 (3.21)
(3.21)
здесь
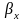 - коэффициент массоотдачи в жидкой
среде;
- коэффициент массоотдачи в жидкой
среде;
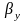 -
коэффициент массоотдачи в газовой
среде.
-
коэффициент массоотдачи в газовой
среде.
Они
показывают, какое количество вещества
переходит от поверхности раздела фаз
в ядро фазы (или в обратном направлении)
через единицу поверхности в единицу
времени при движущей силе, равной
единице. Коэффициент
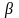 является функцией многих переменных,
т.е.
является функцией многих переменных,
т.е.
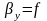 (физические
свойства среды,
(физические
свойства среды,
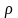 ,
,
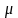 ,
геометрических параметров и др.)
,
геометрических параметров и др.)
Подобие процессов массоотдачи
Принципиальный путь для определения коэффициентов массоотдачи заключается в интегрировании уравнения диффузии в движущейся среде (3.19) совместно с уравнениями движения Навье-Стокса и уравнением неразрывности потока при заданных начальных и граничных условиях. Однако система указанных уравнений практически не имеет общего решения. В этом случае на основе теории подобия можно найти связь между переменными, характеризующими процесс переноса в потоке фазы, в виде критериального уравнения массоотдачи.
Подобие граничных условий можно установить, допуская наличие пограничного слоя, в котором перенос осуществляется только молекулярной диффузией. Количество вещества, переходящего из ядра фазы Фу к границе фазы Фx (рисунок 3.5), в соответствии с уравнением (3.20) составляет:

То
же количество вещества переносится
молекулярной диффузией через пограничный
слой при
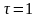
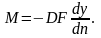
Приравняв эти два выражения, найдем зависимость, характеризующую подобие условий переноса на границе фазы:
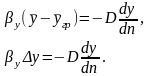
Учитывая,
что для подобных процессов отношение
сходственных величин равно отношению
величин им пропорциональным, дифференциалы
заменим конечными разностями:
В соответствии с правилом преобразования дифференциальных уравнений разделим левую часть уравнения на его правую часть, сократим подобные члены и опусти знак «d» для подобных систем, тогда получим:
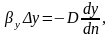
Выражение
 (3.22)
(3.22)
Комплекс
(3.22) представляет собой критерий подобия
и носит название диффузионного критерия
Нуссельта (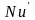 )
)
 (3.23)
(3.23)
где - мера интенсивности суммарного переноса вещества в фазе;
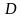 -
мера интенсивности переноса молекулярной
диффузии;
-
мера интенсивности переноса молекулярной
диффузии;
- выражает подобие переноса вещества у границы фазы в рассматриваемых системах.
Для установившегося процесса массоотдачи критерий выражается зависимостью
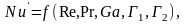 (3.24)
(3.24)
где
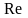 - критерий Рейнольдса;
- критерий Рейнольдса;
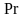 - критерий Прандтля;
- критерий Прандтля;
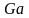 - критерий Галилея;
- критерий Галилея;
![]() - геометрические характеристики:
- геометрические характеристики:
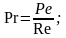
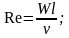
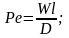
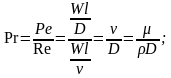
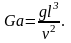
Зависимость (3.24) может быть представлена в степенной форме:

В развернутом виде можно записать:
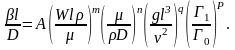 (3.25)
(3.25)
Зависимость (3.25) называется обобщенным критериальным уравнением массоотдачи.
9.Массопередача. Фазовое равновесие. Линия равновесия. Материальный баланс. Рабочая линия. Направление массопередачи.
Общие сведения о массопередаче
В процессе очистки газов широко используют процессы массопередачи, характеризуемые переходом одного или нескольких веществ из одной фазы в другую. При очистке газов в основном используют процессы массопередачи между газовой и жидкой фазами.
Поглощение газа жидкостью, т.е. процесс разделения, характеризующийся переходом вещества из газовой фазы в жидкую, называется абсорбцией. Обратный процесс, выделение газа из жидкости - десорбция. Жидкий поглотитель - абсорбент, поглощаемый газ - абсорбтив. Поглощение газа твердым пористым поглотителем, т.е. процесс разделения, характеризуемый переходом вещества из газовой фазы в твердую называется адсорбцией. Обратный процесс - десорбция, часто проводится после адсорбции с целью регенерации поглощенного вещества из поглотителя. Разновидностью адсорбции является ионный обмен - процесс разделения, основанный на способности ионитов обменивать свои подвижные ионы на ионы растворов. Если же газ (абсорбтив) образует с абсорбентом химическое соединение, то процесс называется хемосорбцией.
Массопередача происходит обычно через границу раздела соприкасающихся фаз. Перенос вещества из фазы к границе раздела фаз или в обратном направлении, т.е. в пределах одной из фаз, называется массоотдачей.
Абсорбция относится к массопередаче, в которой участвуют минимально три вещества: одно образует первую фазу, другое - вторую фазу, а третье представляет собой распределяемое между фазами вещество. Вещества, составляющие каждую из фаз, являются лишь носителями распределяемого вещества, а сами не переходят из фазы в фазу. Так, например, при поглощении аммиака водой из его смеси с воздухом вода и воздух служат носителями распределяемого вещества (аммиака). Распределяемое вещество внутри каждой фазы переносится путем диффузии, поэтому процессы массопередачи называются также диффузионными процессами. Для диффузионных процессов принимают, что количество вещества приблизительно равно поверхности раздела фаз и движущей силе. Движущую силу в процессе массопередачи выражают через разность концентраций.
Расчетные выражения движущей силы для процессов массоотдачи и массопередачи неодинаковы. Процессы массотдачи в большей части обратимы, т.е. могут протекать в противоположных направлениях в зависимости от температуры, давления и др.
Фазовое равновесие. Линия равновесия
Рассмотрим случай поглощения SO2 из смеси с воздухом чистой водой. Ввиду отсутствия равновесия, начальные условия будут следующими: концентрация SO2 = у в фазе Фy (воздух); концентрация SO2 = Х в фазе Фх (вода).
С началом растворения SO2 в воздухе начнется переход части его молекул в обратном направлении со скоростью приблизительно равной концентрации SO2 в Н2О и на границе раздела фаз, с течением времени () скорость перехода (Wп) SO2 в Н2О будет снижаться, а скорость обратного перехода будет возрастать, причем такой двусторонний переход будет продолжаться до тех пор, пока скорости переноса в обоих направлениях не станут равными друг другу. При равенстве скоростей установится динамическое равновесие, при котором не будет происходить видимого перехода вещества из фазы в фазу.
При равновесии достигается определенная зависимость между пре-дельными или равновесными концентрациями распределяемого вещества в фазах для данных температуры и давления, при которых осуществляется процесс массопередачи.
В самом общем виде связь между концентрациями распределяемого вещества в фазах при равновесии выражается зависимостью (рисунок 3.1):
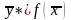 ,
(3.11)
,
(3.11)
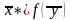 .
(3.12)
.
(3.12)
Конкретный вид закона равновесного распределения, выражающего зависимости (3.11) и (3.12), различен для разных процессов массопередачи. При низких концентрациях распределяемого вещества в исходном растворе равновесие описывается законом Генри.
Зная линию равновесия для конкретного процесса и рабочие, т.е. рав-новесные концентрации фаз в соответствующих точках, можно определить направление и движущую силу массоотдачи в любой точке аппарата. На основе этих данных может быть рассчитана средняя движущая сила, а по ней – скорость процесса массоотдачи.

а б
Рисунок 3.1 – Диаграммы равновесия:
а – при р = const и t = const; б –при р = const
Материальный баланс. Рабочая линия
В реальных условиях рабочие концентрации распределяемого вещества не равны равновесным и в действующих аппаратах никогда не достигают равновесных значений. Зависимость между рабочими концентрациями распределяемого компонента в фазах у = f (х) изображается линией, которая называется рабочей линией процесса. Вид функции можно получить из решения материального баланса.
Пусть имеется рабочий аппарат, в котором происходит процесс массопереноса ( рисунок 3.2).
Здесь Lн - жидкая фаза, кг/ с схн.(массовая доля распределяемого вещества);
Gн - газовая фаза, кг/ с с ун.(массовая доля распределяемого вещества).
Составим материальный баланс для фаз и компонентов распределяемых в аппарате в целом, следовательно, установим функцию изменения у (распределяемого вещества), т.е. изменение рабочей линии процесса массопередачи.
Материальный баланс по всему веществу определяется какGн + Lн = Gк.+ Lк. .
Материальный баланс по распределяемому веществу равен
Gнун.
+ Lнхн.
= Gк.
 + Lк.хк
.
+ Lк.хк
.
Lн,хн.
Gк,
ук




G,
у
L,
х
Gк,
ун
Lк,
,хк
Рисунок 3.2 -Противоточный массообменный аппарат
Для текущего сечения аппарата, начиная с нижнего конца, получаем:
Gн + L = G + Lк. - по всему веществу;
Gн .ун. + L .х = Lк . хк.+ G .у - по распределяемому веществу,
откуда
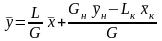 .
(3.13)
.
(3.13)
Выражение (3.13) представляет собой уравнение рабочей линии, выражающее связь между рабочими концентрациями распределяемого компонента в фазах для произвольного сечения аппарата.
Если
принять, что Lк.
= L
и Gн.=
G,
то
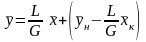 .
.
Введем
обозначения:
 ,
,
тогда у = Ах + В.
Таким образом, рабочая линия представляет собой прямую, которая наклонена к горизонту под углом, тангенс которого равен А, и отсекает на оси ординат отрезок, равный В. Рабочая линия всего аппарата ограничена точками системы координат хн.,ук. и ун.,хк.
Направление массопередачи
Распределяемое вещество всегда переходит из фазы, где его содержание выше равновесного, в фазу, в которой концентрация этого вещества ниже равновесной. Направление переноса распределяемого вещества можно определить с помощью линии равновесия и рабочей линии.
Пусть массопередача происходит между фазами Фу и Фх, а рабочие концентрации равны y иx, соответственно. При извлечении распределяемого компонента из газовой фазы рабочая линия расположена выше равновесной (рисунок 3.3). В этом случае для произвольно выбранной на рабочей линии точки А концентрация составляет:
у >у*;х < х*
.
y
у=f(х)
у*=f(х
)


уа

ун


А




у



Фу
Фх

ук.

у

ук*
x
хн
х
хк
х*
.хк*
ха
![]()
Рисунок 3.3 - Определение направления массопередачи по у-х диаграмме
