9. Элементы общей теории искажений.

Картография подразделяется на математическую картографию, картометрию, картоведение и другие разделы.

Первой ступенью в процессе создания карты является мате­матическая картография — наука о математической основе карт, способах и средствах использования карт и картографиче­ских проекций для различных измерений. Составной частью ма­тематической картографии является картометрия, изучающая способы и средства выполнения измерений по картам. Картове­дение изучает свойства и элементы карт, возможности их ис­пользования на практике, историю развития.

Изобразить земную поверхность, т. е. поверхности сферы на плоскости, сложно. Поверхность сферы не может быть разверну­та на плоскость без искажений. Почему это так? Как можно ис­следовать характер этих искажений?

В математической картографии-под развертыванием одной поверхности на другую понимают такое преобразование первой поверхности изгибанием, при котором сохраняются все элемен­ты ее внутренней геометрии, а именно углы, площади, Гауссова кривизна, а также свойство кратчайших линий оставаться крат­чайшими. Последнее свойство, по терминологии проф. В. В. Каврайского, называется ортодромичностью.

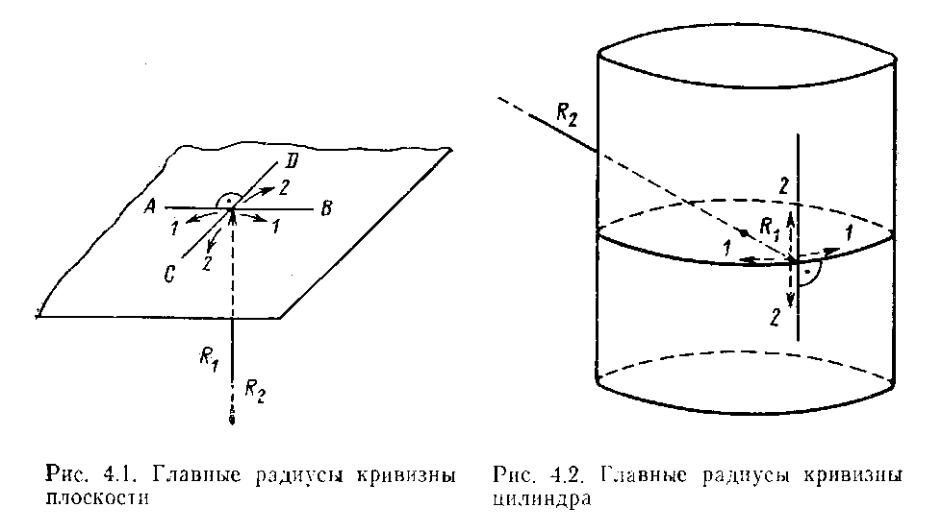
Для того чтобы понять, что такое Гауссова кривизна, необ­ходимо обратиться к дифференциальной геометрии, которая ут­верждает, что в любой точке каждой поверхности существуют два взаимно перпендикулярных нормальных сечения, имеющих наибольший и наименьший радиусы кривизны по сравнению с другими нормальными сечениями. Они называются главными радиусами кривизны в данной точке поверхности (рис. 4.1). Га­уссова кривизна k, являющаяся мерой кривизны поверхности в данной точке,

R1 и R2 – главные радиусы кривизны

Географической картой называется уменьшенное, обобщенное изображение земной поверхности на плоскости, полученное по оп­ределенному математическому закону. На основании сказанного ра­нее о невозможности развернуть шар или сфероид на плоскость ис­кажения изображений на географической карте неизбежны.

Планом называется такое изображение земной поверхности на плоскости, искажения которого не выходят за пределы графической точности, т. е. не превосходят 0,2 мм. В пределах этой точности на плане сохраняются углы, площади и свойство ортодромичности.

Картографической проекцией называется математический закон, осуществляющий связь между положением точки на земной поверх­ности и положением изображения этой точки на карте.

Гауссова кривизна шара k_m (рис. 4.4) есть величина постоян­ная, отличная от нуля:

Так как главными радиусами кривизны сфероида являются радиус кривизны меридианного сечения М и радиус кривизны сечения первого вертикала N, Гауссова кривизна сфероида

Очевидно, что эта величина переменная, зависящая от широ­ты исследуемой точки.

Сравнение формул (4.1), (4.2) и (4.3) показывает, что шар и сфероид нельзя развернуть на плоскость, а, следовательно, и на цилиндр и конус. Шар нельзя развернуть на сфероид, и нао­борот. Изобразить же шар и сфероид на плоскости можно раз­личными способами, имея в виду при этом, что будут неизбеж­ны те или иные искажения элементов внутренней геометрии. Если сохранить углы, то кратчайшие линии на шаре или сфсро- иде не будут прямыми па плоскости, т. е. не будет сохранена ортодромичность, и масштаб площадей не будет постоянным. Сохранение постоянства масштаба площадей неизбежно приве­дет к искажению углов и нарушению свойства ортодромичности.

Попытка сохранить ортодромичность вызовет искажение уг­лов и непостоянство масштаба площадей. Следовательно, на любой карте неизбежны искажения элементов внутренней гео­метрии земного сфероида. Картой (географической, навигацион­ной и т. д.), по определению проф. В. В. Каврайского, называет­ся уменьшенное, обобщенное изображение земной поверхности на плоскости, полученное по определенному математическому закону. Этот математический закон, по которому осуществляет­ся связь между положением точки на картографируемой поверх­ности и положением изображения той же точки на карте, назы­вается картографической проекцией.