4. Длины дуг параллелей и меридианов.
Подставляя значения параметров эллипсоида Красовского а и е2:
а(1-е2) А = 6 368 027,5
а(1-е2)
В = 32 073 и
значение d
= arc1
=
получим окончательно:
S = 1852,25 – 9,31 Cos2 метры (1.12)
Как видим, длина одной минуты дуги меридиана величина переменная, зависит от удвоенной широты места исследуемой точки и меняется в пределах от 1843,0 м на экваторе и до 1861,6 м на полюсе.
В навигации принято Землю принимать за шар, у которого длина одной минуты дуги меридиана равна округленной до целого значения величины 1852 метра.
Эту величину морской мили в метрах узаконили на Международном гидрографическом бюро в Монако в 1928 году.
2.4 Длина одной минуты дуги параллели
Исходя из условия кривизны любой кривой, можно записать выражение для длины 1 минуты дуги параллели:
Р = r arc1
Ранее мы нашли, что х = r, тогда вместо r подставим значение координаты х и запишем:
Р
= r
arc1
=
,
вместо arc1
и
а подставим
их значения и получим окончательно:
метр
(1.13)
Эксцентриситет
,
а е2
= 0,0066934
5.Длина одной морской мили(одной минуты дуги меридианов)
Длина одной минуты дуги меридиана.
Длина S одной минуты дуги меридиана может быть определена из следующего равенства:
d
S
= M
d
=
(1.10),
следовательно, дуга меридиана между параллелями 1 и 2 будет:
S
= a(1-e2)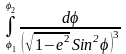
(1.11)
Этот интеграл не выражается в элементарных функциях, поэтому подынтегральное
выражение
разложим в ряд, получим:
= 1
+ 3/2e2Sin2
+ 15/8e4
Sin4
+ 105/48e6Sin6
+ ……..
Продолжим разложение значений Sin.
Sin2 = ½ - 1/2Cos2 - …………..
Sin4 = 3/8 – 1/2Cos2 + 1/8 Cos4 + ………….тогда:
= A – B Cos2 + C Cos4 - Dcos6 +……, теперь находим значения коэффициентов А, В.
А = 1 + 3/4е2 + 45/64е4 + 175/256е6 + …………..
В = 3/4е2 + 15/16е4 + 525/512е6 + ……….Подставляя эти значения коэффициентов в знаменатель формулы (1.11) и, принимая d = arc1 , получим следующее выражение длины одной минуты дуги меридиана:
S = a(1-e2) A arc1 - a(1-e2) B arc1 Cos2.
Подставляя значения параметров эллипсоида Красовского а и е2:
а(1-е2) А = 6 368 027,5
а(1-е2) В = 32 073 и значение d = arc1 =
получим окончательно:
S = 1852,25 – 9,31 Cos2 метры (1.12)
Как видим, длина одной минуты дуги меридиана величина переменная, зависит от удвоенной широты места исследуемой точки и меняется в пределах от 1843,0 м на экваторе и до 1861,6 м на полюсе.
В навигации принято Землю принимать за шар, у которого длина одной минуты дуги меридиана равна округленной до целого значения величины 1852 метра.
Эту величину морской мили в метрах узаконили на Международном гидрографическом бюро в Монако в 1928 году.
6. Понятие о геодезической линии, прямая геодезическая задача.
Геодези́ческая (Геодези́ческая ли́ния) — кривая определённого типа, обобщение понятия «прямая» в искривлённых пространствах. Конкретное определение геодезической линии зависит от типа пространства. Например, на двумерной поверхности, вложенной в евклидово трёхмерное пространство, геодези́ческие ли́нии — это линии, достаточно малые дуги которых являются на этой поверхности кратчайшими путями между их концами. На плоскости это будут прямые, на круговом цилиндре — винтовые линии, прямолинейные образующие и окружности, на сфере — дуги больших окружностей.
Прямая геодезическая задача
В геодезии часто приходится передавать координаты с одной точки на другую. Например, зная исходные координаты точки А (рис.23), горизонтальное расстояние SAB от неё до точки В и направление линии, соединяющей обе точки (дирекционный угол αAB или румб rAB), можно определить координаты точки В. В такой постановке передача координат называется прямой геодезической задачей.
Рис. Прямая геодезическая задача
Для точек, расположенных на сфероиде, решение данной задачи представляет значительные трудности. Для точек на плоскости она решается следующим образом.
Дано: Точка А( XA, YA ), SAB и αAB.
Найти: точку В( XB, YB ).
Непосредственно из рисунка имеем:
ΔX = XB – XA ;
ΔY = YB – YA .
Разности ΔX и ΔY координат точек последующей и предыдущей называются приращениями координат. Они представляют собой проекции отрезка АВ на соответствующие оси координат. Их значения находим из прямоугольного прямоугольника АВС:
ΔX = SAB · cos αAB ;
ΔY = SAB · sin αAB .
Так как в этих формулах SAB всегда число положительное, то знаки приращений координат ΔX и ΔY зависят от знаков cos αAB и sin αAB. Для различных значений углов знаки ΔX и ΔY представлены в табл.1.
Знаки приращений координат ΔX и ΔY Приращения координат Четверть окружности в которую направлена линия
I (СВ) II (ЮВ) III (ЮЗ) IV (СЗ)
ΔX + – – +
ΔY + + – – Таблица 1.
При помощи румба приращения координат вычисляют по формулам:
ΔX = SAB · cos rAB ;
ΔY = SAB · sin rAB .
Знаки приращениям дают в зависимости от названия румба.
Вычислив приращения координат, находим искомые координаты другой точки:
XB = XA + ΔX ;
YB = YA + ΔY .
Таким образом можно найти координаты любого числа точек по правилу: координаты последующей точки равны координатам предыдущей точки плюс соответствующие приращения.