27. Радиальная средняя квадратическая погрешность места судна.

Более простая по сравнению с эллипсом ошибок и по этой причине

более распространенная оценка точности места судна производится

посредством средней квадратической ошибки обсервованной

точки. Рассчитывается СКО точки как диагональ прямоугольника,

построенного на полуосях эллипса ошибок, или, что то же самое, как

радиус М окружности

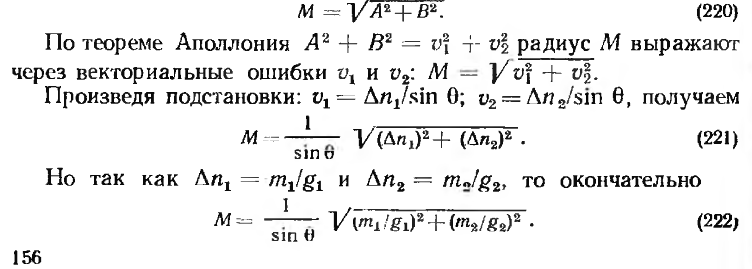
Из формулы (222) следует, что точность определения места судна

будет тем выше, чем меньше СКО т₁ и m₂ измерений навигационных

параметров и чем больше модули g₁ и g ₂ их градиентов.

Существенно зависит величина СКО М обсервованной точки от

угла 0 между линиями положения. Если модули градиентов —

величины постоянные, в частности равны единице, то ошибка М

будет наименьшей при 0 = 90°. В других случаях минимум ошибки

М наступает, когда угол 0 отличается — иногда весьма значительно

— от прямого в большую или меньшую сторону.

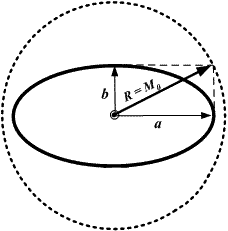
Среднюю квадратическую ошибку М называют радиальной.

Центр окружности радиуса М принимают в обсервованной точке.

В области, ограниченной этой окружностью, находится с определенно

вероятностью истинное место судна.

28. Вероятнейшее место судна в море.

Определяется эллипсом погрешностей

При ОМС составляется и решается уравнение, прокладывается изолиния или ЛП отягощенная ошибками измерений. Величины и знаки истинных ошибок измерений носят случайный характер, и учесть их можно лишь статистически.

Вывод формул оценки точности места базируется на предположениях:

5. Грубые ошибки или промахи, пропущенные при измерениях, исключены.

6. Компенсированы систематические ошибки измерений

7. Ошибки вычислений и графики малы и несущественны

8. Случайные ошибки измерения подчинены нормальному закону распространения случайных величин.

Д остоинства оценки места судна эллипсом.

5. Он имеет строго теоретическое обоснование.

6. Это единственная кривая, во всех точках которой плотность вероятности ошибки постоянна.

7. Вероятность попадания истинного места судна в область, ограниченную эллипсом, больше, чем у любой другой фигуры одинаковой с эллипсом площади.

8. Эллипс дает рассеяние мест судна по направлениям.

При двух ЛП на практике, достаточно вписать приближенный эллипс в четырёхугольник, образованный полосами погрешностей. При этом вероятнейшим местом судна будет точка пересечения ЛП - центр эллипса погрешностей из-за того, что в элементарно малых окрестностях этой точки вероятность нахождения места судна больше, чем в аналогичных окрестностях любой другой точки.

Для строгого построения эллипса погрешностей рассматриваются векториальные ошибки , линии положения 1 и 2 по направлению ЛП₂ и ЛП₁.

Учитывая, что вектора - сопряжённые полуоси эллипса используют теорему Аполлония

( 0 )

или

( 0 )

;

Где  угол, определяющий направление большой полуоси эллипса, который всегда откладывается внутри острого угла  от более точной ЛП.

Ещё один способ расчета эллипса погрешностей по 2-м ЛП, заключается в использовании таблицы прил. № 5 к МТ-75 Аргументами для входа в таблицу служат величины

и

( 0 )

угол. Из таблицы выбирают К_а, К_b и Полуоси рассчитывают по формуле:

Таблица приложений S составлена по преобразованным формулам Аполлония.

( 0 )

;

Рис. 18.10. Погрешность обсервованного места судна

Поскольку обсервованное место судна образуется пересечением минимум двух линий положения, а, значит, и двух полос, то на путевой карте мы получим не точку С (рис. 18.10), а так называемую фигуру погрешностей «абсд». Размеры этой фигуры при неизменных m_ЛП будут зависеть, прежде всего, от угла пересечения линий положения – угла θ.

При  θ = 90° площадь фигуры погрешностей наименьшая, а при m_ЛП1 = m_ЛП2 – квадрат. Но, чем меньше будет этот  θ, тем больше будет площадь фигуры погрешностей «абсд».

Вероятность нахождения обсервованного места судна в этой фигуре погрешностей равна произведению вероятностей нахождения места судна в каждой из полос, то есть: Р = 0,68 · 0,68 ≈ 0,46 (46%).

Однако, точность места судна принято оценивать не параллелограммом «абсд» (ромбом, квадратом) погрешностей, а эллипсом, вписанным в этот параллелограмм (рис. 18.11).

Рис. 18.11. Эллиптическая погрешность обсервованного места судна

8. Рассчитать градиенты g линий положения

9. Рассчитать смещение всех ЛП:

10. Определить абсолютные веса ЛП

11. Найти вероятнейшее место судна центрографическим способом или штурманским приемом. Вероятнейшее место судна – центр эллипса погрешностей.

12. Построить полигон весов.

В свободном месте карты в крупном масштабе строят векторную сумму абсолютных весов под двойными углами 2_i каждой ЛП к меридиану.

Величина результирующего вектора построения дает величину в масштабе построения, а его угол с его угол с N_u равен 2₀.

Арифметическая сумма даст величину

( 0 )

решив систему уравнения полуосей эллипса получим:

( 0 )

,

веса полуосей эллипса

13. Р

    ( 0 )

    ассчитать величины полуосей эллипса.

14. Под углом  к Nu c центром в вероятнейшем месте судна построить эллипс погрешностей, который двумя взаимноперпендикулярными ЛП в виде осей эллипса эквивалентен информации всех исходящих ЛП.

Вероятность нахождения места судна внутри эллипса 0,39, а для выполнения требований ИМО строят эллипс с полуосями, увеличенными в 2,5 раза.