Задача № 2.

Выполнить следующие расчеты.

1. Рассчитать показатели динамики с постоянной и переменной базой сравнения.

2. Графически изобразить показатели динамики с постоянной и переменной базой сравнения.

3. Рассчитать среднегодовые показатели ряда динамики.

4. Произвести сглаживание ряда методом трехлетней скользящей средней.

5. Выровнять ряд по прямой.

6. Построить график искомого и выровненного ряда.

7. Использовать полученное уравнение для экстраполяции уровней на следующий календарный год.

8. Сделать выводы.

Таблица 2.1 – Исходные данные

Годы Показатель	2002	2003	2004	2005	2006	2007	2008
1	2	3	4	5	6	7	8
Производство эл. энергии эл. станциями, млрд. кВт-ч	506,7	740,9	1038,6	1293,9	1544,2	1722	1722

Решение

1. Запишем формулы для расчета показателей динамики с постоянной и переменной базой сравнения.

Абсолютный прирост показывает, насколько в абсолютном выражении уровень отчетного периода больше или меньше уровня базисного периода и вычисляется по формулам

(переменная база сравнения);

(постоянная база сравнения);

– уровень ряда, принятого за базу сравнения.

Коэффициент роста показывает, во сколько раз уровень отчетного периода больше или меньше уровня базисного периода и вычисляется по формулам

или .

Коэффициенты роста, выраженные в процентах, носят название темпов роста .

Темп прироста показывает, насколько процентов уровень отчетного периода больше или меньше уровня базисного и вычисляется по формуле

или .

Абсолютное значение прироста вычисляется по формуле

или .

Используя вышеприведенные формулы, находим показатели динамики с постоянной и переменной базой сравнения и заносим их в таблицу 2.2 и таблицу 2.3 соответственно.

Таблица 2.2 – Показатели динамики с постоянной базой сравнения

, млрд. кВт-ч	, млрд. кВт-ч	, млрд. кВт-ч		, %	, %
740,9	506,7	234,2	1,462	146,2	46,2
1038,6	506,7	531,9	2,05	205	105
1293,9	506,7	787,2	2,554	255,4	155,4
1544,2	506,7	1037,5	3,048	304,8	204,8
1722	506,7	1215,3	3,398	339,8	239,8
1722	506,7	1215,3	3,398	339,8	239,8

Таблица 2.3 – Показатели динамики с переменной базой сравнения

, млрд. кВт-ч	, млрд. кВт-ч	, млрд. кВт-ч		, %	, %	, млрд. кВт-ч
740,9	506,7	234,2	1,462	146,2	46,2	5,1
1038,6	740,9	297,7	1,402	140,2	40,2	7,4
1293,9	1038,6	255,3	1,246	124,6	24,6	10,4
1544,2	1293,9	250,3	1,193	119,3	19,3	12,9
1722	1544,2	177,8	1,115	111,5	11,5	15,4
1722	1722	0	1	100	0	17,2

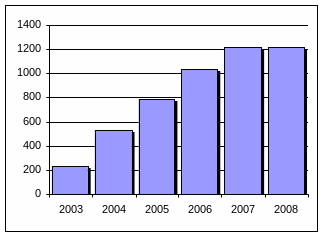
2. Графическое изображение (столбиковая диаграмма) показателей динамики с постоянной и переменной базой сравнения.

а) с постоянной базой сравнения	б) с переменной базой сравнения
Рисунок 2.1 – Динамика абсолютного прироста производства эл. энергии эл. станциями
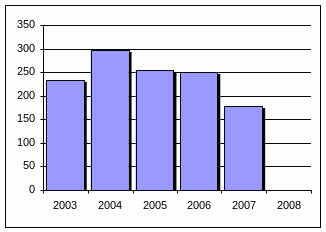
а) с постоянной базой сравнения	б) с переменной базой сравнения
Рисунок 2.2 – Динамика темпов роста производства эл. энергии эл. станциями
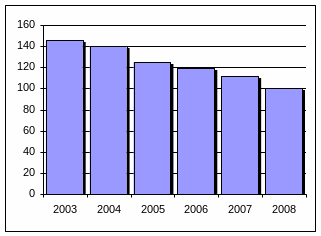
а) с постоянной базой сравнения	б) с переменной базой сравнения
Рисунок 2.3 – Динамика темпов прироста производства эл. энергии эл. станциями
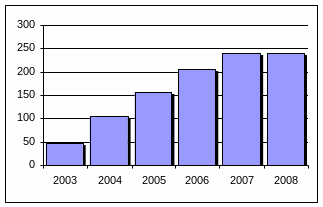
Рисунок 2.4 – Динамика абсолютного значения прироста производства эл. энергии эл. станциями

3. Рассчитаем среднегодовые показатели ряда динамики производства эл. энергии эл. станциями.

Среднегодовое производство эл. энергии эл. станциями вычислим по формуле средней арифметической простой.

Средняя арифметическая простая исчисляется путем деления суммы значений признака на число значений:

,

где – средняя арифметическая;

– отдельные значения признака;

– число значений признака.

Тогда среднегодовое производство эл. энергии составит

млрд. кВт-ч.

Средний абсолютный прирост вычислим по формуле

.

Получим

млрд. кВт-ч.

Средний коэффициент роста вычислим по формуле

,

следовательно, .

Так как средний темп роста , то .

Средний темп прироста определяется, исходя из темпа роста, т.е. . Следовательно, .

4. Выполним сглаживание ряда методом трехлетней скользящей средней.

Метод скользящей средней заключается в том, что вычисляется средний уровень из определенного числа первых по порядку уровней ряда, затем – средний уровень из такого же числа уровней, начиная со второго и т.д.:

; ; …

Все вычисления сведем в таблицу 2.4.

Таблица 2.4 – Сглаживание ряда методом трехлетней скользящей средней

Годы	Производство эл. энергии эл. станциями, млрд. кВт-ч	Расчет скользящих средних	Сглаженные уровни ряда
2002	506,7	–	–
2003	740,9		762,067
2004	1038,6		1024,467
2005	1293,9		1292,233
2006	1544,2		1520,033
2007	1722		1662,733
2008	1722	–	–

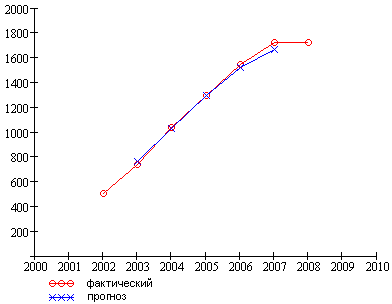
Рисунок 2.5 – Скользящее среднее по трем уровням

5. Выровняем ряд по прямой.

Выравнивание ряда по прямой предусматривает решение следующего уравнения: , где – время (порядковый номер интервала или момент времени).

Параметры находим решив систему:

Расчет параметров значительно упрощается, если :

– средний уровень ряда; – средний абсолютный прирост.

Составим расчетную таблицу 2.5.

Таблица 2.5 – Расчет параметров

Годы
2002	–3	506,7	-1520,1	9
2003	–2	740,9	-1481,8	4
2004	–1	1038,6	-1038,6	1
2005	0	1293,9	0	0
2006	1	1544,2	1544,2	1
2007	2	1722	3444	4
2008	3	1722	5166	9
	0	8568,3	6113,7	28

Пользуясь результатами, полученными в таблице, находим

, .

Таким образом, получено следующее уравнение: .

Проверяем правильность расчета уровней выровненного ряда динамики производства эл. энергии эл. станциями (сумма значений эмпирического ряда должна совпадать с суммой вычисленных значений выровненного ряда). Вычисления занесем в расчетную таблицу 2.6.

Таблица 2.6 – Значения эмпирического и выровненного рядов

Годы
2002	506,7	–3	569,005
2003	740,9	–2	787,351
2004	1038,6	–1	1005,697
2005	1293,9	0	1224,043
2006	1544,2	1	1442,389
2007	1722	2	1660,735
2008	1722	3	1879,081
	8568,3	0	8568,3

Из последней строки таблицы 2.6 видно, что уравнение составлено правильно.

6. Построим график искомого и выровненного ряда.

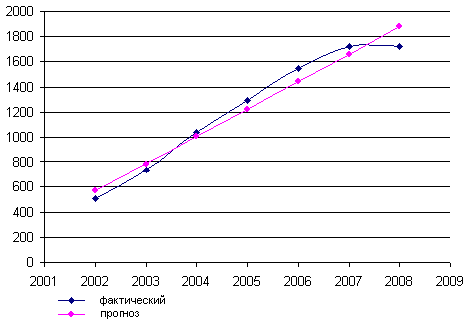
Рисунок 2.6 – Динамика производства эл. энергии эл. станциями (выровненный ряд по прямой)

7. Выполним экстраполяцию уровней на следующий календарный год.

В пункте 5 было получено следующее уравнение: .

Для прогнозирования данных на 2009 год, следуя логике, параметр . Следовательно, производства эл. энергии эл. станциями в 2009 году будет равно млрд. кВт-ч.

ВЫВОДЫ

Таблица 2.7 – Итоговая таблица

Годы	Производство эл. энергии эл. станциями, млрд. кВт-ч	Абсолютный прирост , млрд. кВт-ч		Темп роста , %		Темп прироста , %		Абсолютное значение 1 % прироста , млрд. кВт-ч
		базисный	цепной	базисный	цепной	базисный	цепной
2002	506,7	–	–	–	–	–	–	–
2003	740,9	234,2	234,2	146,2	146,2	46,2	46,2	5,1
2004	1038,6	531,9	297,7	205	140,2	105	40,2	7,4
2005	1293,9	787,2	255,3	255,4	124,6	155,4	24,6	10,4
2006	1544,2	1037,5	250,3	304,8	119,3	204,8	19,3	12,9
2007	1722	1215,3	177,8	339,8	111,5	239,8	11,5	15,4
2008	1722	1215,3	0	339,8	100	239,8	0	17,2

Как показывают полученные результаты, производство эл. энергии эл. станциями постоянно увеличивалось. В целом за исследуемый период производство эл. энергии увеличилось на 1215,3 млрд. кВт-ч (3 столбец) или 239,8% (7 столбец). Увеличение производства эл. энергии подтверждается систематическим ростом величины абсолютного значения 1% прироста: с 5,1 до 17,2 млрд. кВт-ч.

Среднегодовое производство эл. энергии эл. станциями составляет 1224,043 млрд. кВт-ч.

За исследуемый период выявлена положительная динамика производства эл. энергии: ежегодный рост производства эл. энергии составляет 202,55 млрд. кВт-ч или 22,6%.

В соответствии с графиком (рис. 2.5), построенным по результатам сглаживания ряда методом скользящей средней, прослеживается равномерная и положительная тенденция увеличения производства эл. энергии.

На рис. 2.5 и рис. 2.6 фактические данные представляет ломанная линия, свидетельствующая о подъемах объема производства эл. энергии. Вторая линия (рис. 2.5) на графике показывает, что применение метода скользящей средней (линия со срезанными концами) позволяет существенно выровнять уровни динамического ряда и соответственно на графике ломаную кривую линию сделать более плавной, сглаженной. Однако выравненные линии все же остаются кривыми линиями. Построенная на базе теоретических значений ряда, полученных по математическим формулам, линия (рис. 2.6) строго соответствует прямой линии.

Прогноз на 2009 год показал, что производство эл. энергии в этом году составит 2097,427 млрд. кВт-ч.