1. Статистика. Основные понятия. Статистическое наблюдение.

Статистика - отрасль знаний, в которой излагаются общие вопросы сбора, измерения и анализа массовых статистических данных; изучение количественной стороны массовых общественных явлений в числовой форме.

Статистические совокупности - изучаемые статистикой массовые явления в виде множества однокачественных единиц с отличающимися индивидуальными признаками.

Единицы совокупности - элементы, множество которых образует изучаемую совокупность.

Вариация – различные значения определенного признака у различных единиц совокупности.

Статистическая закономерность - Закономерность, выявленная на основе массового наблюдения, т.е. проявившаяся в большой массе явлений через преодоление свойственной ее единичным элементом случайности.

Основная задача статистики – это абстрагироваться от случайного и выявить типичное, закономерное. Способы выявления закономерности – логический, эмпирический, на основе закона больших чисел.

Статистическое наблюдение - это предварительная стадия статистического исследования, которая представляет собой планомерный, научно организованный учет первичных статистических данных о массовых социально-экономических явлениях и процессах.

Наблюдение будет статистическим, во-первых, когда оно сопровождается регистрацией изучаемых фактов в соответствующих учетных документах для дальнейшего их обобщения, во-вторых - когда носит массовый характер.

2. Статистическое наблюдение. Группировки.

Статистическое наблюдение - сбор первичного статистического материала

Основные этапы:

• подготовка статистического наблюдения (определяется цель, устанавливаются объект и единица наблюдения, разрабатываются инструментарий и программа наблюдения)

• организация и производство наблюдения ( выбрать соответствующие целям и задачам конкретного статистического наблюдения организационные формы наблюдения, виды наблюдения и способы получения статистической информации.)

• контроль полученных первичных данных (собранный статистический материал должен пройти контроль)

Цель определяет объект статистического наблюдения.

Объект наблюдения - исследуемая статистическая совокупность или физических лиц, или юридических лиц , или физических единиц , т.е. исследуемая статистическая совокупность состоит из отдельных единиц.

Единица наблюдения - это первичный элемент объекта статистического наблюдения, который является носителем признаков, подлежащих регистрации.

Единицу наблюдения следует отличать от отчетной единицы. Отчетной называют такую единицу, от которой поступают отчетные данные. Она может совпадать или не совпадать с единицей наблюдения.

По форме организации статистического наблюдения: отчетность; специально организованное статистическое обследование - перепись; регистры.

По видам статистического наблюдения:

а) по времени регистрации фактов (текущее или непрерывное; прерывное - периодическое, единовременное);

б) по охвату единиц совокупности (сплошное; не сплошное - основного массива, выборочное, монографическое).

По способам получения статистической информации: непосредственное наблюдение; документальный способ; опрос - экспедиционный, анкетный, явочный, корреспондентский, саморегистрация.

Основной формой статистического наблюдения является отчетность. Если первичный учет (первичный учетный документ) регистрирует различные факты, то отчетность является обобщением первичного учета.

Группировки -метод обработки и анализа статистических данных, при котором изучаемая совокупность явлений расчленяется на однородные по отдельным признакам группы и подгруппы и каждая из них характеризуется системой статистических показателей.

Кроме анализа структуры совокупности, метод группировок применяется при характеристике типов явлений и изучении взаимосвязей между различными признаками или факторами.

3. Вариация признаков. Ряды распределения и их графическое изображение.

Вариация - колеблемость, изменяемость величины признака у единиц совокупности. Отдельные числовые значения признака, встречающиеся в изу­чаемой совокупности, называют вариантами значений.

Статистические ряды распределения представляют собой упорядоченное распределение единиц изучаемой совокупности на группы по группировочному признаку.

Делятся на:

• Атрибутивные ряды образуются по качественным признакам, которыми могут выступать занимаемая должность работников торговли, профессия, пол, образование и т.д.

• Вариационные ряды строятся на основе количественного группировочного признака. Вариационные ряды состоят из двух элементов: вариант и частот. Вариационные ряды в зависимости от характера вариации подразделяются на дискретные (прерывные) и интервальные (непрерывные). Дискретные ряды распределения основаны на дискретных (прерывных) признаках, имеющих только целые значения (например, тарифный разряд рабочих, число детей в семье). Интервальные ряды распределения базируются на непрерывно изменяющемся значении признака, принимающем любые (в том числе и дробные) количественные выражения, т.е. значение признаков таких рядах задается в виде интервала.

Варианта - это отдельное значение варьируемого признака, которое он принимает в ряду распределения. Они могут быть положительными и отрицательными, абсолютными и относительными. Частота - это численность отдельных вариант или каждой группы вариационного ряда. Частоты, выраженные в долях единицы или в процентах к итогу, называются частостями. Сумма частот называется объемом совокупности и определяет число элементов всей совокупности.

Частости - это частоты, выраженные в виде относительных величин (долях единиц или процентах). Сумма частостей равна единице или 100 %. Замена частот частостями позволяет сопоставлять вариационные ряды с разным числом наблюдений.

При наличии достаточно большого количества вариантов значений признака первичный ряд является труднообозримым, и непосредственное рассмотрение его не дает представления о распределении единиц по значению признака в совокупности. Поэтому первым шагом в упорядочении первичного ряда является его ранжирование - расположение всех вариантов в возрастающем (убывающем) порядке.

Для построения дискретного ряда с небольшим числом вариантов выписываются все встречающиеся варианты значений признака , а затем подсчитывается частота повторения варианта . Ряд распределения принято оформлять в виде таблицы, состоящей из двух колонок (или строк), в одной из которых представлены варианты, а в другой - частоты.

Для построения ряда распределения непрерывно изменяющихся признаков, либо дискретных, представленных в виде интервалов, необходимо установить оптимальное число групп (интервалов), на которые следует разбить все единицы изучаемой совокупности.

Полигон – графическое изображение дискретного вариационного ряда распределения, дающее представление о характере изменения его частот. Для построения полигона по оси абсцисс в одинаковом масштабе откладываются ранжированные значения варьирующего признака, по оси ординат – частоты или частости.

Гистограмма (ленточная диаграмма) – графическое изображение интервального вариационного ряда распределения, дающее представление о характере изменения его частот. При построении гистограммы по оси абсцисс откладываются величины интервалов соответствующего признака, по оси ординат – частоты, частости или плотности распределения.

Кумулята – графическое изображение кумулятивной кривой, дающее представление о характере изменения накопленных частот/частостей. Для построения кумуляты интервального вариационного ряда по оси абсцисс откладываются величины интервалов, а если ряд дискретный - ранжированные значения признака. По оси ординат в обоих случаях располагаются накопленные частоты или частости. Равенство или неравенство интервалов для графика кумуляты значения не имеет.

4. Мода и медиана. Методы расчёта. Свойства.

Средняя квадратическая служит для измерение вариации признака.

• Мода - это величина признака (варианта), который наиболее часто встречается в данной совокупности, т.e. это варианта, имеющая наибольшую частоту.

• Медиана – значение, лежащее в середине ранжированного ряда, делит ряд на две равные части.

Квантиль распределения – это значение признака, занимающее определенное место в упорядоченной по данному признаку совокупности.

Виды квантилей:

медиана (Ме) - значение признака, приходящееся на середину упорядоченной совокупности,

Например, по данным о 12 предприятий розничной торговли требуется определить медиану и квартили для признака х – объем продаж за период, тыс. усл. ден. ед.

Упорядочим совокупность по х (табл. 3.4). В совокупности 12 единиц. Середина приходится на 6 и 7 элементы, значения признака у которых 31 и 32 соответственно. Медианой будет среднее из значений этих элементов:

Значение медианы можно определить графически по кумуляте. Для этого максимальную ординату кумуляты делят пополам. И через полученное значение проводят линию параллельную горизонтальной оси. Абсцисса точки пересечения этой линии и кумуляты дает значение медианы, совпадет со значением, полученным при расчете по сгрупированным данным. Наиболее распространенным видом квантилей является медиана. Медиана не требует знания всех индивидуальных значений признака. Она не чувствительна к крайним значениям признака, которые могут резко отличаться от основной массы его значений. Поэтому медиану используют как наиболее надежный показатель типичного значения признака в неоднородной совокупности (включающей резкие отклонения от ). Медиана находит практическое применение также вследствие особого математического свойства - свойства минимальности. Согласно данному свойству сумма абсолютных отклонений чисел ряда от медианы есть величина наименьшая:

• .

Мода (Мо) – наиболее часто встречающееся значение признака в совокупности. Для дискретного ряда мода – это значение признака, которому соответствует наибольшая частота (частость) распределения. Для интервального ряда – это значение признака, которому соответствует наибольшая плотность распределения. Если ряд равноинтервальный, то значение моды можно определить по частотам (частостям): их соотношение будет таким же, что и плотностей распределения. Кроме того, значение моды в случае равноинтервального ряда можно уточнить по формуле:

• 

где X_Mo - нижняя граница интервала, в котором находится мода;

- величина модального интервала;

N_Mо, N_Mо-1, N_Mо+1 – частоты, соответственно, модального, предшествующего и последующего интервалов.

5. Средняя арифметическая и её свойства, методы расчёта.

Средняя арифметическая. Гармоническая, геометрическая и квадратическая средние

Показатель степени k в формуле степенной средней определяет вид степенной средней. При k = -1 имеем гармоническую среднюю; при k = 0 - среднюю геометрическую; k = 1 - среднюю арифметическую; k =2 - среднюю квадратическую.

Виды степенных средних

K	Название средней	Формула расчета средней		Область применения
		Простая	Взвешенная
1	2	3	4	5
-1	Гармоническая			Усреднение относительных величин (за исключением относительных показателей динамики)
1	Арифметическая			Усреднение абсолютных, относительных величин (за исключением относительных показателей динамики)
2	Квадратическая			Например, для вычисления средней величины стороны n квадратных участков, средних диаметров n труб, стволов и т.п., при построении показателя вариации

Свойства средней арифметической

Наиболее распространенным видом степенной средней является средняя арифметическая. Она обладает рядом свойств.

Сущностные свойства:

1. Средняя арифметическая постоянной величины равна этой постоянной.

2. Алгебраическая сумма линейных отклонений (разностей) индивидуальных значений признака от средней арифметической равно нулю: .

3. Сумма квадратов отклонений индивидуальных значений признака от средней арифметической есть величина минимальная:

или

где А - константа.

6. Показатели вариации, их свойства, методы расчёта, применение.

Вариационный анализ. Показатели вариации и их значение в статистике

Средняя величина дает обобщающую характеристику всей совокупности изучаемого явления. Однако два распределения, имеющие одинаковую среднюю арифметическую, могут значительно отличаться друг от друга по степени рассеяния (вариации) признака. Если индивидуальные значения признака ряда мало отличаются друг от друга (рис. 3.1 А), то средняя арифметическая будет достаточно надежной показательной характеристикой типичного уровня в данной совокупности. Если же ряд распределения характеризуется значительным рассеиванием индивидуальных значений признака (рис. 3.2 Б), то средняя арифметическая будет ненадежной характеристикой типичного уровня этой совокупности и ее практическое применение будет ограничено.

А ) ··········· Х

Б ) · · · · · ·  · · · · · Х

Рис. 3.1. Распределения с малой (А) и большой (Б)

вариацией.

Вариационный размах, дисперсия, коэффициент вариации. Свойства и методы расчета показателей вариации

Для измерения рассеяния (вариации) признака применяются различные абсолютные и относительные показатели вариации.

К абсолютным показателям вариации относятся:

• Размах вариации, R - разность между максимальным и минимальным значениями признака в совокупности:

Среднее по совокупности отклонение индивидуального значения признака от его среднего уровня измеряют два следующих показателя вариации: среднее линейное и среднее квадратическое отклонение.

• Среднее линейное отклонение, d - представляет собой среднюю арифметическую абсолютных значений отклонений отдельных вариант от их средней арифметической (при этом всегда полагают, что среднюю вычитают из варианты). Для несгруппированных и сгруппированных данных, соответственно:

, ,

где N – объем совокупности;

k - число групп;

f_j – частота/частость в j – ой группе.

Математические свойства модулей плохие, поэтому часто на практике применяют другой показатель среднего отклонения от средней - среднеее квадратическое отклонение.

• Среднее квадратическое отклонение,  - представляет собой среднюю квадратическую из отклонений отдельных вариант от их средней арифметической. Для несгруппированных и сгруппированных данных, соответственно:

, .

• Дисперсия, ² - это квадрат среднего квадратического отклонения. Она представляет собой средний квадрат отклонений вариант от их средней величины. Она может быть также вычислена, как разность среднего квадрата значения признака и квадрата среднего арифметического значения признака:

.

Среднее квадратическое отклонение наряду с дисперсией входят в большинство теорем теории вероятности и математической статистики, что обусловливает их широкое применение на практике. Кроме того, дисперсия может быть разложена на составные части, позволяющие оценить влияние различных факторов, обусловливающих вариацию признака.

Теорема (правило) о разложении дисперсии при группировании. Пусть при группировке совокупности по некоторому признаку Х было образовано k однородных групп. Согласно теореме общая дисперсия признака Х (по совокупности в целом) может быть разложена на две составные части: 1) межгрупповую и 2) остаточную (среднюю из внутригрупповых) дисперсии:

Общая дисперсия рассчитывается по формуле простой дисперсии и показывает величину вариации признака, обусловленную всеми факторами, влияющими на данный признак.

Межгрупповая дисперсия, - характеризует ту часть общей вариации признака, которая обусловлена делением совокупности на группы. Если деление совокупности на группы обусловлено факторами, влияющими на интересующий нас признак, то данную дисперсию называют еще факторной дисперсией. Межгрупповая дисперсия равна среднему взвешенному квадрату отклонений групповых (частных) средних от общей средней :

,

где Nj- численность единиц в j - ой группе.

Средняя из внутригрупповых (или остаточная) дисперсия, - характеризует остаточную вариацию, несвязанную с группированием. То есть, характеризует вариацию признака, обусловленную прочими факторами, не связанными с делением совокупности на группы. Вычисляется она как средняя взвешенная из внутригрупповых дисперсий:

,

где _j² - дисперсия признака внутри j–ой группы.

Основные вычислительные свойства дисперсии:

1. дисперсия постоянной величины равна 0;

2. если все варианты значений признака уменьшить на одно и то же число, то дисперсия не изменится;

3. если все варианты значений признака уменьшить в одно и то же число А раз (А-const), то дисперсия уменьшится в А² раз.

Относительные показатели вариации применяют, если необходимо оценить интенсивность вариации, или сравнить вариацию признака в различных совокупностях, или сравнить вариацию различных признаков. Показатель относительной вариации рассчитывается как отношение абсолютного показателя вариации к среднему значению.

Самым распространенным относительным показателем рассеяния является коэффициент вариации. Он представляет собой выраженное в процентах отношение среднего квадратического отклонения к средней арифметической:

.

Коэффициент вариации используют также как характеристику однородности совокупности. Совокупность считается количественно однородной, если коэффициент вариации не превышает 33%.

Показатели формы распределения: показатели асимметрии и характеристики эксцесса распределения

Для характеристики однородности совокупности помимо показателей вариации можно использовать показатели формы распределения: коэффициент асимметрии и эксцесс.

Коэффициент асимметрии, As - показатель симметричности распределения. Симметричным является распределение, в котором частоты любых двух вариант, равноотстоящих в обе стороны от центра распределения, равны между собой. Для симметричных одновершинных распределений средняя арифметическая, мода и медиана равны между собой. Положительная величина показателя асимметрии указывает на наличие правосторонней асимметрии, отрицательная – на наличие левосторонней асимметрии (рис. 3.2.). Близость нулю показателя асимметрии свидетельствует о симметричном распределении.

As<0 As>0

а) б)

Рис. 3.2. Виды асимметрии: а) левосторонняя; б) правосторонняя

Существуют различные способы расчета коэффициента асимметрии:

1. Коэффициент асимметрии Пирсона:

.

Величина As может изменяться от –1 до +1 (для одновершинных распределений). Чем ближе по модулю As к 1, тем асимметрия существеннее.

2. Наиболее точным и распространенным является показатель, основанный на определении центрального момента третьего порядка – М3:

.

В симметричном распределении его величина равна нулю. Для оценки существенности такого коэффициента асимметрии вычисляется показатель средней квадратической ошибки коэффициента асимметрии:

,

где N - объем совокупности.

Отношение As/_As, дающее значение меньше 2, свидетельствует о несущественном характере асимметрии.

Коэффициент эксцесса, Ex - показатель островершинности распределения. Он рассчитывается для симметричных распределений. Эксцесс представляет собой выпад вершины эмпирического распределения вверх или вниз от вершины кривой нормального распределения. Наиболее точным является показатель, использующий центральный момент четвертого порядка - М4:

.

Д ля нормального распределения отношение М4/⁴=3, следовательно эксцесс равен нулю. Наличие положительного эксцесса означает, что распределение более островершинное чем нормальное; отрицательное значение эксцесса означает более плосковершинный характер распределения, чем у нормального (рис. 3.3.).

Ex>0

Ex=0

Ex<0

Рис. 3.3. Эксцесс распределения.

Для оценки существенности коэффициента эксцесса вычисляется показатель средней квадратической ошибки коэффициента эксцесса:

,

где N - объем совокупности.

Отношение Ex/_Ex, дающее значение меньше 2, свидетельствует о несущественном характере эксцесса (близости распределения по характеру островершинности к нормальному).

7. Понятие выборочного наблюдения. Способы отбора. Оценки параметров наблюдения.

Выборочное наблюдение – наблюдение над частью совокупности, отобранной в случайном порядке. При правильной организации оно дает достаточно достоверные результаты, вполне пригодные для характеристики всей изучаемой совокупности. Выборочное наблюдение широко применяется в различных отраслях народного хозяйства. В промышленности - для контроля качества продукции, в сельском хозяйстве – при выявлении продуктивности скота, в торговле – при изучении степени удовлетворения спроса населения и т.д.

При выборочном методе изучению подвергается только некоторая часть изучаемой совокупности, при этом подлежащая изучению статистическая совокупность называется генеральной совокупностью.

Выборочной совокупностью или просто выборкой можно называть отобранную из генеральной совокупности часть единиц, которая будет подвергаться статистическому исследованию.

Значение выборочного метода: при минимальной численности исследуемых единиц проведение статистического исследования будет происходить в более короткие промежутки времени и с наименьшими затратами средств и труда.

Различают четыре вида отбора совокупности единиц наблюдения:

1) случайный;

2) механический;

3) типический;

4) серийный (гнездовой).

Случайный отбор – наиболее распространенный способ отбора в случайной выборке, его еще называют методом жеребьевки, при нем на каждую единицу статистической совокупности заготовляется билет с порядковым номером.

Механический отбор – это способ, когда вся совокупность разбивается на однородные по объему группы по случайному признаку, потом из каждой группы берется только одна единица Все единицы изучаемой статистической совокупности предварительно располагаются в определенном порядке, но в зависимости от объема выборки механически через определенный интервал отбирается необходимое количество единиц.

Типический отбор – это способ, при котором исследуемая статистическая совокупность разбивается по существенному, типическому признаку на качественно однородные, однотипные группы, затем из каждой этой группы случайным способом отбирается определенное количество единиц, пропорциональное удельному весу группы во всей совокупности.

Серийный (гнездовой) отбор. Отбору подлежат целые группы (серии, гнезда), отобранные случайным или механическим способом. По каждой такой группе, серии проводится сплошное наблюдение, а результаты переносятся на всю совокупность.

Повторный отбор. Каждая отобранная единица или серия возвращается во всю совокупность и может вновь попасть в выборку Это так называемая схема возвращенного шара.

Бесповторный отбор. Каждая обследованная единица изымается и не возвращается в совокупность, поэтому она не попадает в повторное обследование. Эта схема получила название невозвращенного шара.

Бесповторный отбор дает более точные результаты, потому что при одном и том же объеме выборки наблюдение охватывает большее количество единиц изучаемой совокупности.

Комбинированный отбор может проходить одну или несколько ступеней. Выборка называется одноступенчатой, если отобранные однажды единицы совокупности подвергаются изучению.

Выборка называется многоступенчатой, если отбор совокупности проходит по ступеням, последовательным стадиям, причем каждая ступень, стадия отбора имеет свою единицу отбора.

Многофазная выборка – на всех ступенях выборки сохраняется одна и та же единица отбора, но проводится несколько стадий, фаз выборочных обследований, которые различаются между собой широтой программы обследования и объемом выборки.

Характеристики параметров генеральной и выборочной совокупностей обозначаются следующими символами:

N – объем генеральной совокупности;

n – объем выборки;

X – генеральная средняя;

х – выборочная средняя;

р – генеральная доля;

w – выборочная доля;

?² – генеральная дисперсия (дисперсия признака в генеральной совокупности);

?² – выборочная дисперсия того же признака;

?– среднее квадратическое отклонение в генеральной совокупности;

?– среднее квадратическое отклонение в выборке.

8. Ошибка выборки. Определение точности оценки среднего и доли.

Собственнослучайная выборка – это отбор единиц из всей генеральной совокупности посредством жеребьевки или другим подобным способом.

Доля выборки – это отношение числа единиц выборочной совокупности к числу единиц генеральной совокупности:

Собственнослучайный отбор в чистом виде является исходным среди всех других видов отбора, в нем заключаются и реализуются основные принципы выборочного статистического наблюдения.

Два основных вида обобщающих показателей, которые используют в выборочном методе – это средняя величина количественного признака и относительная величина альтернативного признака.

Для характеристики надежности выборочных показателей различают среднюю и предельную ошибки выборки.

Ошибка выборки, ее еще называют ошибкой репрезентативности, представляет собой разность соответствующих выборочных и генеральных характеристик:

1) для средней количественного признака:

?х =|х – х|;

2) для доли (альтернативного признака):

?w =|х – p|.

Только выборочным наблюдениям присуща ошибка выборки

Выборочная средняя и выборочная доля – это случайные величины, принимающие различные значения в зависимости от единиц изучаемой статистической совокупности, которые попали в выборку. Соответственно ошибки выборки – тоже случайные величины и также могут принимать различные значения. Поэтому определяют среднюю из возможных ошибок – среднюю ошибку выборки.

Средняя ошибка выборки определяется объемом выборки: чем больше численность при прочих равных условиях, тем меньше величина средней ошибки выборки. Охватывая выборочным обследованием все большее количество единиц генеральной совокупности, все более точно характеризуем всю генеральную совокупность.

Средняя ошибка выборки зависит от степени варьирования изучаемого признака, в свою очередь степень варьирования характеризуется дисперсией ?² или w(l – w) – для альтернативного признака. Чем меньше вариация признака и дисперсия, тем меньше средняя ошибка выборки, и наоборот.

При случайном повторном отборе средние ошибки теоретически рассчитывают по следующим формулам:

1) для средней количественного признака:

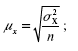
где ?² – средняя величина дисперсии количественного признака.

2) для доли (альтернативного признака):

Так как дисперсия признака в генеральной совокупности ?² точно неизвестна, на практике пользуются значением дисперсии S² , рассчитанным для выборочной совокупности на основании закона больших чисел, согласно которому выборочная совокупность при достаточно большом объеме выборки достаточно точно воспроизводит характеристики генеральной совокупности.

Формулы средней ошибки выборки при случайном повторном отборе следующие. Для средней величины количественного признака: генеральная дисперсия выражается через выборную следующим соотношением:

где S² – значение дисперсии.

Механическая выборка – это отбор единиц в выборочную совокупность из генеральной, которая разбита по нейтральному признаку на равные группы; производится так, что из каждой такой группы в выборку отбирается лишь одна единица.

При механическом отборе единицы изучаемой статистической совокупности предварительно располагают в определенном порядке, после чего отбирают заданное число единиц механически через определенный интервал. При этом размер интервала в генеральной совокупности равен обратному значению доли выборки.

Типическая выборка дает более точные результаты. Типизация генеральной совокупности обеспечивает репрезентативность такой выборки, представительство в ней каждой типологической группы, что позволяет исключить влияние межгрупповой дисперсии на среднюю ошибку выборки. Поэтому при определении средней ошибки типической выборки в качестве показателя вариации выступает средняя из внутригрупповых дисперсий.

Серийная выборка предполагает случайный отбор из генеральной совокупности равновеликих групп для того, чтобы в таких группах подвергать наблюдению все без исключения единицы.

9. Статистический анализ зависимостей. Статистические и функциональные зависимости. Эмпирически-регрессионный метод.

Возникновение понятия статистической связи обусловливается тем, что зависимая переменная подвержена влиянию ряда неконтролируемых или неучтенных факторов, а также тем, что измерение значений переменных неизбежно сопровождается некоторыми случайными ошибками

Статистическая зависимость между двумя переменными, при которой каждому значению одной переменной соответствует определенное среднее значение, т.е. условное математическое ожидание другой, называется корреляционной. Иначе, корреляционной зависимостью между двумя переменными величинами называется функциональная зависимость между значениями одной из них и условным ‑­ математическим ожиданием другой.

Корреляционная зависимость может быть представлена в виде:

Mx(Y)=φ(x) (1.1)

My(X)=ψ(x) (1.2)

Таким образом, из рассмотренных зависимостей наиболее общей выступает статистическая зависимость. Каждая корреляционная зависимость является статистической, но не каждая статистическая зависимость является корреляционной. Функциональная зависимость представляет частный случай корреляционной.

Уравнения (1.1) и (1.2) называются модельными уравнениями регрессии (или просто уравнениями регрессии) соответственно Y по Х и Х по Y, функции ψ(x) и φ(у) – модельными функциями регрессии (или функциями регрессии), а их графики - модельными линиями регрессии (или линиями регрессии).

Для отыскания модельных уравнений регрессии, вообще говоря, необходимо знать закон распределения двумерной случайной величины (Х,Y). На практике исследователь, как правило, располагает лишь выборкой пар значений (xi,yi) ограниченного объема. В этом случае речь может идти об оценке (приближенном выражении) по выборке функции регрессии. Такой наилучшей (в смысле метода наименьших квадратов) оценкой является выборочная линия (кривая) регрессии Y по Х

yx=φ(x,b0,b1,…,bp) (1.3)

Статистические связи между переменными можно изучать методами корреляционного и регрессионного анализа. Основной задачей регрессионного анализа является установление формы и изучение зависимости между переменными. Основной задачей корреляционного анализа – выявление связи между случайными переменными и оценка ее тесноты.

10. Эмпирически-регрессионный метод. Показатели тесноты связи.

Понятие степени тесноты связи между двумя признаками возникает вследствие того, что в реальной действительности на изменение результативного признака влияют несколько факторов. При этом влияние одного из факторов может выражаться более заметно и четко, чем влияние других факторов. С изменением условий в качестве главного, решающего фактора может выступать другой.

При статистическом изучении взаимосвязей, как правило, учитываются только основные факторы. А вопрос необходимо ли вообще изучать более подробно данную связь и практически ее использовать, решается с учетом степени тесноты связи.

Для характеристики степени тесноты корреляционной связи могут применяться различные статистические показатели: коэффициент Фехнера (КФ), коэффициент линейной (парной) корреляции, коэффициент детерминации, корреляционное отношение, индекс корреляции, коэффициент множественной корреляции, коэффициент частной корреляции и др.

Корреляционно-регрессионный метод анализа

Наиболее простым вариантом корреляционной зависимости является парная корреляция, т.е. зависимость между двумя признаками (результативным и факторным или между двумя факторными). Математически эту зависимость можно выразить как зависимость результативного показателя у от факторного показателя х. Связи могут быть прямые и обратные. В первом случае с увеличением признака х увеличивается и признак у, при обратной связи с увеличением признака х уменьшается признак у.

Непараметрические показатели связи

В статистической практике могут встречаться такие случаи, когда качества факторных и результативных признаков не могут быть выражены численно. Поэтому для измерения тесноты зависимости необходимо использовать другие показатели. Для этих целей используются так называемые непараметрические методы.

Наибольшее распространение имеют ранговые коэффициенты корреляции, в основу которых положен принцип нумерации значений статистического ряда. При использовании коэффициентов корреляции рангов коррелируются не сами значения показателей х и у, а только номера их мест, которые они занимают в каждом ряду значений. В этом случае номер каждой отдельной единицы будет ее рангом.

Коэффициенты корреляции, основанные на использовании ранжированного метода, были предложены К. Спирмэном и М. Кендэлом.

11. Аналитически-регрессионный метод. Показатели тесноты связи.

Корреляционно-регрессионный анализ — классический метод стохастического моделирования хозяйственной деятельности. Он изучает взаимосвязи показателей хозяйственной деятельности, когда зависимость между ними не является строго функциональной и искажена влиянием посторонних, случайных факторов. При проведении корреляционно-регрессионного анализа строят различные корреляционные и регрессионные модели хозяйственной деятельности. В этих моделях выделяют факторные и результативные показатели (признаки). В зависимости от количества исследуемых показателей различают парные и многофакторные модели корреляционно-регрессионного анализа.

Основной задачей корреляционно-регрессионного анализа является выяснение формы и тесноты связи между результативным и факторным показателями. Под формой связи понимают тип аналитической формулы, выражающей зависимость результативного показателя от изменений факторного. Различают связь прямую, когда с ростом (снижением) значений факторного показателя наблюдается тенденция к росту (снижению) значений результативного показателя. В противном случав между показателями существует обратная связь. Форма связи может быть прямолинейной (ей соответствует уравнение прямой линии), когда наблюдается тенденция равномерного возрастания или убывания результативного показателя, в противном случае форма связи называется криволинейной (ей соответствует уравнение параболы, гиперболы и др.).

ОСНОВНЫЕ МОДЕЛИ КОРРЕЛЯЦИОННОГО АНАЛИЗА. Такими моделями являются: коэффициент парной корреляции, коэффициент частной корреляции, коэффициент множественной корреляции, коэффициент детерминации.

Понятие степени тесноты связи между двумя признаками возникает вследствие того, что в реальной действительности на изменение результативного признака влияют несколько факторов. При этом влияние одного из факторов может выражаться более заметно и четко, чем влияние других факторов. С изменением условий в качестве главного, решающего фактора может выступать другой.

При статистическом изучении взаимосвязей, как правило, учитываются только основные факторы. А вопрос необходимо ли вообще изучать более подробно данную связь и практически ее использовать, решается с учетом степени тесноты связи.

Для характеристики степени тесноты корреляционной связи могут применяться различные статистические показатели: коэффициент Фехнера (КФ), коэффициент линейной (парной) корреляции, коэффициент детерминации, корреляционное отношение, индекс корреляции, коэффициент множественной корреляции, коэффициент частной корреляции и др.

Корреляционно-регрессионный метод анализа

Наиболее простым вариантом корреляционной зависимости является парная корреляция, т.е. зависимость между двумя признаками (результативным и факторным или между двумя факторными). Математически эту зависимость можно выразить как зависимость результативного показателя у от факторного показателя х. Связи могут быть прямые и обратные. В первом случае с увеличением признака х увеличивается и признак у, при обратной связи с увеличением признака х уменьшается признак у.

Непараметрические показатели связи

В статистической практике могут встречаться такие случаи, когда качества факторных и результативных признаков не могут быть выражены численно. Поэтому для измерения тесноты зависимости необходимо использовать другие показатели. Для этих целей используются так называемые непараметрические методы.

Наибольшее распространение имеют ранговые коэффициенты корреляции, в основу которых положен принцип нумерации значений статистического ряда. При использовании коэффициентов корреляции рангов коррелируются не сами значения показателей х и у, а только номера их мест, которые они занимают в каждом ряду значений. В этом случае номер каждой отдельной единицы будет ее рангом.

Коэффициенты корреляции, основанные на использовании ранжированного метода, были предложены К. Спирмэном и М. Кендэлом.

12. Линейная регрессия.

Линейная регрессия — используемая в статистике регрессионная модель зависимости одной (объясняемой, зависимой) переменной y от другой или нескольких других переменных (факторов, регрессоров, независимых переменных) x с линейной функцией зависимости.

Модель линейной регрессии является часто используемой и наиболее изученной в эконометрике. А именно изучены свойства оценок параметров, получаемых различными методами при предположениях о вероятностных характеристиках факторов, и случайных ошибок модели. Предельные (асимптотические) свойства оценок нелинейных моделей также выводятся исходя из аппроксимации последних линейными моделями. Необходимо отметить, что с эконометрической точки зрения более важное значение имеет линейность по параметрам, чем линейность по факторам модели.

[править | править исходный текст]

В классической линейной регрессии предполагается, что наряду со стандартным условием E(\varepsilon_t)=0 выполнены также следующие предположения (условия Гаусса-Маркова):

1) Гомоскедастичность (постоянная или одинаковая дисперсия) или отсутствие гетероскедастичности случайных ошибок модели: V(\varepsilon_t)=\sigma^2=const

2) Отсутствие автокорреляции случайных ошибок: \forall i,j,~ i \not = j ~~cov(\varepsilon_i,\varepsilon_j)=0

Данные предположения в матричном представлении модели формулируются в виде одного предположения о структуре ковариационной матрицы вектора случайных ошибок: V(\varepsilon)=\sigma^2 I_n

Помимо указанных предположений, в классической модели факторы предполагаются детерминированными (нестохастическими). Кроме того, формально требуется, чтобы матрица X имела полный ранг (k), то есть предполагается, что отсутствует полная коллинеарность факторов.

При выполнении классических предположений обычный метод наименьших квадратов позволяет получить достаточно качественные оценки параметров модели, а именно: они являются несмещёнными, состоятельными и наиболее эффективными оценками.

13. Показатели тесноты связи. Свойства.

Понятие степени тесноты связи между двумя признаками возникает вследствие того, что в реальной действительности на изменение результативного признака влияют несколько факторов. При этом влияние одного из факторов может выражаться более заметно и четко, чем влияние других факторов. С изменением условий в качестве главного, решающего фактора может выступать другой.

При статистическом изучении взаимосвязей, как правило, учитываются только основные факторы. А вопрос необходимо ли вообще изучать более подробно данную связь и практически ее использовать, решается с учетом степени тесноты связи.

Для характеристики степени тесноты корреляционной связи могут применяться различные статистические показатели: коэффициент Фехнера (КФ), коэффициент линейной (парной) корреляции, коэффициент детерминации, корреляционное отношение, индекс корреляции, коэффициент множественной корреляции, коэффициент частной корреляции и др.

Корреляционно-регрессионный метод анализа

Наиболее простым вариантом корреляционной зависимости является парная корреляция, т.е. зависимость между двумя признаками (результативным и факторным или между двумя факторными). Математически эту зависимость можно выразить как зависимость результативного показателя у от факторного показателя х. Связи могут быть прямые и обратные. В первом случае с увеличением признака х увеличивается и признак у, при обратной связи с увеличением признака х уменьшается признак у.

Непараметрические показатели связи

В статистической практике могут встречаться такие случаи, когда качества факторных и результативных признаков не могут быть выражены численно. Поэтому для измерения тесноты зависимости необходимо использовать другие показатели. Для этих целей используются так называемые непараметрические методы.

Наибольшее распространение имеют ранговые коэффициенты корреляции, в основу которых положен принцип нумерации значений статистического ряда. При использовании коэффициентов корреляции рангов коррелируются не сами значения показателей х и у, а только номера их мест, которые они занимают в каждом ряду значений. В этом случае номер каждой отдельной единицы будет ее рангом.

Коэффициенты корреляции, основанные на использовании ранжированного метода, были предложены К. Спирмэном и М. Кендэлом.

14. Индексы. Методы построения общих индексов. Примеры индексов.

Индексы

Цель: познакомить студентов с важнейшими приемами индексного анализа связи и изменения признаков с разнородными элементами, а также показателей совокупности однородных единиц.

Задачи: характеристика условий формирования системы индексов, методики построения агрегатной формы индексов и средних из индивидуальных, индексов средних величин и территориальных индексов.

Виды индексов. Правила построения индексов

Понятие индекс имеет латинский корень index показывающий, указатель. Распространенное однокоренное слово – индикатор.

В статистике под индексом понимается относительный показатель, характеризующий результат сравнения двух уровней объекта. Можно выделить результаты изменения величины во времени (динамические индексы), в пространстве (территориальные индексы), по отраслям (отраслевые индексы) и другие.

Величина, изменение которой измеряется с помощью индекса, называется индексируемой величиной. Так в индексе цен индексируемой величиной является цена, в индексе физического объема индексируемой величиной является физический объем (объем выпуска в натуральном выражении).

Данные текущего уровня (величина, которая сравнивается) принято обозначать значком «1» (x₁ или x¹), а данные базисного уровня, служащего базой сравнения, обозначаются со значком «0» (x₀ или x⁰).

Индекс строится как отношение индексируемой величины на текущем уровне к значению индексируемой величины на базисном уровне.

По степени охвата элементов явления (представляющих собой единицы совокупности) индексы разделяют на индивидуальные и сводные (общие).

Индивидуальный индекс измеряет изменение отдельного элемента явления (например, изменение объема выпуска телевизоров определенной марки, рост или падение цен на акции в некотором акционерном обществе и т.д.). Индивидуальные индексы обозначаются «i» и снабжаются подстрочным знаком индексируемого показателя: i_q - индивидуальный индекс физического объема определенного вида продукции, i_p – индивидуальный индекс цен на определенный вид продукции и т.д.

Индивидуальные индексы относятся к одному элементу и рассчитываются как отношение двух индексируемых величин:

.

Например, i_p = p₁/p₀ - индивидуальный индекс цен, где p₁,p₀ - цены единицы продукции в текущем (отчетном) и базисном периодах. i_q = q₁/q₀ - индивидуальный индекс физического объема продукции.

Сводный (общий) индекс характеризует изменение всех элементов явления. Например, изменение физического объема продукции предприятия, выпускающего разноименные товары; изменение цены на разные группы товаров и т.д.

Если индексы охватывают не все элементы явления, а лишь часть, то их называют групповыми или субиндексами (например, индексы продукции по отдельным отраслям промышленности).

Сводный индекс обозначается буквой «I» и также сопровождается подстрочным знаком индексируемого показателя: например, Ip - сводный индекс цен; Iz - сводный индекс себестоимости.

Сводные (общие) индексы могут быть построены двумя способами: как агрегатные и как средние из индивидуальных индексов.

Агрегатные индексы - основная форма индексов

Основной формой индексов являются агрегатные индексы.

«Агрегатным» он называется потому, что его числитель и знаменатель представляют собой набор – «агрегат» (от латинского aggregatus – складываемый, суммируемый) элементов, относящихся к изучаемому явлению. Агрегатный индекс строится как отношение сумм произведений двух величин: 1) индексируемой величины - х, которая меняется в числителе по сравнению со знаменателем, 2) соизмерителя (веса индекса) - f, который остается неизменным в числителе и знаменателе. Произведение индексируемой величины на вес индекса (соизмеритель) называют результативным показателем.

( I = ∑x₁f /∑x₀f)

где х1 – сравниваемое (текущее) значение данного признака;

х0 – базисное значение, относящееся к базовому периоду времени, либо базовому объекту сравнения;

j – номер элемента, совокупность которых образует сложное явление (j = 1; J);

х_j·f_j – результативный показатель для i–ого элемента.

Важной особенностью агрегатных индексов является то, что они обладают синтетическими и аналитическими свойствами. Синтетические свойства индексов состоят в том, что посредством индексного метода производится соединение в целое разнородных единиц статистической совокупности. Аналитические свойства определяются тем, что с помощью индексного метода можно оценить влияние факторов на изменение изучаемого показателя.

Важным моментом при построении агрегатных индексов является выбор системы весовых коэффициентов: это могут быть значения на базисном или текущем уровне, плановые значения, нормативные или условные значения. В каждом случае веса должны быть обоснованы и должны соответствовать цели, для которой используется индекс и реальным экономическим условиям.

Если в качестве весов брать значения признака-веса за базисный период времени (или относящиеся к базисному объекту), то формула агрегатного индекса примет вид:

Ее еще называют агрегатной формой индекса Ласпейреса (по имени ученого Э. Ласпейреса, предложившего ее впервые в 1864 г.).

Если в качестве весов брать значения признака-веса за текущий период времени (или относящиеся к текущему объекту), то формула агрегатного индекса примет вид:

Ее еще называют агрегатной формой индекса Пааше (по имени ученого Г.Пааше, предложившего ее впервые в в 1874 г.).

Можно построить общий индекс как среднее геометрическое из индексов Ласпейреса и Пааше:

.

Этот способ предложил Фишер и назвал данную формулу «идеальным индексом».

Различают индексы объемных (количественных) и качественных показателей.

Объемные индексы служат для измерения изменения объемных показателей. Объемные показатели выражаются абсолютными величинами. Например, объем выпуска продукции, численность работающих.

Качественные индексы служат для измерения изменения качественных показателей. Качественный показатель определяется в расчете на количественную единицу. Примером таких показателей могут служить: цена, себестоимость единицы продукции, трудоемкость единицы продукции, производительность труда и т.п.

В качестве веса индекса при построении индекса объемного показателя выступает качественный показатель. Рассмотрим построение агрегатного индекса на примере индекса физического объема.

В данном случае индексируемой величиной будет q – показатель физического объема выпуска продукции в натуральных единицах измерения. Весом индексирования может быть цена – p.

Весом индексирования при построении индекса качественного показателя выступает объемный показатель. Рассмотрим построение агрегатного индекса на примере качественного показателя – p цены за единицу продукции. Весом индекса будет физический объем выпуска (q). Результативный показателем при этом будет общая стоимость произведенной продукции (p·q).

В экономике часто встречаются показатели, определяемые как произведение двух сомножителей, один из которых показатель качественный, другой объемный. Это две стороны одного явления, однако они по разному влияют на результат. Качественный (интенсивный) фактор относится ко всей совокупности. Является средней характеристикой всей объемной величины. Нас интересует результат его влияния в текущем периоде, при фактическом (текущем) объеме и изменение качественного показателя оценивается на фоне текущего значения объемной величины.

Изменение объемного (экстенсивного) показателя оценивается на фоне базисного уровня качественного фактора.

Такой порядок исчисления индексов и определения степени влияния факторов на результат относится ко всем случаям взаимосвязанных показателей, когда результирующий показатель есть произведение двух факторов, один из которых качественный, другой - объемный. Например, общие затраты на производство в денежных единицах - z∙q (z-себестоимость единицы продукции, q – показатель физического объема выпуска продукции в натуральных единицах измерения), затраты времени на производство данного объема продукции – t∙q (t-трудоемкость единицы продукции).

Рассмотрим построение индексов для случая взаимосвязанных показателей для стоимости продукции S, цены за единицу продукции p и физического объема продукции q.

Индивидуальные индексы показателей имеют вид:

- физического объема работ или услуг

i_q = q¹/q⁰,

- цены

i_p =p¹/p⁰,

- стоимости

i_pq =p¹q¹/p⁰q⁰ или i_s =p¹q¹/p⁰q⁰

Агрегатный индекс физического объема работ или услуг (индекс объемного показателя) строится как индекс Ласпейреса по базисным ценам (p₀):

Агрегатный индекс цен (индекс качественного показателя) строится как индекс Пааше по текущим значениям физического объема (q₁):

Сводный индекс результативного показателя представляет собой отношение суммы результативных показателей текущего периода (объекта) к сумме результативных показателей базисного периода (объекта):

.

Например, отношение стоимости продукции отчетного (текущего) периода S₁=q₁·p₁ к стоимости продукции базисного периода S₀=q₀·p₀ представляет собой сводный индекс стоимости продукции или товарооборота:

или I_s = ∑ q₁·p₁/∑ q₀·p₀.

Этот индекс показывает во сколько раз в среднем возросла (уменьшилась) стоимость продукции (товарооборота) отчетного периода по сравнению с базисным.

Рассмотрим пример. Имеются данные о фактическом выпуске и ценах на продукцию машиностроительным предприятием за два года (табл. 6.1). Необходимо рассчитать сводные и индивидуальные индексы.

Таблица 6.1

Данные о фактическом выпуске и ценах на продукцию машиностроительного предприятия

Виды продукции	Выпуск продукции в натуральном выражении		Цена производителя за единицу, млн.руб.		Индивидуальные индексы физического объема продукции: iq=q1/q0	Индивидуальные индексы цен: ip=p1/p0	Индивидуальный индекс стоимости: ipq=p1·q1/p0·q0
	Базисный период q0	Отчетный период q1	Базисный период p0	Отчетный период p1
1	2	3	4	5	6	7	8
1	40	60	30	35	1,5	1,1(6)	1,75
2	50	70	80	70	1,4	0,875	1,225
3	60	80	50	50	1,(3)	1	1,(3)

Расчет индивидуальных индексов приведен в таблице (столбцы 6, 7, 8).

Общий индекс физического объема:

.

В целом по трем видам продукции наблюдается рост физического объема выпуска за рассматриваемый период на 39%.

Общие индексы цены:

.

В целом по трем видам продукции наблюдается снижение цен за рассматриваемый период на 3,5%.

Общие индексы стоимости:

.

В целом по трем видам продукции за рассматриваемый период стоимость возросла на 34%.

Средние (арифметические и гармонические) индексы на основе индивидуальных индексов: их связь с агрегатными индексами

Сводный индекс может быть построен как средняя взвешенная величина из индивидуальных индексов. Выбор вида средней (арифметическая или гармоническая) зависит от используемых весовых коэффициентов. При этом значение среднего индекса должно совпадать со значением агрегатного индекса (Ласпейреса или Пааше). Весами усреднения выступают в данном случае результативные показатели (либо базисного, либо текущего уровня): _j=x_j·f_j.

; .

Вид степенной средней зависит от имеющейся в нашем распоряжении информации.

Если имеются данные об индивидуальных индексах i_xj и о значении результативного показателя за базисный период времени (либо относящиеся к базисному объекту) 0_j = x0_j · f0_j, то усреднение происходит по формуле средней арифметической взвешенной с весами равными результативному показателю базисного периода. Данный индекс тождественен агрегатной форме индекса Ласпейреса:

Если имеются данные об индивидуальных индексах i_xj и о значении результативного показателя за текущий период времени (либо относящиеся к текущему объекту) 1_j = x1_j · f1_j, то усреднение происходит по формуле средней гармонической взвешенной с весами равными результативному показателю текущего периода. Данный индекс тождественен агрегатной форме индекса Пааше:

В качестве весов могут приниматься не только абсолютные значения результативного показателя, но и относительные величины - доли, проценты результативного показателя отдельной единицы (элемента) в общем объеме результативного показателя по совокупности (явлению) в целом:

, ;

, .

Если строятся сводные индексы качественных показателей, то используется формула среднего гармонического взвешенного по текущим значениям результата. Так сводный индекс цен определяется как среднее гармоническое из индивидуальных индексов цен (i_p), взвешенное по текущей (фактической) стоимости (p₁q₁):

При построении сводных индексов объемных показателей используется формула среднего арифметического взвешенного по базисным значениям результата. Сводный индекс физического объема продукции рассчитывается как среднее арифметическое из индивидуальных индексов (i_q), взвешенное по базисной стоимости (p₀q₀):

.

По данным нашего примера (таблицы) рассчитаем сводные индексы физического объема и цены как средние из индивидуальных.

Сводный индекс физического объема продукции:

.

Сводный индекс цен:

Значения индексов, рассчитанных как агрегатные и как средние из индивидуальных, совпали.

Индексный метод используется для определения влияния различных факторов на изменение результата как в относительном, так и в абсолютном выражении.

Некоторые экономические показатели находятся между собой в определенной (функциональной) связи, например, в виде произведения (либо отношения). В таком же соотношении должны находиться и статистические показатели, характеризующие изменение исходных экономических показателей, т.е. индексы: если z = x · y , то I_z = I_x · I_y

Для индивидуальных индексов это очевидно:

При построении сводного индекса соотношение I_z=I_x·I_y осуществимо, если веса индексирования для I_x и I_y берутся за разные периоды времени (или относятся к разным объектам), т.е. один из индексов должен быть построен по формуле Ласпейреса, а другой - по формуле Пааше:

.

Если один из сомножителей показатель качественный, а другой - объемный, то, как уже было отмечено, индекс качественного показателя определяется по текущим значениям объемного показателя.

Общая стоимость продукции равна произведению цены за единицу продукции на физический объем выпуска: ∑S = ∑p·q. Тогда сводный индекс стоимости должен быть равен произведению сводного индекса цен на сводный индекс физического объема I_s = I_p·I_q. Чтобы выполнялось данное условие необходимо, чтобы веса при построении индексов цен и физического объема относились к разным уровням. Принято вычислять индекс цен по формуле Пааше, а индекс физического объема по формуле Ласпейреса:

.

При этом I_s показывает общее изменение стоимости, индекс цены I_p – как изменилась стоимость за счет изменения цен, а I_q – как изменилась стоимость за счет изменения физического объема продукции.

В нашем примере (табл. 6.1) общий индекс стоимости:

Таким образом, стоимость продукции выросла на 34 %, в том числе за счет увеличения объема выпуска продукции на 39 %, а в связи со снижением цен снизилась на 3,5 %.

Индексный метод анализа влияния факторов

Индексный метод позволяет также представить абсолютное изменение результативного показателя (z), как результат влияния различных факторов (входящих в формулу его расчета).

Общее абсолютное изменение результативного показателя текущего уровня по сравнению с базисным определяется как разница между числителем и знаменателем в формуле соответствующего аналитического сводного индекса данного результативного показателя.

Абсолютный прирост стоимости продукции может быть представлен как:

.

И разложен на:

1. абсолютный прирост стоимости за счет изменения цен:

.

2. абсолютный прирост стоимости за счет изменения количества выпускаемой продукции:

.

Общее абсолютное изменение стоимости продукции равно алгебраической сумме изменений за счет каждого из факторов:

s = s_p + s_q .

По данным рассмотренного примера стоимость продукции составила в базисном периоде s₀ = ∑p₀q₀ = 8200 тыс.руб., в текущем периоде s₁ = ∑p₁q₁ =11000 тыс.руб., стоимость продукции текущего периода по базисным ценам ∑p₀q₁ = 11400 тыс.руб.

Общее изменение стоимости продукции s = s₁ - s₀ = 11000 – 8200 = 2800 тыс.руб.

В том числе за счет:

- изменения цен s_p = ∑p₁q₁ - ∑p₀q₁ = 11000 – 11400 = -400 тыс. руб. стоимость продукции уменьшилась на 400 тыс.руб.

- за счет изменения объема выпуска продукции s_q = ∑p₀q₁ - ∑p₀q₀ = 11400–8200=3200 тыс.руб. стоимость продукции выросла на 3200 тыс.руб.

Пусть по предприятию имеются данные о выпуске продукции Q и численности работающих T за два периода времени. В базисном периоде выпуск продукции составил 20000 тыс.руб., число работающих – 200 чел., в текущем периоде выпуск продукции составил 23100 тыс.руб., число работающих – 220 чел. Необходимо проанализировать изменение выпуска продукции.

Уровень производительности труда (выработка на одного работающего) в базисном периоде W₀ = Q₀/T₀ = 100 тыс.руб./чел., в текущем периоде W₁ = Q₁/T₁= 23100/220 = 105 тыс.руб./чел.

По каждому показателю рассчитаем индексы и абсолютные приросты, данные сведены в табл. 6.2.

Таблица 6.2

Анализ влияния факторов на изменение объема выпуска

	Базисный период	Текущий период	Абсолютный прирост (∆)	Индекс (i)
Q	20000	23100	+3100	1,155
T	200	220	+20	1,1
W	100	105	+5	1,05

I_Q = 1,1 · 1,05 = 1,155 = 115,5 %.

Таким образом, объем продукции увеличился на 15,5 %, в том числе:

• за счет роста затрат труда на 10 % - экстенсивный фактор;

• за счет роста производительности труда на 5 % - интенсивный фактор.

Общее изменение выпуска продукции в абсолютном выражении:

В том числе за счет увеличения затрат труда (экстенсивный фактор оценивается по базисному значению качественного фактора W₀):

За счет повышения производительности труда (качественный, интенсивный фактор оценивается по текущему значению объемного фактора T₁):

Общее изменение: 2000 + 1100 = 3100 .

Индексы постоянного и переменного состава. Индекс среднего уровня и учет в нем изменения структуры; индекс структурного сдвига

Индексный метод используется и в анализе средних величин. В отличие от агрегатных данные индексы рассчитываются по качественно однородным совокупностям, состоящим из сопоставимых элементов.

Индекс средней цены (качественного признака):

_.

Если принять - удельный вес количества группы в общем количестве, получим:

На величину индекса средней цены влияет как изменение цен, так и изменения структуры набора продукции, для которой определялась средняя цена, поскольку в ее расчете участвуют веса разных периодов (q₀ и q₁) и (u₀ и u₁). Поэтому индекс средней величины называется индексом переменного состава. Индекс переменного состава показывает, как изменилось среднее значение признака.

Для анализа влияния непосредственного изменения цен рассчитывают индекс постоянного (фиксированного) состава:

_.

Индекс постоянного состава показывает как изменилось среднее значение признака за счет изменения самого признака, то есть изменение средней цены на продукцию за счет изменения цен.

Для определения влияния изменения структуры продукции рассчитывается индекс структурного сдвига:

_.

Индекс структурного сдвига показывает как изменилось среднее значение признака в связи с изменением структуры, то есть изменение средней цены на продукцию за счет изменения удельных весов в общем объеме продукции групп с разным уровнем цены за единицу продукции.

Индексы переменного состава, постоянного состава и структурного сдвига связаны между собой:

Данный метод применим для оценки влияния структурных сдвигов на изменение средних значений качественных показателей (производительности труда, среднего заработка, себестоимости единицы продукции и других).

Таблица 6.3

Анализ изменения средней себестоимости

Пред- приятие	Выпуск продукции, тыс. единиц		Себестоимость единицы продукции, тыс. руб.		Доля предприятия в общем выпуске
	базисный q0	текущий q1	базисная z0	текущая z1	базисная u0	текущая u1
№1	50	200	50	60	0,25	0,80
№2	150	50	25	30	0,75	0,20
Сумма	200	250	х	х	1,00	1,00

Пусть, однородная продукция выпускается на двух предприятиях отрасли. Данные по предприятию приведены в табл. 6.3.

Индекс средней себестоимости (индекс переменного состава):

.

Средняя себестоимость выросла в 1,73 раза или на 72,8 %.

.

За счет роста себестоимости на предприятиях средняя себестоимость единицы продукции выросла в 1,2 раза или на 20%., или себестоимость единицы продукции увеличилась в среднем на 20%.

Индекс структурного сдвига:

или

За счет изменения структуры выпуска продукции средняя себестоимость выросла на 44%. Увеличилась доля выпуска продукции с 0,25 до 0,8 на предприятии №1 с более «дорогой» продукцией, что и повысило среднюю себестоимость на 44%.

Особенности построения индексов экономических показателей

В разделах экономической статистики рассматриваются индексы конкретных экономических показателей. Однако, нужно сделать несколько замечаний.

Одним из важнейших показателей статистики цен является индекс потребительских цен (ИПЦ). При расчете ИПЦ производится отбор товаров (услуг), по которым производится регистрация цен. Он производится в соответствии с общероссийским классификатором экономической деятельности, продукции и т.д. Затем формируется структура весов по отдельным группам товаров и услуг для расчета сводного индекса потребительских цен. Для этого используются данные о структуре потребительских расходов населения.

Пересчет важнейших стоимостных показателей системы национальных счетов из фактических цен в сопоставимые осуществляется с помощью индекса – дефлятора. Дефлятор – это коэффициент, переводящий значение стоимостного показателя за отчетный период в стоимостные измерители базисного.

Для расчета индекса Пааше требуется взвешивание по весам отчетного периода, что в масштабах страны требует очень больших затрат. Начиная с 1991 года индекс цен в России определяется как индекс Леспейреса. При этом весовые коэффициенты по выпуску продукции фиксируются на уровне базисного периода и остаются неизменными в течение некоторого промежутка времени. Целью расчета индекса является измерение динамики стоимости базисного (неизменного) объема продукции. Чем дальше от базисного периода, тем менее надежен расчетный индекс цен. Система весов должна вовремя пересматриваться.

15. Метод цепных подстановок. Индексы в анализе средних величин.