8.Расчет винтовых цилиндрических пружин.

Пружины являются одним из наиболее широко распространенных упругих элементов современных механизмов и машин. Их используют главным образом в качестве амортизаторов — для смягчения ударов и толчков. В ряде случаев пружины используются в качестве аккумуляторов энергии, для приведения в движение отдельных деталей или механизмов. Наибольшее применение получили цилиндрические винтовые пружины, работающие на растяжение или сжатие, изготовляемые из прутков круглого поперечного сечения. Ниже дан приближенный расчет таких пружин.

Рассмотрим пружину, нагруженную по концам растягивающими силами   действующими вдоль оси пружины и направленными в противоположные стороны (рис. 15.6, а).

Обозначим   радиус пружины, равный расстоянию от центра тяжести поперечного сечения прутка пружины до ее оси, и  — диаметр сечения прутка.

Рассечем мысленно пруток плоскостью, проходящей через ось пружины, и отбросим нижнюю часть пружины. Верхняя часть будет находиться в равновесии под действием внешней силы Р и внутренних усилий в проведенном сечении прутка, заменяющих влияние отброшенной нижней части пружины на верхнюю.

Из условия равновесия оставленной верхней части следует, что равнодействующая указанных внутренних усилий представляет собой силу S, направленную вниз вдоль оси пружины и равную Р (рис.

15.6, б). Эту силу можно заменить вертикальной силой   (приложенной в центре сечения прутка) и моментом  действующими в плоскости проведенного сечения прутка (рис. 15.6, в).

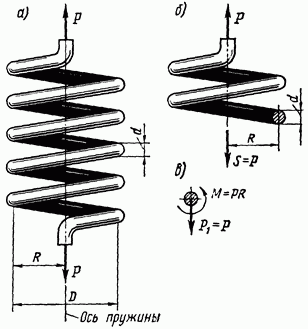
Рис. 15.6

Для упрощения дальнейшего расчета будем предполагать, что угол наклона витков пружины к ее оси близок к 90°.

Это предположение допустимо для пружин, у которых указанный угол не менее 75° (обычно он равен 80-85). Оно позволяет рассматривать сделанное выше сечение прутка (рис. 15.6,б) как поперечное, момент   как крутящий момент   а силу   — как поперечную силу 

Сила   вызывает в сечении касательные напряжения  ; приближенно будем считать эти напряжения распределенными равномерно по всему сечению прутка:

Эпюра касательных напряжений показана на рис. 16.6, а. Кроме того, в сечении прутка возникают касательные напряжения   связанные с наличием крутящего момента   и равные [на основании формулы (7.6)]

Эпюра касательных напряжений   показана на рис. 16.6, б.

Наибольшие напряжения   возникают у боковой поверхности прутка, где они равны

Напряжения   в каждой точке сечения направлены по нормали к прямой, соединяющей данную точку с центром сечения прутка. Суммарное напряжение   от поперечной силы Q и крутящего момента   в каждой точке сечения прутка можно определить путем геометрического сложения напряжений   (рис. 16.6, в). В точке С сечения прутка, наиболее близко расположенной к оси пружины, напряжения   и совпадают по направлению и, кроме того, значение   в этой точке максимально.

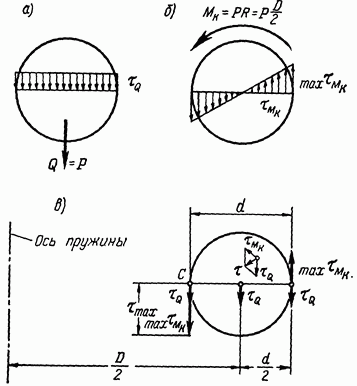
Рис. 16.6

Таким образом, суммарное напряжение   в точке С имеет наибольшее значение

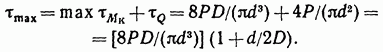
Обычно второе слагаемое в круглых скобках формулы (25.6) значительно меньше единицы (в большинстве случаев   и, следовательно,  ) и им можно пренебречь; это равносильно пренебрежению напряжениями от поперечной силы по сравнению с напряжениями от кручения. Тогда формула (25.6) примет вид

Из формулы (26.6) следует, что увеличение диаметра пружины уменьшает, а увеличение диаметра прутка увеличивает ее прочность.

Для обеспечения прочности пружины величина   не должна превышать величины допускаемого напряжения   Пружины изготовляются из высококачественной стали; поэтому значения допускаемых напряжений весьма высоки: 

Условие прочности пружины имеет вид

Формулы (26.6) и (27.6) являются приближенными. Используя результаты, полученные при определении напряжений в пружинах уточненными методами, условие прочности можно представить в виде

где k — поправочный коэффициент, определяемый на основе точных методов расчета пружин. Его значение можно вычислять по формуле

Рассмотрим теперь деформацию пружины, т. е. изменение ее длины в направлении оси пружины. Обозначим X деформацию пружины под действием двух сил Р, приложенных по концам и направленных вдоль ее оси в противоположные стороны.

Работа статически приложенных сил Р на перемещении, равном деформации  , определяется из выражения

Потенциальную энергию U деформации пружины, вызванной силами Р, определяем только от крутящих моментов  возникающих в поперечных сечениях прутка пружины. Влиянием сил   на деформацию пружины пренебрегаем. По формуле (16.6):

где  -длина прутка пружины;   — число витков пружины.

На основании закона сохранения энергии   следовательно,

откуда

Величина усилия Р, при которой деформация   пружины равна единице (1 мм, 1 см и т. п.), называется жесткостью пружины и обозначается С. Из (30.6) следует

и

Жесткость пружины измеряется в   и т. п.

Из формул (30.6) и (31.6) следует, что увеличение числа витков   пропорционально увеличивает деформацию пружины К и, следовательно, уменьшает ее жесткость; увеличение диаметра прутка повышает жесткость пружины, а увеличение диаметра пружины понижает ее.