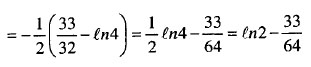- •Вища математика, 3 семестр. Файл для читання
- •12.6.1. Основні поняття
- •Розділ 12: Кратні інтеграли
- •12.1. Інтеграли по області, їх властивості, різновиди.
- •12.2 Обчислення криволінійних інтегралів першого роду
- •12.3.1 Обчислення подвійних інтегралів
- •12.3.2. Заміна змінних в подвійному інтегралі
- •12.4. Обчислення поверхневих інтегралів і-го роду
- •12.5 Обчислення потрійних інтегралів
- •12.5.1 Основні поняття
- •12.5.2. Заміна змінних в потрійному інтегралі
- •12.6 Невластиві інтеграли по області
- •12.6.1 Основні поняття
- •Розділ 13: Теорія поля
- •13.1. Визначення полів та їх характеристики
- •Характеристики векторного поля
- •7 Вихор векторного поля є вектором, який характеризує поверхневу щільність циркуляції, позначають rot , визначають формулою:
- •13.2. Обчислення криволінійних та поверхневих інтегралів другого роду
- •13.2.1. Знаходження криволінійних інтегралів
- •13.2.2. Знаходження поверхневих інтегралів другого роду
- •13.3. Властивості векторних полів
- •13.3.1. Соленоїдальність, потенціальність та безвихорність.
- •13.3.2. Формули Остр.-Гаусса, Стокса та Гріна
- •13.4. Оператори Гамільтона та Лапласа.
- •13.4.1. Оператор Гамільтона та його застосування.
- •Основні правила застосування оператора
- •13.4.2. Оператор Лапласа
- •13.4.3. Диференціальні операції другого порядку теорії поля.
- •Розділ 14: Числові ряди.
- •14.1 Необхідна ознака збіжності ряду.
- •14.2. Достатні ознаки збіжності додатних числових рядів
- •14.2.2 Ознака Даламбера
- •14.2.3. Радикальна ознака Коші.
- •14.2.4 Інтегральна ознака Коші.
- •14.4 Знакозмінні числові ряди
- •14.4.1 Поняття абсолютної та умовної збіжності ряду.
- •14.4.2 Властивості збіжних рядів
- •Розділ 15. Функціональні та степеневі ряди
- •15.1 Функціональні ряди.
- •Властивості правильно збіжних функц. Рядів
- •Різновиди збіжності функціональних рядів
- •15.2 Степеневі ряди
- •15.2.1. Область збіжності та властивості:
- •15.2.2. Розклад функції в степеневий ряд
- •Формули:
- •Приклади
- •Розділ 16: Гармонічний аналіз (Фур’є only)
- •16.2 Ряди Фур’є. Розклад функції в ряд Фур’є.
- •16.3.Перетворення Фур’є.
- •Основні властивості перетворення Фур’є.
- •Розділ 17: Перетворення Лапласа та його властивості
- •17.1. Теоретичні відомості.
- •Оригінали та зображення
- •Одинична функція Хевісайда та її зображення.
- •17.2 Властивості зображень Лапласа
- •17.4. Визначення оригіналу за його зображенням Лапласа.
- •Розділ 18: Основи теорії функції комплексної змінної
- •18.1.Форми запису комплексних змінних та дії з ними
- •Дії з комплексними числами.
- •18.1.2. Область на комплексній площині
- •18.2. Послідовності та функції комплексної змінної
- •18.2.1. Послідовності комплексних чисел та їх границі.
- •18.2.2. Функції комплексної змінної.
- •18.2.3. Границя та неперервність функції комплексної змінної.
- •18.2.4. Основні трансцендентні функції.
- •18.3. Диференційованість та аналітичність функцій
- •18.3.1 Диференціювання функції комплексної змінної
- •18.3.2 Аналітичність функції
- •18.3.3 Електростатичний смисл аналітичної функції
- •18.4. Інтегрування функцій комплексної змінної.
- •18.4.1. Означення та властивості інтеграла.
- •18.4.2. Інтегральні теореми Коші.
- •18.5. Числові, функціональні та степеневі ряди.
- •18.5.1. Ряди з комплексними числами.
- •18.5.2 Функціональні та степеневі ряди.
- •18.5.4 Розклад в ряд Тейлора.
- •18.6. Ряди Лорана
- •18.7 Особливі точки та інтегральні лишки аналітичних функцій
- •18.8 Обчислення інтегралів з використанням лишків
- •18.10. Поняття конформного відображення.
- •Розділ 19: Рівняння математичної фізики. Класифікація диференціальних рівнянь другого порядку з частинними похідними
- •19.1. Поняття диференціального рівняння з частинними похідними
- •19.2. Класифікація лінійних диференціальних рівнянь з частинними похідними другого порядку з двома незалежними змінними
- •19.3. Зведення до канонічного вигляду диференціальних рівнянь з частинними похідними другого порядку з двома незалежними змінними
- •Розділ 20: Операційне числення
12.3.2. Заміна змінних в подвійному інтегралі
При заміні змінних : x = φ (u,v), y = ψ (u,v) область D площини xOy відображається в область G площини uOv; елемент площини dxdy відобразиться в елемент площі
|
I(u,v)
|dudv
,
де визначник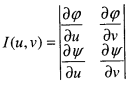 називають
функціональним визначником або
якобіантом, а його модуль називають
коефіцієнтом спотворення області. Отже,
якщо функції φ
(u,v)
та ψ (u,v)
неперервні в області G
разом із своїми частинними похідними
першого порядку, то має місце рівність:
називають
функціональним визначником або
якобіантом, а його модуль називають
коефіцієнтом спотворення області. Отже,
якщо функції φ
(u,v)
та ψ (u,v)
неперервні в області G
разом із своїми частинними похідними
першого порядку, то має місце рівність:
![]() Часто
для обчислення подвійних інтегралів
використовують полярні координати: x
= rcos
, y
= rsinφ
. Тоді якобіан переходу I(r,
φ)=r,
а елемент площі dxdy
= rdrdφ.
Часто
для обчислення подвійних інтегралів
використовують полярні координати: x
= rcos
, y
= rsinφ
. Тоді якобіан переходу I(r,
φ)=r,
а елемент площі dxdy
= rdrdφ.
Перехід в подвійному інтегралі до полярних координат доцільно використовувати в тих випадках, коли підінтегральна функція залежить від x2+y2 або від arctg(y/x), а також у випадках, коли межа області містить дуги кіл та промені ,що виходять із початку координат.
Приклад:
Обчислити інтеграл
![]() по чверті кільця
по чверті кільця
![]() що
лежить в першому квадранті.
що
лежить в першому квадранті.
Розвязання: Область інтегрування D зобразимо на малюнку:
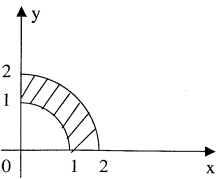
Підставимо
в нерівність
![]() замість
x
та y
їх значення
замість
x
та y
їх значення
x
= rcos
, y
= rsinφ
. Одержимо:
![]() Оскільки кільце лежить
Оскільки кільце лежить
в
першому квадранті ,то
![]() Отже:
Отже:
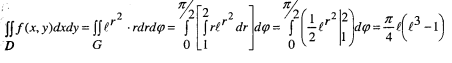
12.4. Обчислення поверхневих інтегралів і-го роду
Поверхне́вий інтегра́л — це визначений інтеграл, котрий береться по поверхні (яка може бути зігнутою множиною в просторі); його можна розглядати як подвійний інтегральний аналог лінійного інтегралу
Я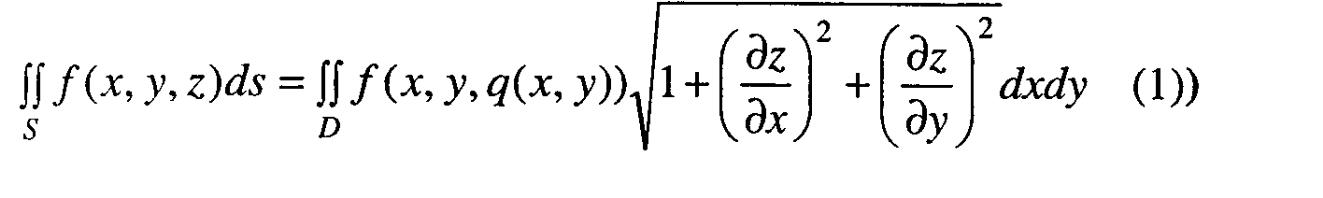 кщо
S – незамкнена
поверхня, яка задається рівнянням z
= q(x,y),
а область D-
проекція цієї поверхні на площину хОу,
тоді
кщо
S – незамкнена
поверхня, яка задається рівнянням z
= q(x,y),
а область D-
проекція цієї поверхні на площину хОу,
тоді
Я![]()
![]()
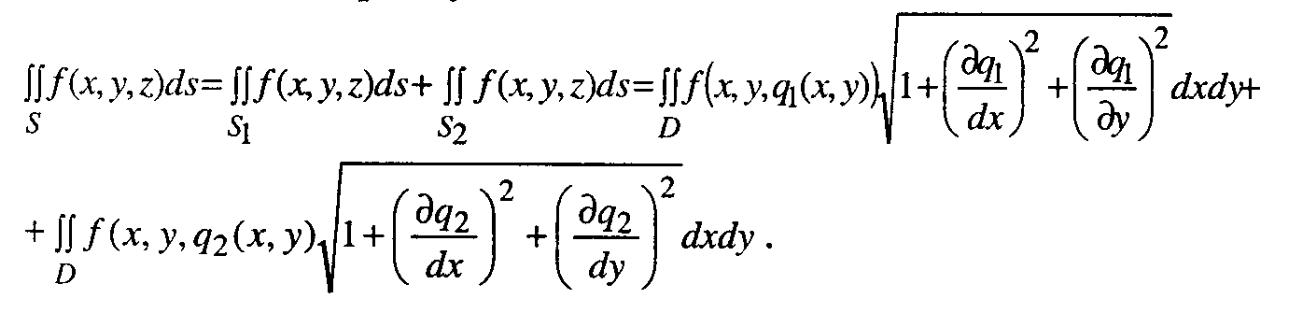 кщо
поверхня S
– замкнена,
тоді її розбивають на дві незамкнені
кщо
поверхня S
– замкнена,
тоді її розбивають на дві незамкнені ![]() так, щоб обидві вони
проектувалися на одну область D площини
xOy. Якщо рівнянням поверхні
а рівнянням поверхні
тоді
так, щоб обидві вони
проектувалися на одну область D площини
xOy. Якщо рівнянням поверхні
а рівнянням поверхні
тоді

П риклад
1
Обчислити де S –
частина площини х+у+z = 1,
яка лежить в першому октанті(мал.5)
риклад
1
Обчислити де S –
частина площини х+у+z = 1,
яка лежить в першому октанті(мал.5)
Розвязання В даному випадку рівнянням поверхні S буде z = 1-x-y, її проекцію – областю D буде прямокутний трикутник обмежений лініями: х=0, y=0, x+y=1
П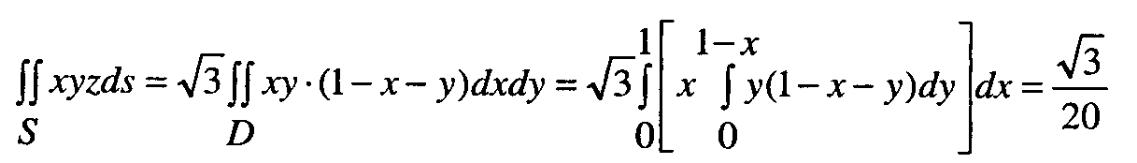 оверхня
S
– незамкнена,
тому за формулою(1) одержимо
оверхня
S
– незамкнена,
тому за формулою(1) одержимо
![]() Приклад
2
Обчислити площу поверхні еліпсоїда
обертання
Приклад
2
Обчислити площу поверхні еліпсоїда
обертання
![]()
Р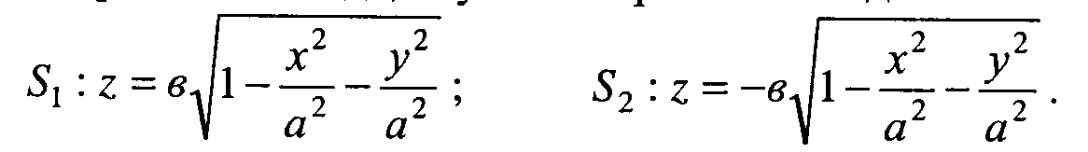 озв'язання
Згідно властивості інтеграла по області
д де S є поверхня еліпсоїда ,
яку можна розбити на дві частини
озв'язання
Згідно властивості інтеграла по області
д де S є поверхня еліпсоїда ,
яку можна розбити на дві частини
П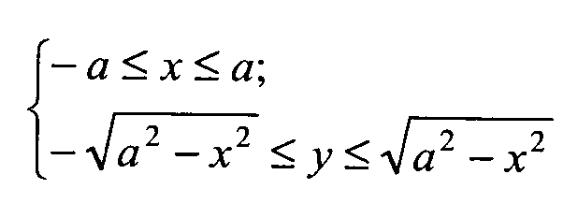 роекцію
цих поверхонь на площину хОу буде круг
D, який визначається системою рівнянь
роекцію
цих поверхонь на площину хОу буде круг
D, який визначається системою рівнянь
![]()
Використовуючи симетрію еліпсоїда отримуємо
Оскільки
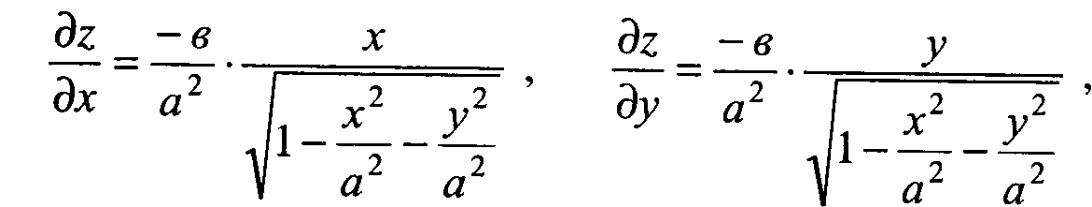
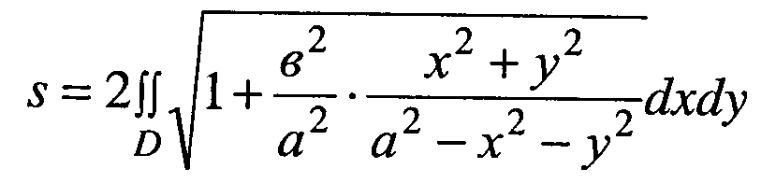
То
П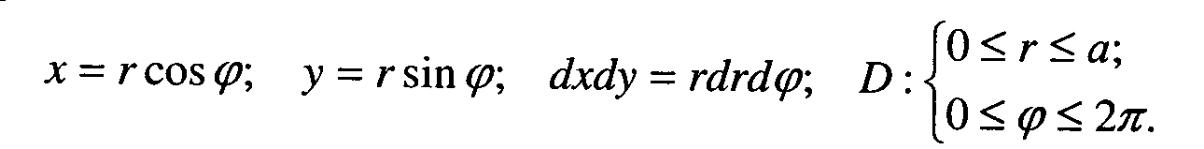 ерейдемо
до полярних координат в подвійному
інтегралі
ерейдемо
до полярних координат в подвійному
інтегралі
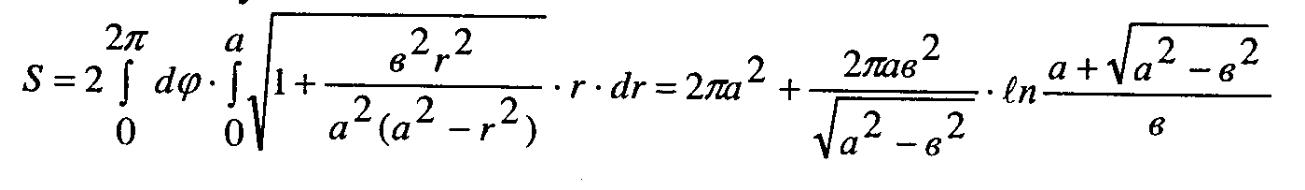
Тому
12.5 Обчислення потрійних інтегралів
12.5.1 Основні поняття
Н ехай
V – деяка просторова область замкнута
поверхнею S,область
V- назив. правильною
за напрямом осі Oz, якщо:
ехай
V – деяка просторова область замкнута
поверхнею S,область
V- назив. правильною
за напрямом осі Oz, якщо:
Будь-яка пряма паралельна осі Oz перетинає поверхню S не більше ніж в двох точках
Вся область V проектується на площину хОу в правильну двовимірну область D.
Область V правильна за напрямком всіх трьох координатних осей назив. правильною.
Я![]()
![]() кщо
тривимірна область правильна, то
обмежуючу її поверхню S можна розбити
на 2 частини
кщо
тривимірна область правильна, то
обмежуючу її поверхню S можна розбити
на 2 частини
![]()
![]()
О![]() бидві
ці площини проектуються на площину хОу
в правильну область D, межа якої точками
а і в поділяється на 2 криві з рівняннями
бидві
ці площини проектуються на площину хОу
в правильну область D, межа якої точками
а і в поділяється на 2 криві з рівняннями
П![]()
![]()
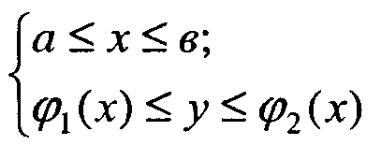 означимо
довільну точку області V
як M(x,y,z),
а її проекцію на площину хОу -
N(x,y,0).
При фіксованих х та у апліката z точки
M,
що знаходиться внутрі області області
V може змінюватися від до
Якщо точка N
пересувається всередині області D
,
а її координати мають задовольняти
означимо
довільну точку області V
як M(x,y,z),
а її проекцію на площину хОу -
N(x,y,0).
При фіксованих х та у апліката z точки
M,
що знаходиться внутрі області області
V може змінюватися від до
Якщо точка N
пересувається всередині області D
,
а її координати мають задовольняти
Т ому
аналітичний опис області V буде такий:
ому
аналітичний опис області V буде такий:
Отже, аналітичний опис області V виглядає так: межі зовнішнього інтегралу – сталі, межі середнього інтегралу – можуть залежати від змінної інтегрування зовнішнього інтегралу(х), межі внутрішнього інтегралу – можуть залежати від інтегрування середнього та зовнішнього інтегралів (х,у)
В цьому випадку обчислення потрійного інтегралу обчислюється шляхом послідовного обчислення інтегралів меншої кратності за формулою:
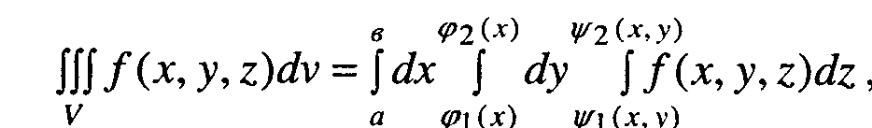
Також використовують ще такі формули:
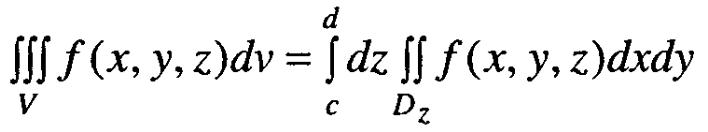
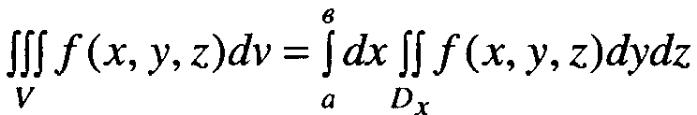
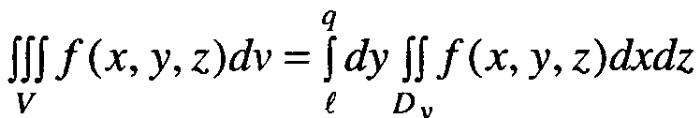
П![]() риклад
1.
Обчислити , де область V
обмежена
поверхнею обертання кривої
риклад
1.
Обчислити , де область V
обмежена
поверхнею обертання кривої
 навколо
осі Oz
і
площиною
навколо
осі Oz
і
площиною
 .
.
Р![]() озв’язання.
Щоб одержати рівняння поверхні обертання
заданої лінії навколо осі Oz,
залишимо змінну z
в рівнянні лінії
без зміни, а у замінимо на
озв’язання.
Щоб одержати рівняння поверхні обертання
заданої лінії навколо осі Oz,
залишимо змінну z
в рівнянні лінії
без зміни, а у замінимо на
 .
.
Одержимо: - рівняння параболоїда обертання.
Проекцією
області V
на
площину xOy
буде
круг

Застосуємо формулу:
![]()
де
Dz
є
перетин області V
площиною,
яка перпендикулярна до осі Oz
і
лежить на висоті z,
причому

П![]() еретин
Dz
буде
кругом радіусом
еретин
Dz
буде
кругом радіусом
 ,
що
випливає із рівняння поверхні обертання
,
що
випливає із рівняння поверхні обертання
 .
.
Внутрішній інтеграл оскільки він дорівнює площі круга. Отже,
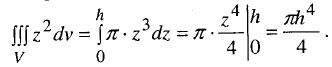
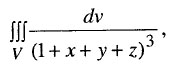
П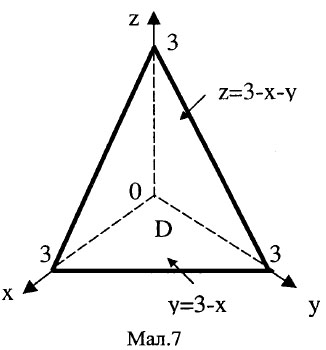 риклад
2.
Обчислити інтеграл
якщо
область V
обмежена
поверхнями
риклад
2.
Обчислити інтеграл
якщо
область V
обмежена
поверхнями

Розв’язання. Область інтегрування V зобразимо на мал. 7.
Визначимо аналітичний опис заданої області V.
Для визначення меж змінної z проведемо через область V пряму,
яка паралельна осі Oz.
Тоді
одержимо:
 .
.
Для
опису області D
виберемо
сталі межі зміни x:

Тоді
у буде змінюватись в межах:

Отже, область V має аналітичний опис: