18.5.4 Розклад в ряд Тейлора.

Аналітичну функцію f(z) в кожній внутрішній точці її області аналітичності D можна розкласти в ряд Тейлора за формулою 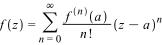(42)

радіус збіжності якого дорівнює відстані від точки а до найближчої до а особливої точки (точки, де функція f(z) не є аналітичною).

Якщо функція f(z) розкладається в степеневий ряд в околі точки z=a

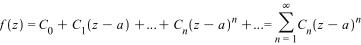(43),

то цей ряд буде її рядом Тейлора, коефіцієнти якого знаходять за формулами: 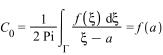та 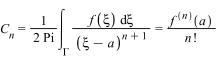n= 1,2…

Якщо в розкладі (43) _,

то точку а називають т кратним нулем функції f(z).

В околі точки а, яка є m кратним нулем функції f(z), функцію можна представити у вигляді _{, де}

є аналітичною функцією в точці а і _.

Найчастіше використовують наступні розклади функцій комплексної змінної в ряд Тейлора

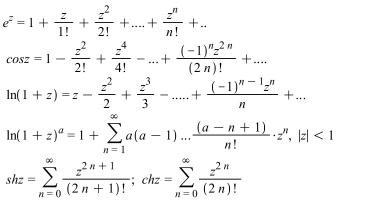
_{Приклад}. Знайти ряд Тейлора функції

Розв’язання. Перетворення 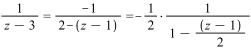дозволяє розкласти як суму нескінченної геометричної прогресії із знаменником _.. Тому .

Круг збіжності цього розкладу Точка є особливою точкою функції f(z), яка лежить на колі круга збіжності.

18.6. Ряди Лорана

Аналітична в кільці ф-ія f(z) у всіх точках кільця розкладається в ряд Лорана (рЛ) коефіцієнти якого обчислюються за ф-лами , де Y - будь-яке коло з центром в точці ,що лежить всередині кільця.

Ряд 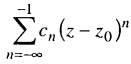називають головною частиною рЛ. Він збігається у всіх точках частини площини, що лежать поза внутрішнім колом кільця .

Ряд називають правильною частиною рЛ. Цей ряд є степеневим рядом Тейлора, що зберігається у всіх точках всередині круга, обмеженого зовнішнім колом кільця .

Кільце є перерізом областей збіжності правильної і головної частин рЛ. У всіх точках кільця збіжності рЛ абсолютно збіжний. РЛ можна почленно інтегрувати по будь-якому колу, концентричному до кіл, що обмежують кільце збіжності, його можна диференціювати почленно скільки завгодно (n) разів всередині кільця збіжності.

Розкладання аналітичної ф-ії f(z) в кільці в рЛ – єдине.

Деякі способи розкладання фій в рЛ. Для дробово-раціональних ф-ій. В цьому випадку розкладання в рЛ зводится до розкладання в ряд геометричнох прогресії ф-ій вигляду: .

Приклад: Розкласти в рЛ ф-ію в областях:

Розкладуючи на елементарні дроби маємо . Кожен дріб розкладаємо в ряд геометричної прогресії у відповідних областях.

Область |z|<1:

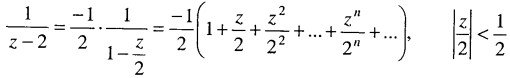
Підставимо ці розклади в і отримаємо рЛ вигляду: , отже , n=0,1,2...; =0, n=1,2,...

18.7 Особливі точки та інтегральні лишки аналітичних функцій

Класифікація ізольованих особливих точок. Особливу точку z0 однозначної аналітичної функції f(z) наз. ізольованою, якщо в її околі 0<|z-z0|<R функція f(z) не має ін. особливих точок.

Особливу точку наз. усувною (правильною), якщо в околі 0<|z-z0|<R точки z0 ряд Лорана функції f(z) має лише правильну частину, тобто

Особливу точку z0 наз. полюсом, порядка m, якщо ряд Лорана для функції f(z) в околі z0 має лише m членів головної частини ряду

m- порядок (кратність) полюса. Якщо m=1, z0-простий полюс.

Особливу точку z0 наз істотно особливою, якщо ряд Лорана має лише головну частину.

Ознака правильної особливої точки: нехай функція f(z) аналітична в околі 0<|z-z0|<R точки z0. Щоб z0 була правильною точкою функції f(z) необхідно і достатньо, щоб існувала скінченна границя .

Ознака полюса: для того, щоб z0 була полюсом m-го порядку аналітичної функції f(z), в околі z=z0, необхідно і достатньо, щоб вона була нулем порядку m функції 1/f(z).

Ознака істотно особливої точки: точка z0 буде істотно особл. точкою аналітичної функції f(z), якщо не існує.

Інтегральним лишком однозначної аналітичної ф-ії f(z) в її ізольованій точці z0 називають коефіцієнт С_-1 при 1/z-z0 у ряді Лорана в околі цієї точки і позначають . Лишок в правильній особливій точці дорівнює нулю.

Лишок для полюса першого порядку в точці а:

Лишок для полюса m-го порядку в точці а:

Приклад 1. Обчисл. лишок функції z+1/z²+4

Знаменник має 2 однократні нулі в точках 2і та -2і,то задана функція має полюси першого порядку в цих точках.Обчислтмо лишки в цих точках:

,

Приклад 2. Знайти лишок функції 1/(z²-1)³.

Функція (z²-1)³=(z-1)³(z+1)³ має в точці z=1 полюс третього порядку, оскільки знаменник має в цій точці трикратний нуль (m=3):