Розділ 17: Перетворення Лапласа та його властивості

17.1. Теоретичні відомості.

Перетворення Лапласа та його властивості є основою операційного числення, азбукою сучасної автоматики та телемеханіки. Вперше їх застосував в електротехнічних розрахунках англійський інженер-електрик О.Хевісайд.

Основна ідея операційного числення: між функцією дійсної змінної f(t) (оригіналом) і функцією комплексної змінної F(p) (зображенням) встановлюється відповідність, яка дозволяє диференціювання та інтегрування оригіналу f(t) зводити до алгебраїчних операцій над зображенням F(p), тобто зводити розв’язок диференціальних, інтегральних, інтегро-диференціальних рівнянь до розв’язання алгебраїчних рівнянь.

Оригінали та зображення

Означення 1. Оригіналами називають функції f(t), які задовольняють умовам:

1) f(t) визначена для усіх t є (-∞,∞), неперервна за виключенням можливо скінченної кількості точок розриву першого роду на кожному скінченному проміжку;

2)f(t) = 0 при t<0 (фізичний процес, який описує f(t), починається в момент часу t=0);

3) існують такі числа М та σ_{0, що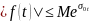} (σ – показник зростання функції f(t)).

Означення 2. Зображенням Лапласа оригіналу називають функцію F(p) комплексної змінної р = σ + і τ, яку визначають за формулою

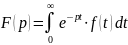
Перетворення Лапласа позначаеться так

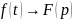
Теорема 1. Для будь-якого оригіналу f(t) зображення F(p) визначено і є аналітичною функуцією в півплощині Re p> σ₀

Одинична функція Хевісайда та її зображення.

Ця функція визначена для усіх t є (-∞,∞), неперервна за винятком точки t=0, обмежена і задовольняє 1-3 умовам означення оригіналу(1), отже є оригіналом.

Знайдемо її зображення Лапласа за формулою (2):

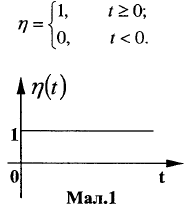
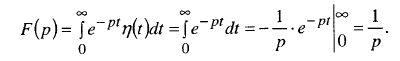
Таким чином: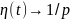

17.2 Властивості зображень Лапласа

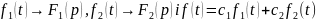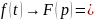
1) Теорема про лінійність. Якщо , де с₁ та с₂ – сталі, то 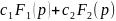, тобто зображення лінійної комбінації оригіналів дорівнює комбінації їх зображень.

2) Теорема зміщення. Якщо 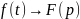і p₀ – довільне комплексне число, то 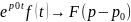для p таких, що Re p> σ₀ + Re p_0, тобто зміщення зображення на p₀ рівносильне множенню оригіналу на

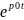
Використовуючи ці властивості, знаходять зображення деяких функцій:

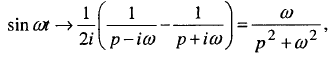
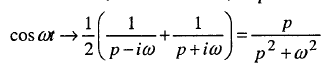
3) Теорема подібності. Якщо 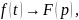то для довільного α>0

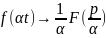
4) Теорема запізнення. Якщо і τ>0 то

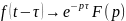
Приклад 1. Знайти зображення функції 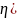τ).

Розв’язання. Оскільки , то за формулою маємо:

τ)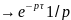

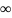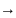5) Теорема про диференціювання оригіналу. Якщо f(t) n раз диференційована на (0, ) і функції f(t), f ^’(t),…,f⁽ⁿ⁾(t) є оригіналами, то із відповідності f(t) F(p) випливає:

f ^’(t) pF(p) – f( +0)

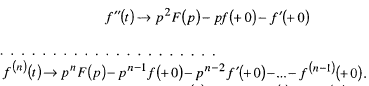
Зауваження 3. Якщо f(0) = 0, то f ^’(t) pF(p).

6) Теорема про диференціювання зображення.

Якщо f(t) F(p), то (-t) f(t) F ^‘(p). (11) тобто диференціювання зображення приводить до множення оригіналу на (-t).

Наслідок. Якщо f(t) F(p), то (-t)ⁿ f(t) F⁽ⁿ⁾_(p).

7) Теорема про інтегрування оригіналу. Якщо f(t) F(p), то

Тобто інтегрування оригіналу в межах від 0 до t відповідає діленню зображення на p.

Означення 3. Згорткою функції f(t) та ϕ(t) називається функція, яка визначається рівністю:

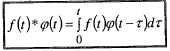
Операція згортання позначається *.

8) Теорема множення зображень. Якщо

Тобто зображення згортки дорівнює добутку зображень функції, що розгортається.