2.3 Анализ устойчивости системы

Устойчивость – это свойство системы возвращаться в исходный или близкий к нему установившийся режим после снятия воздействия, вызвавшего выход из установившегося режима.

Выходная величина устойчивой системы остаётся ограниченной в условиях действия на систему ограниченных по величине воздействий.

Неустойчивая система является неработоспособной, поэтому проверка устойчивости является обязательным этапом анализа системы.

Условием устойчивости линейной системы является отрицательность действительной части корней характеристического уравнения системы. При нулевых корнях система находится на границе устойчивости. Поскольку решение уравнений высокого порядка сопряжено с определёнными трудностями, то анализ устойчивости линейных систем проводится по алгебраическим и частотным критериям. Наиболее часто используют алгебраический критерий Гурвица и частотные критерии Михайлова и Найквиста.

2.3.1 Анализ устойчивости по критерию Гурвица

Критерий Гурвица формулируется следующим образом: для устойчивости линейной системы необходимо и достаточно, чтобы при а₀>0 все диагональные миноры определителя Гурвица были положительными .

Определим устойчивость САР. Для этого можно воспользоваться любой из полученных ранее передаточных функций системы, из которых следует, что характеристическое уравнение системы:

Для устойчивости линейной системы необходимо: положительность всех коэффициентов, при а₀ >0 все диагональные миноры определителя Гурвица были положительными. Так как есть отрицательные коэффициенты, то система неустойчива.

2.3.2 Анализ устойчивости по критерию Михайлова

Этот критерий устойчивости был предложен советским учёным А.В.Михайловым и позволяет судить об устойчивости замкнутой системы на основании рассмотрения некоторой кривой.

Формулировка критерия Михайлова сводится к следующему: чтобы замкнутая система автоматического управления была устойчива, необходимо и достаточно, чтобы кривая Михайлова при изменении частоты от 0 до , начинаясь при на вещественно положительной полуоси, обходила только против часовой стрелки последовательно n квадрантов, уходя в бесконечность в последнем квадранте, где n – порядок характеристического уравнения.

Определим устойчивость САР:

В характеристическом уравнении для замкнутой системы вместо оператора р подставим значение (jw) и получим:

_где

Выделим вещественную и мнимую части.

,

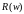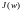Давая различные значения частоте ω, находим координаты и точек годографа Михайлова. Полученные данные заносим в таблицу 1 и строим по ним годограф (рисунок 9).

Таблица 1 —Значения координат и точек годографа Михайлова

	0	0,2	0,4	1	1,2	2	∞
	-3	-7,12	-51,7	-287	-396	-851	-∞
	0	1,89	41,4	-36	-130	-1,1·103	-∞

Рисунок 9 — Годограф Михайлова

Вывод: Годограф Михайлова не начинается на вещественно положительной полуоси и при изменении w от 0 до ∞ не проходит против часовой стрелки 4 квадранта, где 4 – порядок характеристического уравнения системы. Таким образом система является неустойчивой.

2.3.3 Анализ устойчивости по критерию Найквиста

Критерий устойчивости Найквиста основан на использовании амплитудно-фазовой частотной характеристики (АФЧХ) разомкнутой системы.

Строится график АФЧХ в координатах и . Для этого рассчитываются и при изменении частоты от 0 до . Длина вектора, соединяющего начало координат с графиком АФЧХ, равна значению при частоте , а угол поворота от оси R равен .

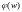Если система в разомкнутом состоянии устойчива, то для устойчивости замкнутой системы необходимо и достаточно, чтобы АФЧХ разомкнутой системы при изменении частоты от нуля до бесконечности не охватывала точку с координатами (-1,j0).

Если система в разомкнутом состоянии находится на границе устойчивости (является астатической), то для устойчивости замкнутой системы необходимо и достаточно, чтобы АФЧХ разомкнутой системы, дополненная дугой бесконечно большого радиуса против часовой стрелки до действительной полуоси, не охватывала точку с координатами (-1,j0).

Если система в разомкнутом состоянии неустойчива, то для устойчивости в замкнутом состоянии необходимо и достаточно, чтобы АФЧХ разомкнутой системы охватывала точку с координатами (-1,j0) в положительном направлении к/2 раз, где к – число корней характеристического уравнения с положительной действительной частью.

Определим устойчивость САР для нашего случая.

Передаточная функция разомкнутой системы по задающему воздействию имеет вид:

Находим частотную передаточную функцию, подставляя 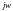вместо :

Так как и т.д., получим:

.

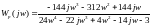Для построения АФЧХ разомкнутой системы представим частотную передаточную функцию в виде:

Чтобы представить частотную передаточную функцию в виде комплексного числа имеющего действительную и мнимую части, умножим и разделим полученный результат на сопряжённое знаменателю комплексное число 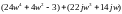и после преобразования получим:

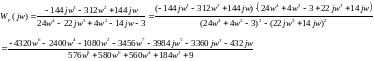
Вещественная часть частотной передаточной функции:

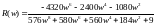
Мнимая часть частотной передаточной функции:

.

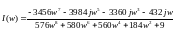Найдём координаты точек, которые являются местом пересечения годографа с осью ординат. Для этих точек координата по оси абсцисс равна нулю ( =0). То есть годограф пересекает ось , если числитель равен нулю, а именно:

Найдём координаты точек, которые являются местом пересечения годографа с осью ординат. Для этих точек координата по оси ординат равна нулю ( =0). То есть годограф пересекает ось , если числитель равен нулю, а именно:

.

_{Таблица 2 ― Значения координат} и

	0	0,2	0,6	1	1,8	∞
	0	-2,7	-4,9	-4,1	-1,9	-∞
	0	24,7	42,1	-36	-734	­-∞

Рисунок 10 ― АФЧХ разомкнутой системы

Вывод: АФЧХ разомкнутой системы при изменении частоты w от 0 до ∞ охватывает точку с координатами (–1,j0), поэтому замкнутая система является неустойчивой.

2.4 Оценка качества управления

Устойчивость САУ или САР является необходимым, но ещё не достаточным условием практической полезности системы. К системе должен быть предъявлен ещё целый комплекс требований, который объединяется понятием качества процесса управления. Оценка качества САУ ведётся по так называемым показателям качества, к которым относятся:

1) точность системы в установившемся состоянии;

2) качество переходного процесса (или показатели качества переходной характеристики).

Любая система независимо от своего назначения и конструкции должна осуществлять управление каким-либо объектом с определённой точностью, т.е. качество управления зависит от мгновенных (переходных) величин ошибки , равных разности между заданными g(t) и фактическими y(t) значениями управляемой величины.

= g(t)- y(t).

Возмущающие воздействия представляют собой случайные функции времени, поэтому оценка качества по мгновенным значениям ошибки практически не используется.

Одной из оценок качества регулирования служит оценка качества переходной характеристики САУ относительно задающего воздействия. Показатели качества переходной характеристики называются прямыми. Чем лучше переходная характеристика, тем лучше система будет отрабатывать произвольно задающее воздействие.

Качество САУ по переходной характеристике оценивается обычно по следующим показателям: Величине перерегулирования h; статической ошибке , времени переходного процесса t_p; числу колебаний с (колебательность), степени затухания .

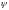Заносим данные в таблицу 3 и строим переходную характеристику (рисунок 11)

Таблица 3 ― Значения переходной характеристики

Время,мин	0	2	4	6	8	10	12	14	16	18	20	22	24	26	28	30	32
Темпер.,°С	15	20	27	35	42	50	59	65	74	80	85	92	90	90	88	86	81
Время,мин	34	36	38	40	42	44	46	48	50	52	54	56	58	60	62	64
Темпер.,°С	84	86	91	90	88	46	46	84	84	86	88	88	86	86	84	86

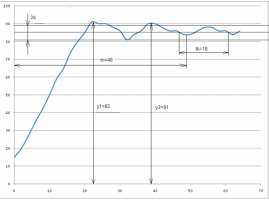
Рисунок 11 ― Переходная характеристика САУ

Величина перерегулирования определяется по выражению:

,

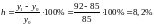где y₁- амплитуда первого отклонения;

y₀- значение задания.

Перерегулированием оценивают разность между максимальным значением y_1, переходной характеристики и значением задания у₀. Перерегулирование косвенно определяет также запас устойчивости. Допустимое значение перерегулирования может быть установлено на основании опыта эксплуатации подобных систем. В большинстве случаев считается, что запас устойчивости является достаточным, если величина перерегулирования не превышает 10…30%.

Время переходного процесса t_p характеризует быстродействие системы, под которым понимается промежуток времени от начала приложения воздействия до вхождения y(t) в коридор , где - допустимая динамическая погрешность. Обычно принимают =0,01…0,05 иногда до 0,2, т.е. переходной процесс в САУ считают закончившимся, когда y(t) отличается от своего установившегося значения не более чем на 1…5%. Обычно выбирают равным 5%.

Период колебаний – время между двумя максимумами – T_к:

Т_к =18 мин

Колебательность или число колебаний за время переходного процесса определяется числом максимумов или числом минимумов за время t_n=48мин.

Обычно с=1…2 колебания, иногда 3…4. У некоторых систем колебания вовсе не допускаются. Если 1 , то запас устойчивости САУ считается достаточным.

Собственная частота колебаний системы: