После преобразований получим исходные дифференциальные уравнения для определения и :

(3.31)

где – электромеханическая постоянная времени привода, с;

– ток короткого замыкания, соответствующий новой электромеханической характеристике 2, рис. 3.9, на которой будет работать двигатель после окончания переходного процесса в генераторе, А;

– ток короткого замыкания, соответствующий прежней электромеханической характеристике 1, на которой работал двигатель до начала переходного процесса в генераторе, А;

– частота вращения идеального холостого хода двигателя новой характеристики 2, соответствующая , ;

– частота вращения холостого хода двигателя прежней характеристики 1, соответствующая , .

– частота вращения двигателя при , .

Решив исходные дифференциальные уравнения, получим:

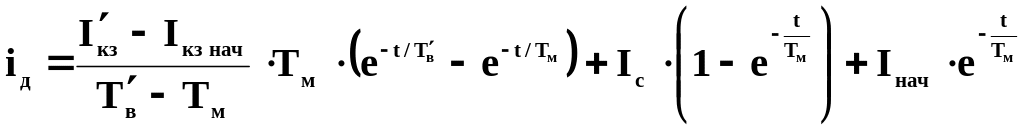, (3.32)

, (3.33)

, (3.34)

где – ток двигателя при , А;

– ток двигателя до начала переходного процесса, ;

– частота вращения двигателя до начала переходного процесса, с^-1 .

Для участка , , , .

Для участка , где происходит снижение скорости тележки до ползучей, , , так как отключается напряжение обмотки возбуждения и она оказывается закороченной на резистор , что соответствует переходу с исходной характеристики 1, рис. 3.10, на новую характеристику 2, проходящую через начало координат с и . и соответствуют току короткого замыкания и частоте вращения холостого хода исходной характеристики 1, на которой обеспечивается движение тележки с . , , а вместо записывается . При снижении тока возбуждения до величины и соответственно ЭДС генератора до на схему обмотки возбуждения генератора снова подается напряжение, равное . На этом заканчивается рассматриваемый этап, длительность которого определяется по формуле (3.25).

На участке в обмотке возбуждения генератора переходного процесса нет и, следовательно, двигатель работает на характеристике, обеспечивающей движение тележки с , поэтому , . и равны соответствующим значениям величин в конце предыдущего участка.

На участке , после отключения питания обмотки возбуждения генератора, изменения тока и частоты вращения (до остановки двигателя) описываются теми же уравнениями, что и на участке т.е. , . При этом и соответствуют току короткого замыкания и частоте вращения холостого хода исходной характеристики, где обеспечивалось движение тележки с : , , . В момент времени двигатель останавливается, а ЭДС генератора . Время торможения двигателя определяется из (3.23), где второе слагаемое приравнивается к , а :

. (3.35)

На участке , после остановки двигателя:

(3.36)

где – ЭДС генератора в момент остановки двигателя, В.

(3.37)

Кривая динамической механической характеристики строится по переходным кривым и . При проводят вертикаль до пересечения с кривыми и и определяют координаты точек и , которые наносят в плоскости . Затем берется следующее и через его конец проводят вертикаль. Точки пересечения вертикали с кривыми и определяют координаты следующей точки и для плоскости и т.д.

3.2.2. Расчет и построение переходных процессов

Системы г – д со схемой возбуждения рис. 3.6, а

Как и в предыдущем случае, после подачи напряжения на схему возбуждения генератора ток обмотки возбуждения начинает увеличиваться, изменяясь также по экспоненциальному закону:

. (3.38)

При достижении тока возбуждения величины I_вн происходит расшунтирование резистора R2. Время нарастания тока возбуждения до I_вн определяется из выражения (3.38):

. (3.39)

По аналогии с выражением (3.38) запишется и уравнение ЭДС генератора:

(3.40)

Уравнение (3.40) позволяет описать изменение ЭДС генератора на всех участках движения тележки, рис.3.11. На участке используется первое слагаемое, так как процесс начинается с момента подачи напряжения на схему возбуждения генератора и . определяется из выражения (3.24). В момент времени ЭДС генератора достигает величины , которая обеспечивает вращение двигателя в установившемся режиме с , и резистор расшунтируется. На интервале ЭДС генератора остается неизменной, равной .

В момент времени ЭДС генератора достигнет такой величины, что обеспечит протекание тока и , после чего двигатель начнет вращаться. В соответствии с выражением (3.24) . Тогда продолжительность интервала с учетом (3.40) определится из выражения:

. (3.41)

Переход на ползучую скорость и последующая остановка тележки осуществляется аналогично предыдущей схеме включения обмотки возбуждения генератора.

Необходимо отметить, что на каждом очередном участке, описываемом соответствующим уравнением, отсчет текущего значения времени начинается с нуля.

Переходные процессы , и приведены на рис. 3.11 и рассматриваются аналогично предыдущему варианту схемы возбуждения генератора. Ниже приводятся зависимости, без учета постоянной времени якорной цепи .

На первом участке , когда двигатель неподвижен, уравнение равновесия ЭДС и напряжений якорной цепи системы Г-Д с учетом выражения (3.40) будет иметь вид:

. (3.42)

Тогда

, (3.43)

, (3.44)

где – ток короткого замыкания, соответствующий новой электромеханической характеристике I, рис.3.9, на которой будет работать двигатель после окончания переходного процесса в генераторе. Продолжительность первого участка определяется из выражения (3.41).

Для второго и последующих участков уравнение равновесия ЭДС и напряжений записывается как и для уравнения (3.30), после преобразования которого, получим исходные дифференциальные уравнения для определения зависимостей , , , аналогичные предыдущей схеме, где , . В уравнениях (3.32) и (3.33) необходимо провести те же замены, т.е. , , .

На участке в момент времени происходит расшунтирование резистора и ЭДС генератора становится неизменной, и равной , но величины и не достигнут еще своих установившихся значений и переходный процесс будет продолжаться еще некоторое время. Зависимости и описываются уравнениями (3.32) и (3.33), где первые слагаемые равны нулю, так как и , а и равны соответствующим их значениям в конце предыдущего участка.

На оставшихся участках все процессы рассматриваются точно также как и для схемы рис.3.5,а.