43)Теплопроводность плоской стенки.

Р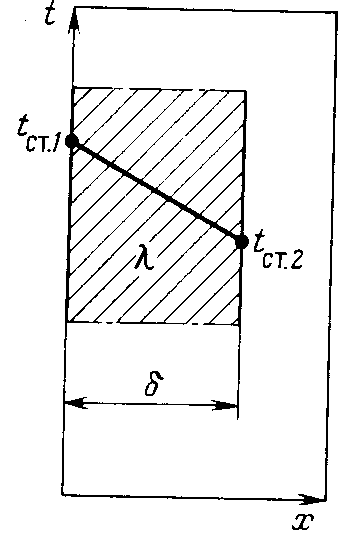 ассмотрим передачу тепла теплопроводностью через плоскую стенку, длина и ширина которой больше её толщины. Температуры наружных поверхностей стенки равны t₁ и t₂. При установившемся процессе количество тепла, подведенного к стенке и отведенного от неё должны быть равны между собой и не должны изменяться во времени. Предположим, что удельная теплопроводность, теплоемкость и плотность не изменяются, при чем температура изменяется только в направлении оси x, т.е. температурное поле одномерно. . Тогда на основании уравнения теплопроводности имеем: (1), С₁ и С₂ – константы интегрирования. Уравнение (1) показывает, что по толщине плоской стенки температура изменяется по линейному закону. Константы интегрирования определяют исходя из следующих граничных условий: x=0 при t=t_ст1  t_ст1=С₂, x= при t=t_ст2  t_ст2=С₁+С₂.

. Подставив полученное выражение температурного градиента в уравнение теплопроводности и определим количество переданного тепла: .

- уравнение теплопроводности плоской стенки. .

44)Теплопроводность многослойной стенки.

Е сли плоская стенка состоит из слоев, отличающихся друг от друга теплопроводностью и толщиной, то при установившемся процессе через каждый слой стенки пойдёт одно и то же количество тепла, которое может быть выражено для различных слоев уравнениями:

1слоя: ,

2слоя: ,

3слоя: ,

n слоя: .

45)Конвективный теплообмен. Законы Ньютона.

Решение задачи о количестве тепла, передаваемого от стенки к среде или от среды к стенке связано с необходимостью знать температурный градиент у стенки и профиль изменения температур теплоносителя вдоль поверхности теплообмена, определение которых затруднительно. Поэтому для удобства расчета теплоотдачи в основы его кладут уравнение, известное под названием закона теплоотдачи или закона Ньютона . Он гласит, что количество переданного тепла от стенки к жидкости или наоборот пропорционально поверхности теплообмена, времени и разности температур между стенками и жидкостью. Коэффициент пропорциональности  называется коэффициентом теплоотдачи и характеризует интенсивность переноса тепла между поверхностью тела, например, твердость стенки и окруж. среды.

. Коэффициент теплоотдачи показывает, какое количество тепла передается от стенки к среде или наоборот через единицу поверхности в единицу времени при разности температур между стенкой и жидкостью равной 1⁰С.

46)Дифференциальное уравнение конвективного теплообмена.

В ыделим установившемся потоке жидкости элементарный параллелепипед с ребрами dx, dy, dz. Пусть плотность жидкости, её коэффициент теплопроводности и уд. Теплоемкость постоянны. Температура жидкости изменяется вдоль грани параллелепипеда. Проекции скорости движения жидкости W на оси координат (x; y; z) составляют W_x; W_y; W_z. Вдоль оси x, т.е. через грань dydz за время d в параллелепипед поступает путём конвекции следующее количество тепла: . Количество тепла, удаляющего путём конвекции за то же время через противоположную грань параллелепипеда составит:

.

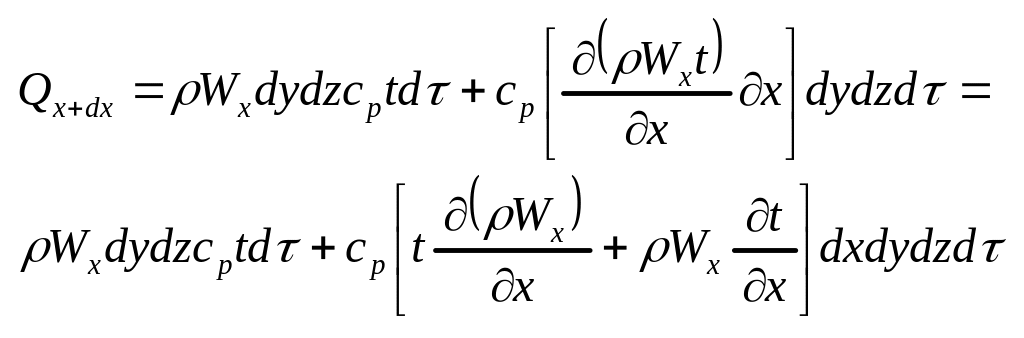Тогда разность между количеством поступающего в параллелепипед и удаляющего из него тепла за время d в направление оси x составит:

. Проведя аналогичные расчеты в отношении других осей, получим:

Общее количество тепла, подведенного конвекцией в параллелепипед за время d составит:

Согласно дифференциальному уравнению неразрывности потока при =const выражение, стоящее в квадратных скобках равно нулю. (divW=0). Произведение dxdydz=dV. Следовательно, конвективная составляющая теплового потока примет вид:

. Количество тепла, вносимое в параллелепипед за время путём теплопроводности составит:

Это количество тепла равно соответствующей изменению энтальпии параллелепипеда . Таким образом получим следующее выражение:

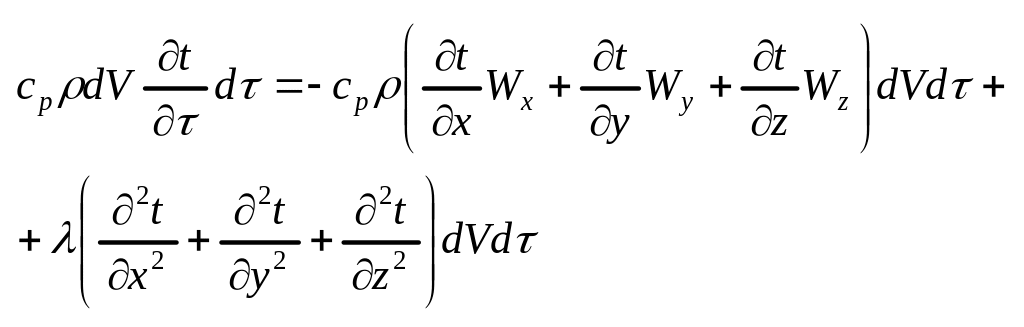
- Диф. уравнение Фурье – Кирхгофа, оно выражает в наиболее общем виде распределение температур в движущейся жидкости.