40)Температурное поле и температурный градиент.
К числу основных задач теорий теплообмена относится установление зависимости между тепловым потоком и распределением температур в средах. Совокупность мгновенных значений любой величины во всех точках данной среды, называется полем данной величины; соответственно совокупность значений температур в данный момент времени для всех точек рассматриваемой среды, называется температурным полем. В наиболее общем случае температура поля зависит от координат точки (x; y; z) и изменяется во времени функцией t=f(x; y; z; ). В отличие от температуры, которая явл. скалярной, тепловой поток связанный с направлением переноса тепла представляет собой векторную величину.
П
усть
разность температур между двумя
ближайшими изотермами составляет t,
составляет кратчайшее расстояние между
погрешностями n.
При движении этих поверхностей отношение
t/n
стремится к пределу
.
Произвольная температура по нормали
изотермической поверхности, называется
температурным градиентом. Этот градиент
явл. вектором, направление которого
соответствует повышению температуры.
Значение температурного градиента
определяет наибольшую скорость изменения
температур в данной точке температурного
поля.
41)Передача тепла теплопроводностью. Закон Фурье.
Основным законом передачи тепла теплопроводностью явл. закон Фурье, согласно которому количество тепла dQ, передаваемое посредством теплопроводности через элемент поверхности dF перпендикулярно тепловому потоку поверхности dt/dn и времени d:
.
Знак «-» показывает на то, что тепло
перемещается в сторону падения температур.
Коэффициент пропорциональности
называется коэффициентом теплопроводности
.
Коэффициент теплопроводности показывает
какое количество тепла походит вследствие
теплопроводности в единицу времени
через единицу поверхности теплообмена
при падении температуры на 1 градус и
на единицу длины нормали к изотермической
поверхности. Коэффициент теплопроводности
характеризует способность тела проводить
тепло путём теплопроводности. При
обычных температурах и давлениях лучшими
проводниками явл. Ме., а худшими явл.
газы.
42)Дифференциальное уравнение теплопроводности.
В
ыделим
водородное и изотропное тело, объёмом
dV
dxdydz.
Физические свойства тела, такие как
плотность, теплоемкость и теплопроводность
одинаковы во всех точках параллелепипеда
и не изменяются во времени. Температура
на левой грани равна t,
на противоположной
.
Количество
тепла, входящего в параллелепипед через
его грани за промежуток времени d,
определим следующим образом:
по оси х
через
грань dydz:
,
по оси y
через
грань dxdz:
,
по оси z
через
грань dxdy:
.Количество
тепла, выходящего из параллелепипеда
через противоположные грани за тот же
помежуток времени: по оси х:
,
по оси y:
,
по оси z:
.
Количество
тепла, входящего через соответствующую
грань параллелепипеда не равна количеству
тепла, выходящему через противоположную
грань, т.к. часть тепла расходуется на
повышение температуры в объёме
параллелепипеда. Разность между
количеством, вошедшим в параллелепипед
и вышедшим из него тепла за время d
составит: по оси x:
по
оси y:
по оси z:
.
Полное превращение тепла параллелепипеда
за промежуток времени
.
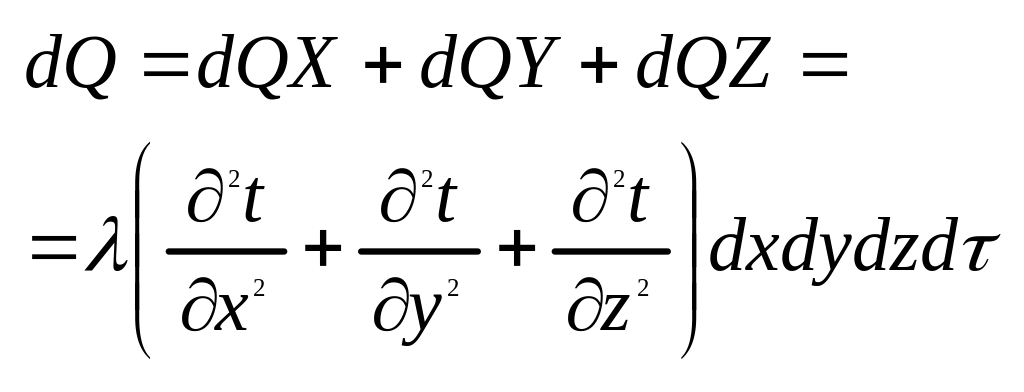Выражение в круглых скобках носит
название оператора Лапласа и учитывая
dxdydz=dV,
получим следующее выражение:
(1).
По закону сохранения энергии превращение
количества тепла в параллелепипеде
равно изменению энтальпии параллелепипеда:
(2).
Приравняем (1) и (2):
,
,
(3)-уравнение
теплопроводности в дифференциальной
форме. Уравнение (3) определяет температуру
в любой точке тела, через которое тепло
передается теплопроводности. а
– коэффициент температуроповодности.
.
Коэффициент температуроповодности
характеризует тепло инерционные свойства
тела, т.е. при прочих равных условиях
быстрее нагреется или охладится то
тело, которое обладает большим
коэффициентом а.