I I. Построение:
1)
2) А1, С1 | А1,С1
3) С1АН | С1АН= А
4) АС1К | АС1К= С
5) В1 | В1=[AH) [CK)
6) M1 | B1M1=M1C1
7) [AM1]
8) [AМ] | [AМ] [AM1)
9) В | B
[AH),
,
где 
10)C | C
[AC1),
,
где
11) АВС – искомый.
III. Док-во:
По построению АВС подобен АВ1С1. Отсюда вытекает, что АМ – медиана АВС (т.к. АМ1- медиана АВ1С1); С –равен данному углу(т.к. по построению С1= С). Следовательно, АВС - искомый.
IV. Исследование:
Т.к. точки А и С1 выбраны произвольно, то существует бесконечно много треугольников, удовлетворяющих двум данным углам. Но все эти треугольники будут подобны друг другу. Учитывая что пункт 8 выполняется однозначно, то такой треугольник будет единственным.
Метод решения задачи:
В данной задачи целесообразно в качестве метода решения выбрать метод подобия, с использование гомотетии с центром в точке А и коэффициентом k.
Возможны затруднения:
1) при выборе метода построения
2) При использовании гомотетии в построении (выбор коэффициента гомотетии)
3) при доказательстве единственности решений.
63. Решить задачу на построение.
Дано: Р(2,2); а=(ОХ), b|
(8,1)
,
(3,10)
Построить: АВP | AB=BP=AP, А= B= P
I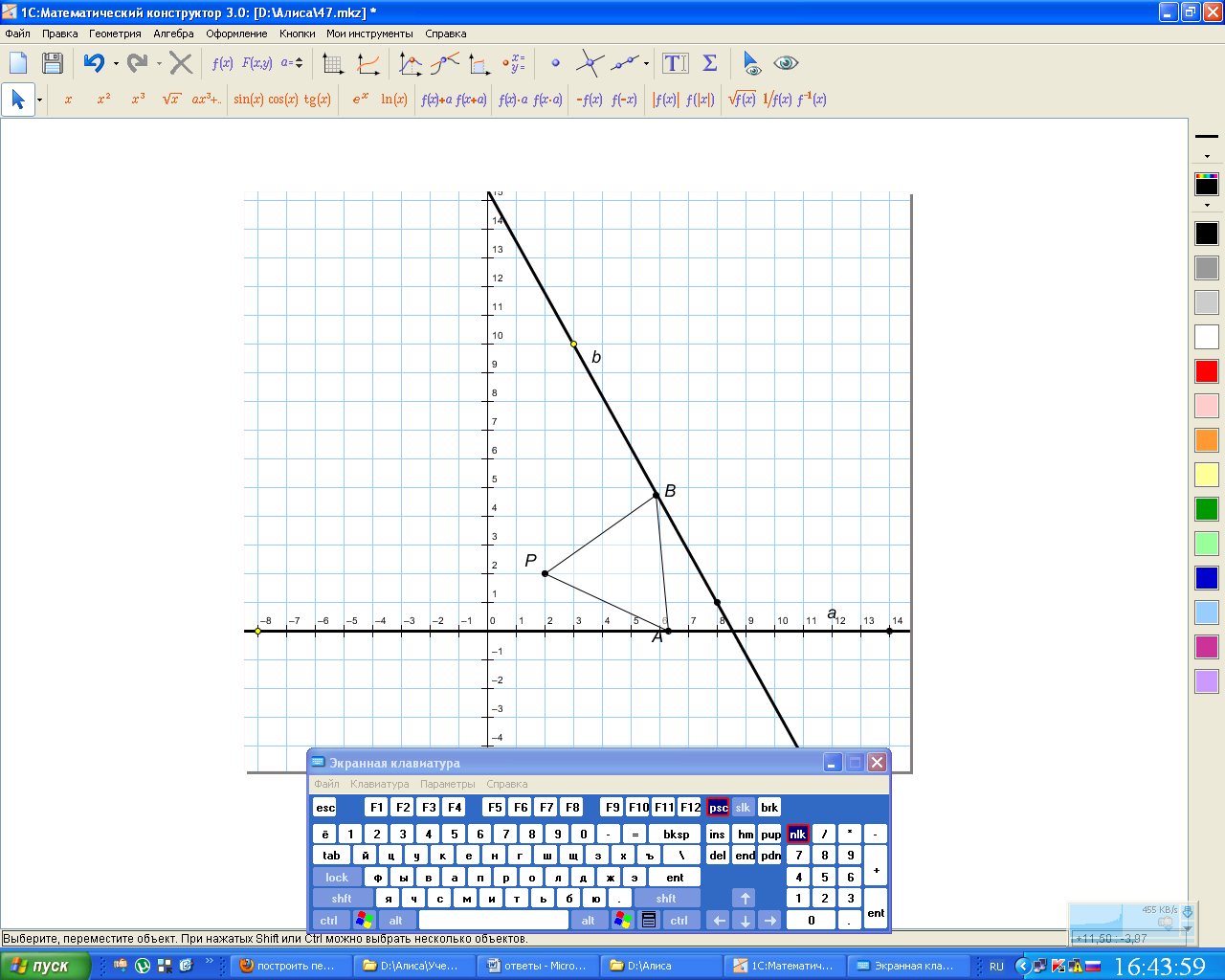
.
Анализ: пусть
АВР
искомый. А
,
B
.
Т.к. треугольник правильный, то можно
воспользоваться поворотом на 60º вокруг
точки Р. Сначала построим прямую b1
– являющейся поворотом прямой b.
Точка пересечения прямой b1
и а будет являться точкой А. Повернув
точку А вокруг точки Р на -60º получим
точку В, которая будет лежат на прямой
b.
II. Построение:
1) P, a, b | Р(2,2); а=(ОХ), b| (8,1) , (3,10)
2) PH | PH b, H (//построение : из точки Т(3,10) проводим дугу, радиусом ТР и из точки И(8,1) проводим дугу радиусом ИР. Точки пересечения этих дуг соединяем и получаем точку Н)
3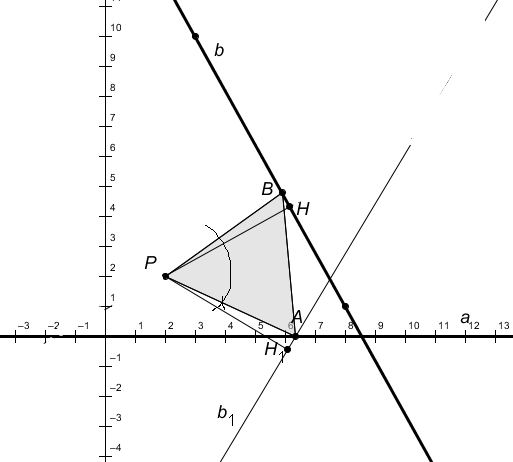
)
H1| 
(//60º-это провести дугу и отложить радиус
этой дуги от прямой)
4) PH1
5) b1 | PH1 b1, H1 b1
6) A | A=b1 a
7) B | 
8) АВP – искомый
III. Док-во:
По построению: точка А
,
РВА=60º.
Т.к. точка А
b1
( по построению), то 
принадлежит b.
Следовательно
АВР
– искомый.
IV. Исследование:
Задача имеет единственное решение, т.к все пункты построения выполняются однозначно
Метод решения задачи:
В данной задачи целесообразно в качестве метода решения выбрать метод поворота с центром в точке Р на 60º
Возможны затруднения:
1) при выборе метода построения
2) При использовании поворота в построении
3) при доказательстве единственности решений.
46.
I. составление математической модели.
1) оптимизируемая величина y=Sбок , поскольку в задаче требуется выяснить когда Sбок будет наибольшим.
2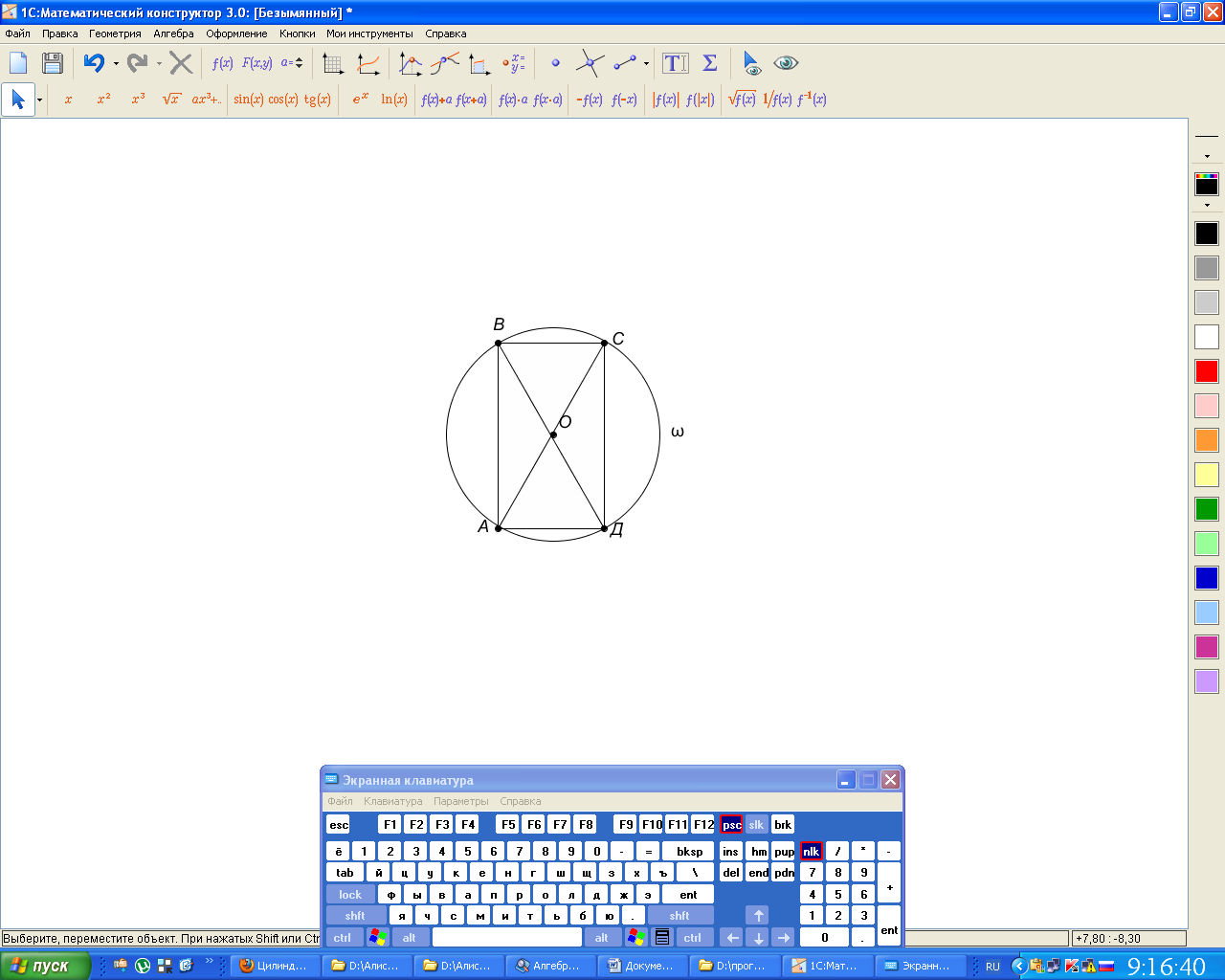
)
Независимая переменная х:
Рассм осевой
сечение комбинации этих тел. Получим
окружность, в которой вписан прямоугольник
АВСД, центр окр-ти О – середина диагоналей
АС и ВД. Следовательно, АС=ВД=2R,
АД=2rц,
Hц=СД=
.
Поэтому за значение независимой
переменной х возьмем радиус цилиндра.
Т. к. АВСД вписан в окр-ть, то 
.
3) y=Sбок=
Вычислим высоту
цилиндра через радиус. Hц=СД=
=
Получаем 
.
Математическая модель задачи составлена.
II. работа с составленной моделью.
Для функции 
,
надо найти унаиб.
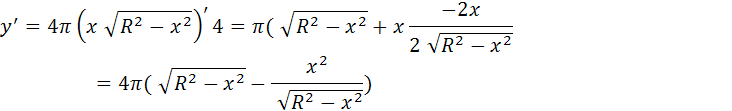
Приравняем производную нулю, получим
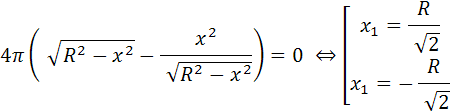
Заданному отрезка принадлежит лишь точка х=х1.
Вычислим значение функции в точке х, и на концах отрезка.
,
,
. Следовательно унаиб=
III. Ответ на вопрос задачи
В задаче спрашивается объем цилиндра.
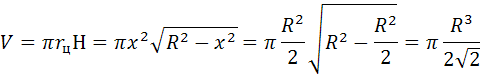
Ответ: 
I. составление математической модели.
1) оптимизируемая величина y=Sбок+Sосн, поскольку в задаче требуется выяснить когда Sбок+Sосн будет минимальным..
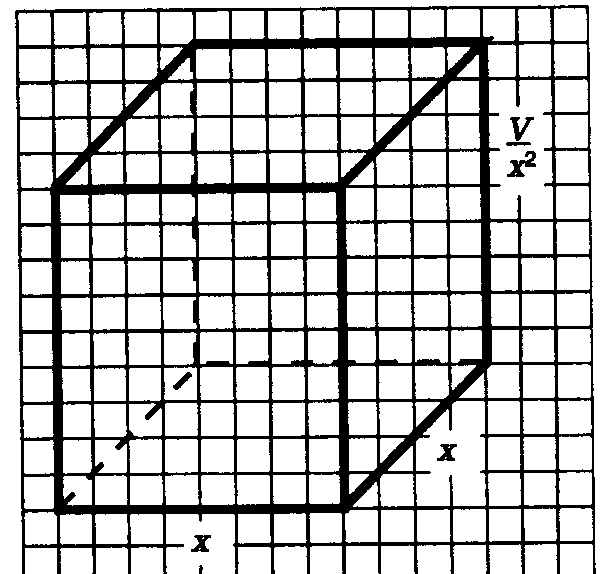
3) если h
– высота бассейна, то V=x2h,
откуда находим 
Поверхность
бассейна состоит из квадрата со стороной
х и четырех прямоугольников со сторонами
х и 
. Значит,
III. Ответ на вопрос задачи
В задаче спрашивается Sбок
Ответ:
