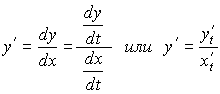Свойства дифференциала.

В этом и следующем параграфах каждую из функций будем считать дифференцируемой при всех рассматриваемых значениях её аргументов.

Дифференциал обладает свойствами, аналогичными свойствам производной:

 (С – постоянная величина)  (8)

                                (9)                              (10)

                                      (11)

                            (12)

Производные и дифференциалы высших порядков

Производные высших порядков.

Рассмотрим функцию   , определенную на некотором промежутке    . Вычислим производную  , которая также является функцией на  . Производной второго порядка от функции   называется производная от ее производной:    . Аналогично определяют производную любого порядка:   .

Дифференциалы высших порядков.

Рассмотрим дифференциал функции   в произвольной точке промежутка  :  . Здесь   - приращение независимой переменной, которое является числом и не зависит от  . Сам же дифференциал есть функция от  , и можно вычислить дифференциал от этой функции:    При   этот дифференциал от дифференциала называется дифференциалом второго порядка и вычисляется по формуле  Аналогично вычисляется дифференциал любого порядка  .

Дифференцирование функций, заданных параметрически

До сих пор функция записывалась в явном виде y= f(x) и в неявном F(x,y)=0. Но существует еще третий вид аналитического представления функции - это представление её в па раметрической форме в виде двух уравнений

где t - вспомогательная переменная, называемая параметром.   Заметим, что функция может быть представлена в параметрической форме различными способами.   Например, функция, записанная в неявном виде x² + y² = 1 может быть представлена в явном виде:   и в параметрической форм е:

  Заметим, что x² + y² = 1 есть уравнение окружности единичного радиуса с центром в начале координат.   В первом параметрическом представлении уравнения x² + y² = 1 параметр t изменяется от -1 до +1 и равен абциссе подвижной точки окружности, во втором случае параметр t изменяется от 0 до 2p и равен углу, образованному радиусом подвижной точки и осью Ox.   Если функция задана в явном виде y=f(x), то всегда можно записать её в неявном виде y-f(x)=0, а также в параметрической форме

От вида F(x,y)=0 не всегда возможно перейти к виду y=f(x) или x=j (y), так как уравнение F(x,y)=0 может оказаться неразреш имым относительно y или x .   Лего перейти от параметрического представления функции к уравнению вида y=f(x). Для этого из первого уравнения x=x(t) нужно найтиt=t(x), если конечно это возможно , и подставить его во второе уравнение y=y(t)

y=y[t(x)]=f(x)

   От параметрического представления функции к уравнению вида F(x,y)=0 можно прийти путем исключения параметра t, если это возможно.    Уравнения y=f(x) и F(x, y)=0 служат различными аналитическими представлениями одной и той же функции F[x, f(x)]=0. Параметрические уравнения

и уравнение F(x, y)=0 представляют одну и ту же функцию, если F(x(t), y(t))=0.    Наконец, параметрические уравнения определяют ту же функцию, что и уравнение y=f(x), если

y(t)=f [ x(t) ].

   Найдем производную функции y по x в случае, когда она задана в параметрическом виде. Для этого будем рассматривать t как функцию от x. То есть t=t(x). Тогда y=y[t(x)]. Продифференцируем y как сложную функцию от x, т.е. по формуле

и применим формулу, связывающую производные обратных функций:

   Введя обозначения ,        получим