
- •Явное и неявное задание функции (декартовая и полярная система координат)
- •Предел последовательности действительных чисел (определения последовательности)
- •Односторонние пределы функций
- •Производная функции в точке. Односторонние производные (определения)
- •Основные правила дифференцирования (±, (uv)’, (u/V)’)
- •Отсюда видно, что искомая производная равна
- •Свойства дифференциала.
- •Производные и дифференциалы высших порядков
- •Дифференцирование функций, заданных параметрически
- •Дифференцирование функций, заданных неявно
- •Теорема Лагранжа
- •Теорема Коши
- •Необходимое условие экстремума дифференцируемой функции. Достаточные условия существования экстремума (по первой производной)
- •Достаточные условия существования экстремума функции через производные высших порядков Достаточное условие экстремума
- •Выпуклость и вогнутость. Определения. Необходимое и достаточные условия выпуклости и вогнутости функции
- •Интегрирование рациональных дробей
Производная функции в точке. Односторонние производные (определения)
Определяются
также односторонние производные, где
вместо соответствующего предела
используется односторонний
(левосторонний и правосторонний)
предел. Правосторонняя
производная или
производной
справа обозначается
символами ![]() . Левосторонняя
производная или производная
слева обозначается
символами
. Левосторонняя
производная или производная
слева обозначается
символами ![]() .
Обычная производная существует тогда
и только тогда, когда существуют равные
между собой односторонние производные
(их величина и равна производной).
.
Обычная производная существует тогда
и только тогда, когда существуют равные
между собой односторонние производные
(их величина и равна производной).
Односторонний предел по Гейне
Число
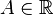 называется правосторонним
пределом (правым
пределом, пределом
справа) функции
в
точке
,
если для всякой последовательности
называется правосторонним
пределом (правым
пределом, пределом
справа) функции
в
точке
,
если для всякой последовательности 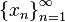 ,
состоящей из точек, больших числа
,
которая сама сходится к числу
,
соответствующая последовательность
значений функции
,
состоящей из точек, больших числа
,
которая сама сходится к числу
,
соответствующая последовательность
значений функции 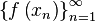 сходится
к числу
сходится
к числу 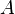 .
.
![]()
Число называется левосторонним пределом (левым пределом, пределом слева) функции в точке , если для всякой последовательности , состоящей из точек, меньших числа , которая сама сходится к числу , соответствующая последовательность значений функции сходится к числу .[1]
![]()
Односторонний предел по Коши
Число
называется правосторонним
пределом (правым
пределом, пределом
справа) функции
в
точке
,
если для всякого положительного
числа ![]() отыщется
отвечающее ему положительное число
отыщется
отвечающее ему положительное число ![]() такое,
что для всех
точек
такое,
что для всех
точек ![]() из интервала
из интервала ![]() справедливо неравенство
справедливо неравенство ![]() .
.
![]()
Число
называется левосторонним
пределом (левым
пределом, пределом
слева) функции
в
точке
,
если для всякого положительного
числа
отыщется
отвечающее ему положительное число
,
такое, что для всех точек
из
интервала ![]() справедливо
неравенство
.[1]
справедливо
неравенство
.[1]
![]()
Геометрический, механический смысл производной
Геометрический - Производная в точке x0 равна угловому коэффициенту касательной к графику функции y=f(x) в этой точке
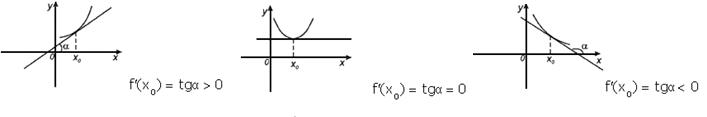
Физический смысл производной - Если точка движется вдоль оси х и ее координата изменяется по закону x(t), то мгновенная скорость точки:
![]()
Необходимое условие существования производной
Если функция имеет в определенной точке производную, то существует касательная к графику этой функции в этой точке, причем угловой коэффициент этой касательной равен значению производной.
Теорема
(необходимое условие существования
производной функции в точке). Если
функция y = f(x) имеет производную в
точке![]() ,
то функция f(x) в этой точке непрерывна.
,
то функция f(x) в этой точке непрерывна.
Доказательство
Пусть
существует ![]() .
Тогда
.
Тогда
![]() ,
где
,
где
![]() –
бесконечно малая при
–
бесконечно малая при ![]() .
⇒
.
⇒ ![]() ;
;
⇒
.
Но это означает, что функция f(x) непрерывна в точке (по геометрическому определению непрерывности).
Замечание. Непрерывность функции в точке не является достаточным условием существования производной этой функции в точке . Например, функция y = |x| непрерывна, но не имеет производной в точке .
Очевидно,
что соответствие![]() является
функцией, определенной на некотором
множестве
является
функцией, определенной на некотором
множестве![]() .
Ее называют производной
функции y
= f(x) и обозначают
.
Ее называют производной
функции y
= f(x) и обозначают
![]() .
.
Операцию нахождения для функции f(x) ее производной функции называют дифференцированием функции y = f(x).
