Явное и неявное задание функции (декартовая и полярная система координат)

Если функция задана уравнением у=ƒ(х), разрешенным относительно у, то функция задана в явном виде (явная функция). Под неявным заданием функции понимают задание функции в виде уравнения F(x;y)=0, не разрешенного относительно у. Всякую явно заданную функцию у=ƒ (х) можно записать как неявно заданную уравнением ƒ(х)-у=0, но не наоборот.

Полярная система координат — двухмерная система координат, в которой каждая точка на плоскости определяется двумя числами — полярным углом и полярным радиусом. Полярная система координат особенно полезна в случаях, когда отношения между точками проще изобразить в виде радиусов и углов. Если в качестве координатных осей берутся прямые, перпендикулярные друг другу, то система координат называется прямоугольной. Прямоугольная система координат, в которой единицы измерения по всем осям равны друг другу, называется декартовой системой координат.

Параметрическое представление — используемая в математическом анализе разновидность представления переменных, когда их зависимость выражается через дополнительную величину — параметр. Параметрическое представление для более общего случая: когда переменные связаны отношением в виде уравнения (или системы уравнений, если переменных больше двух).

Предел последовательности действительных чисел (определения последовательности)

В математике пределом последовательности называют объект, к которому члены последовательности в некотором смысле стремятся или приближаются с ростом номера. Последовательность — это набор элементов некоторого множества:

для каждого натурального числа можно указать элемент данного множества;

это число является номером элемента и обозначает позицию данного элемента в последовательности;

для любого элемента (члена) последовательности можно указать следующий за ним элемент последовательности.

В том случае, если последовательность {f(xn)} неограниченно возрастает (или убывает) при любом способе приближения x к своему пределу а, то будем говорить, что функция f(x) имеет бесконечный предел.

Критерии Коши (необходимое и достаточное условие существования конечного предела последовательности)

Теорема 2. (Необходимое и достаточное условия существования предела функции в точке.)

Пусть функция f(x) определена в некоторой окрестности точки x₀.

         Для того чтобы функция f(x) имела в точки x₀ предел необходимо и достаточно, чтобы функция f(x) в некоторой окрестности точки  x₀  была представима в виде      f(x)=A+a(x),

где   a(x) – бесконечно малая функция,  А – число.

Доказательство

Геометрический смысл конечного и бесконечного предела последовательности

Выясним геометрический смысл понятия предела последовательности. Расположим члены последовательности x₁,x₂,..., x_n,... на числовой прямой. Неравенство |x_n-A|<e равносильно следующему A- e < x_n < A + e, которое говорит о том, что члены последовательности x_n попадают в e - окрестность точки A. Вне этой e -окрестности может быть лишь конечное число членов данной последовательности

Ограниченная, бесконечно большая, бесконечно малая, сходящаяся, расходящаяся, монотонно возрастающая, монотонно убывающая последовательности (определения, примеры)

Последовательность   называется ограниченной сверху, если существует такое число   , что для любого номера   , 

Последовательность   называется ограниченной снизу, если существует такое число   , что для любого номера   , 

Последовательность   называется ограниченной, если она ограниченная сверху и ограниченная снизу, то есть существует такое число   , что для любого номера   ,  Последовательность   называется неограниченной, если существует такое число   , что существует такой номер   , что 

Определение (бесконечно большая последовательность). xn – бесконечно большая последовательность, если  c>0 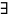  N:   n>N |x_n|>c.

Пример 1. Последовательности n, 2ⁿ являются бесконечно большими.

Определение (бесконечно малая последовательность). Бесконечно малая последовательность — последовательность, предел которой равен 0.

Пример . Последовательность xn = 1/n является бесконечно малой последовательностью.

Последовательность  называется сходящейся, если у нее существует конечный предел (т.е. существует    ).

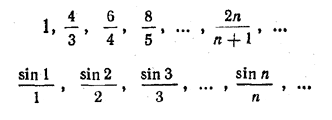
Числовая последовательность {x_n}  называется расходящейся, если она не имеет конечного предела, т.е. если она либо имеет бесконечный предел, либо у нее вообще нет предела. В частности всякая неограниченная числовая последовательность расходится.

Если числовая последовательность содержит две или более двух подпоследовательностей, сходящихся к различным пределам, она расходится.

Последовательность   элементов множества   называется возрастающей, если каждый следующий элемент этой последовательности превышает предыдущий. Пример(1,2,3…).

Последовательность   элементов множества   называется убывающей, если каждый элемент этой последовательности превышает следующий за ним. Пример(-1,-2,-3..).

Связь между бесконечно малыми и бесконечно большими последовательностями

Основные теоремы о сходящихся последовательностях (теорема о единственности предела, теорема об ограниченности сходящейся последовательности)

Определение конечного предела функции в точке по Гейне, по Коши (эквивалентность определений). Геометрический смысл

Определение предела функции в точке по Гейне. Число b называется пределом функции у = f(x) при х, стремящемся к а (или в точке а), если для любой последовательности {x_n}, сходящейся ка (стремящейся к а, имеющей пределом число а), причем ни при каком значении n х_n ≠ а, последовательность {y_n = f(x_n)} сходится к b.

Данные определения предполагают, что функция у = f(x) определена в некоторой окрестности точки а, кроме, быть может, самой точки а.

Геометрически существование предела функции в точке по Коши означает, что для любого числа e > 0 можно указать на координатной плоскости такой прямоугольник с основанием 2d > 0, высотой 2e и центром в точке (а; b), что все точки графика данной функции на интервале (а–d; а + d), за исключением, быть может, точки М(а; f(а)), лежат в этом прямоугольнике

Определение предела функции в точке по Коши.Число b называется пределом функции у = f(x) при х, стремящемся к а (или в точке а), если для любого положительного числа e существует такое положительное число d, что при всех х ≠ а, таких, что |x – a | < d, выполняется неравенство | f(x) – a | < e .