3.1. Опыт с неоднозначными исходами. Случайное событие

Теория вероятностей изучает закономерности, присущие опытам с неоднозначными исходами. Так называют опыты, результаты которых невозможно безошибочно предсказать. Например, при игре в рулетку шарик, брошенный на вращающееся колесо, может остановиться в любой из 37 пронумерованных лунок (0, 1, 36), но до остановки колеса номер лунки остается неизвестным.

Опыт и его исходы:

Понятия «опыт» и «исход» являются первичными понятиями теории вероятностей.

Опыт - это некоторая последовательность действий, которые выполняются при соблюдении определенных условий.

Исход - это то, что непосредственно получается в результате опыта.

В медицинских исследованиях опыт - это любое обследование пациента, например, определение содержания глюкозы в крови, взятой из вены. Исходом является результат обследования.

Случайное событие Отдельные исходы опыта, как правило, не имеют самостоятельной значимости. Практический интерес представляют некоторые их совокупности, которые называют событиями четного числа, и «проигрыш» - выпадение нечетного числа. Все остальное - не важно.

Исходы медицинских исследований тоже группируют в значимые события. Например, при определении содержания глюкозы в крови рассматриваются 3 события: данный показатель в норме (3,9-6,4 ммоль/л); ниже нормы; выше нормы. А вот конкретная величина показателя (например, 5,18 ммоль/л) практического значения не имеет. В этом примере событие «в норме» - совокупность всех чисел из интервала (3,9-6,4 ммоль/л).

Случайным событием или просто событием называется некоторая совокупность исходов опыта, имеющая практический интерес. Такие исходы называются благоприятствующими этому событию (или благоприятным для него).

Событие наступает, если результатом опыта является один из благоприятствующих исходов. В теории вероятностей случайные события обозначаются заглавными латинскими буквами (А, В, С...).

3.2. Действия над событиями. Противоположное событие.

НЕСОВМЕСТНЫЕ СОБЫТИЯ

Пример, поясняющий технику выполнения операций сложения и умножения событий. Бросается игральный кубик. Событие А - выпадение четного числа: А = {2, 4, 6}. Событие В - выпадение числа, кратного трем: B = {3, 6}.

• Сложение: А + В - это выпадение числа, которое или является четным, или делится на 3: А + В = {2, 3, 4, 6}.

• Произведение: АВ - это выпадение числа, которое является и четным, и делится на 3: АВ = {6}.

Несовместные события

Важное место в теории вероятности занимают несовместные события.

Несовместными называются события, которые не могут произойти одновременно (при выполнении одного опыта).

4. Случайные величины: Под случайной величиной (СВ) понимается величина, значение которой зависит от исходов опыта со случайными исходами, обязательно одно.

Случайные величины обозначают большими буквами (X, К..), а их значения - малыми буквами (x, y...).

Пример. Однократное бросание игральной кости. Возможные события заключаются в том, что на верхней грани выпадает Z: 1, 2, 3, 4, 5, 6.

Пример. Подбрасывается монета n раз. Возможные результаты: герб выпал 0, 1, 2, …, n раз.

Из множества всех случайных величин выделяют два наиболее часто встречающихся вида: дискретные и непрерывные.

Дискретная случайная величина - такая СВ, которая может принимать только конечное (или счетное) множество значений.

Эти значения нумеруются х1, х2, х3..., а вероятности их появления обозначаются p1, p2, p3...

Примеры дискретных величин с конечным множеством значений: число букв на случайно выбранной странице книги, энергия электрона в атоме, число зерен в колосе пшеницы и т.п.

Непрерывная случайная величина - такая СВ, которая может принимать любое значение в некотором определенном интервале (а, b)..

Соответствие между всеми возможными значениями дискретной случайной величины и их вероятностями называется законом распределения данной случайной величины

Ряд распределения:

Дискретная случайная величина считается заданной, если известны ее возможные значения х1, x2...xNи соответствующие им вероятности p1, p2...pN. Совокупность значений СВ и их вероятностей, заданная в виде таблицы, называется рядом распределения, или распределением дискретной случайной величины:

Сумма всех вероятностей равна единице:

Ряд распределения является самой полной характеристикой дискретной СВ.

Общие свойства функции распределения:

Кроме этого универсального, существуют также частные виды законов распределения: ряд распределения (только для дискретных случайных величин) и плотность распределения (только для непрерывных случайных величин).

Основные свойства плотности распределения:

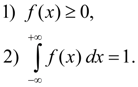
ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ВЕЛИЧИН

Математическое ожидание МХ случайной величины Х - это ее среднее арифметическое значение.

В это определение вкладывается следующий смысл. Пусть в серии из n опытов получены n значений случайной величины: х1, х2, ... хп. При неограниченном увеличении длины серии среднее арифметическое всех полученных значений стремится к МХ:

Возможные значения случайной величины рассеяны вокруг ее математического ожидания М(х): часть из них превышает М(х), часть - меньше М(х). Рассеяние значений случайной величины вокруг ее математического ожидания оценивают с помощью дисперсии.

Дисперсия - это математическое ожидание квадрата отклонения случайной величины от ее математического ожидания:

Формулы для расчета дисперсии дискретной и непрерывной случайных величин имеют следующий вид:

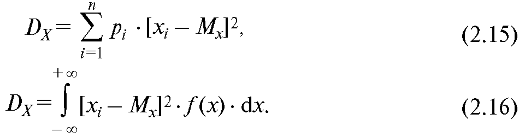При вычислении дисперсии отклонения значения случайной величины возводятся в квадрат. Это делается для подавления знака минус, который появляется в тех случаях, когда х < МХ. Если этого не делать, то отрицательные и положительные значения скомпенсируют друг друга и в результате получится ноль. Для того чтобы избавиться от последствий возведения отклонений в квадрат, после вычисления дисперсии из нее извлекают квадратный корень. Полученную при этом величину используют в качестве меры отклонения случайной величины от среднего значения.

Среднеквадратическое отклонение (СКО) случайной величины - это квадратный корень из ее дисперсии:

(иногда употребляют термин «стандартное отклонение»).

При обработке данных над случайными величинами выполняют математические действия, в результате которых получаются новые случайные величины. Покажем, как меняются при этом математические ожидания и дисперсии.

1. При сложении случайной величины с константой (С) константа добавляется к математическому ожиданию, а дисперсия и СКО не меняются:

2. При умножении (делении) случайной величины на константу (k) математическое ожидание умножается на константу, а дисперсия на ее квадрат:

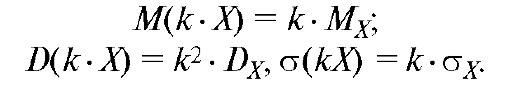
3.При сложении случайных величин (как независимых, так и зависимых) их математические ожидания складываются:

4. При сложении независимых случайных величин их дисперсии складываются:

Нормальный закон распределения (закон Гаусса)

Случайная величина ^распределена по нормальному закону, если она определена на всей числовой оси и ее плотность вероятности определяется формулой:

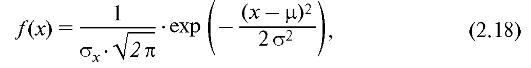
где μ = МХ - математическое ожидание случайной величины; σ - ее среднеквадратическое отклонение.

Важность нормального закона распределения для практической статистики связана с центральной предельной теоремой, согласно которой сумма большого числа независимых случайных величин с одинаковым законом распределения имеет распределение, которое можно считать нормальным. При этом закон распределения, которому подчиняются слагаемые, значения не имеет и может быть вообще не известен. Мы будем использовать это свойство в следующем параграфе.

На рис. 2.8 представлены графики плотности вероятности двух нормально распределенных СВ с μ = 0, σ = 2 и μ = 2, σ = 1. Отметим некоторые свойства этих графиков:

• график плотности распределения нормального закона имеет симметричный, колоколообразный вид; линия симметрии проходит через математическое ожидание случайной величины (х = μ);

• в точке х = μ функция достигает максимума;

• параметр σ характеризует форму кривой распределения: чем меньше σ, тем уже и выше график.

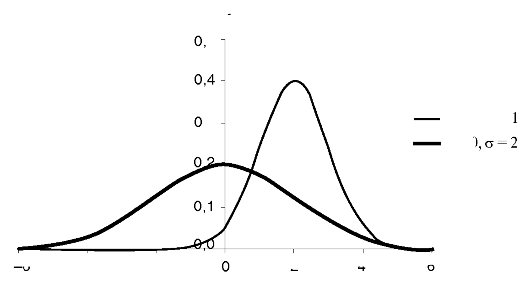
Рис. 2.8. Графики плотности вероятности нормального закона распределения

Для вычисления значений функции распределения и плотности вероятностей нормального закона используются компьютерные функции.

5. ОСНОВНЫЕ ПОНЯТИЯ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ

Математическая статистика - раздел математики, посвященный математическим методам обработки, систематизации и использования статистических данных для научных и практических выводов.

В медико-биологических задачах часто приходится исследовать распределение того или иного признака для очень большого числа индивидуумов. У разных индивидуумов этот признак имеет различное значение, поэтому он является случайной величиной. Например, любой лечебный препарата имеет различную эффективность при его применении к разным пациентам. Однако для того чтобы составить представление об эффективности данного препарата, нет необходимости применять его ко всем больным. Можно проследить результаты применения препарата к сравнительно небольшой группе больных и на основании полученных данных выявить существенные черты (эффективность, противопоказания) процесса лечения.

Генеральная совокупность - подлежащая изучению совокупность однородных элементов, характеризуемых некоторым признаком. Этот признак является непрерывной случайной величиной с плотностью распределения f(x).

Например, если нас интересует распространенность какого-либо заболевания в некотором регионе, то генеральная совокупность - все население региона. Если же мы хотим выяснить подверженность этому заболеванию мужчин и женщин по отдельности, то следует рассматривать две генеральные совокупности.

Для изучения свойств генеральной совокупности отбирают некоторую часть ее элементов.

Выборочная совокупность - часть генеральной совокупности, выбираемая для обследования (лечения).

Если это не вызывает недоразумений, то выборкой называют как совокупность объектов, отобранных для обследования, так и совокупность значений исследуемого признака, полученных при обследовании. Эти значения могут быть представлены несколькими способами.

Вариационными называют ряды распределения, построенные по количественному признаку. Значения количественных признаков у отдельных единиц совокупности непостоянны, более или менее различаются между собой.

Простой статистический ряд - значения исследуемого признака, записанные в том порядке, в котором они были получены.

Пример простого статистического ряда, полученного при измерении скорости поверхностной волны (м/с) в коже лба у 20 пациентов приведен в табл. 3.1.

Таблица 3.1. Простой статистический ряд

Простой статистический ряд - основной и самый полный способ записи результатов обследования. Он может содержать сотни элементов. Окинуть такую совокупность одним взглядом весьма затруднительно. Поэтому большие выборки обычно подвергают разбиению на группы. Для этого область изменения признака разбивают на несколько (N) интервалов равной ширины и подсчитывают относительные частоты (n/n) попадания признака в эти интервалы. Ширина каждого интервала равна:

Границы интервалов имеют следующие значения:

Если какой-то элемент выборки является границей между двумя соседними интервалами, то его относят к левому интервалу. Сгруппированные таким образом данные называют интервальным статистическим рядом.

Интервальный статистический ряд - это таблица, в которой приведены интервалы значений признака и относительные частоты попадания признака в эти интервалы.

В нашем случае можно образовать, например, такой интервальный статистический ряд (N = 5, d = 4), табл. 3.2.

Таблица 3.2. Интервальный статистический ряд

Здесь к интервалу 28-32 отнесены два значения равные 28 (табл. 3.1), а к интервалу 32-36 - значения 32, 33, 34 и 35.

Интервальный статистический ряд можно изобразить графически. Для этого по оси абсцисс откладывают интервалы значений признака и на каждом из них, как на основании, строят прямоугольник с высотой, равной относительной частоте. Полученная столбцовая диаграмма называется гистограммой.

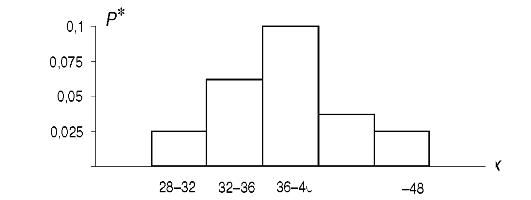
Рис. 3.1. Гистограмма

• На гистограмме статистические закономерности распределения признака просматриваются достаточно отчетливо.

• При большом объеме выборки (несколько тысяч) и малой ширине столбцов форма гистограммы близка к форме графика плотности распределения признака.

• Число столбцов гистограммы можно выбрать по следующей формуле:

• Построение гистограммы вручную - процесс долгий. Поэтому разработаны компьютерные программы для их автоматического построения.

Полигон частот

Другим распространенным способом графического представления является полигон частот.

Полигон частот образуется ломаной линией, соединяющей точки, соответствующие срединным значениям интервалов группировки и частотам этих интервалов, срединные значения откладываются по оси х, а частоты – по оси у.

Из сравнения двух рассмотренных способов графического представления эмпирических распределений следует, что для получения полигона частот из построенной гистограммы нужно середины вершин прямоугольников, образующих гистограмму, соединить отрезками прямых.

Мода — это наиболее часто встречающийся вариант ряда. Мода применяется, например, при определении размера одежды, обуви, пользующейся наибольшим спросом у покупателей. Модой для дискретного ряда является варианта, обладающая наибольшей частотой. При вычислении моды для интервального вариационного ряда необходимо сначала определить модальный интервал (по максимальной частоте), а затем — значение модальной величины признака по формуле:

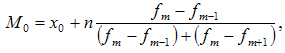
Медиана — это значение признака, которое лежит в основе ранжированного ряда и делит этот ряд на две равные по численности части.

Для определения медианы в дискретном ряду при наличии частот сначала вычисляют полусумму частот , а затем определяют, какое значение варианта приходится на нее. (Если отсортированный ряд содержит нечетное число признаков, то номер медианы вычисляют по формуле:

Ме = (n+ 1)/2,

в случае четного числа признаков медиана будет равна средней из двух признаков находящихся в середине ряда).

Выборочное среднее (Х) - это среднее арифметическое всех элементов простого статистического ряда:

Для нашего примера Х = 37,05 (м/с).

Выборочное среднее - это наилучшая оценка генерального среднего М.

Выборочная дисперсия s2 равна сумме квадратов отклонений элементов от выборочного среднего, поделенной на n - 1:

В нашем примере s2 = 25,2 (м/с)2.

Выборочная дисперсия - это наилучшая оценка генеральной дисперсии (σ2).

Выборочное среднеквадратическое отклонение (s) - это квадратный корень из выборочной дисперсии:

Для нашего примера s = 5,02 (м/с). Выборочное среднеквадратическое отклонение - это наилучшая оценка генерального СКО (σ)

6. ИНТЕРВАЛЬНАЯ ОЦЕНКА ГЕНЕРАЛЬНОГО СРЕДНЕГО ДЛЯ НОРМАЛЬНОГО ЗАКОНА РАСПРЕДЕЛЕНИЯ. Построение интервальной оценки генерального среднего М для генеральной совокупности с нормальным законом распределения основано на следующем свойстве. Для выборки объема n отношение 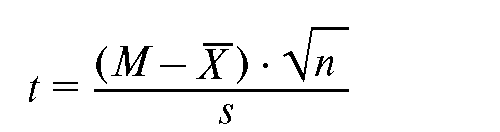подчиняется распределению Стьюдента с числом степеней свободы ν = n - 1. Здесь Х - выборочное среднее, а s - выборочное СКО.

Точечная оценка характеристик генеральной совокупности – наиболее простой, но не очень достоверный способ. При данном способе в качестве оценок характеристик генеральной совокупности используются соответствующие числовые характеристики выборки. Например, в качестве генерального среднего используется выборочное среднее, в качестве генеральной дисперсии – выборочная дисперсия и т.д. Такие оценки и называются точечными. Их недостаток состоит в том, что не ясно, насколько сильно они отличаются от истинных значений параметров генеральной совокупности. Ошибка может быть особенно большой в случае малых выборок/

Доверительный интервал для генеральной средней при известном значении среднего квадратического отклонения и при условии, что случайная величина (количественный признак ) распределена нормально, задается выражением

Доверительный интервал для генеральной средней нормального распределения признака при малой выборке: