
3. Зміст завдань і методичні рекомендації до їх виконання
Задача 1
Торгові фірма має намір придбати товар за 400 тисяч гривень, транспортувати його до місця реалізації (вартість транспортування 32 тисячі гривень) де на протязі 2 місяців має намір реалізувати його за 580 тисяч гривень.
Розрахуйте чистий дохід, ефективність та дохідність інвестиційного проекту.
Чистий дохід = 580-400-32 =
Ефективність: 580 / 432 =
Дохідність: [(580 – 432)*12] / (432*2) =
Задача 2
Підприємство має намір придбати технологічну лінію по виробництву валів. При якому мінімальному обороті це придбання окупиться якщо змінні витрати у перерахунку на один вал становлять 80 гривень, постійні витрати (оренда, комунальні платежі, заробітна плата та ін.) - 5000000 гривень на місяць. Вартість одного валу 120 гривень.
Точка беззбитковості BEP = 5000000 / (120-80) =
Задача 3
Річний обсяг закупівлі товару комерційною фірмою становить Cv=100 тисяч гривень, річний обсяг продажу – S=135 тисяч гривень. Щорічні витрати на оренду приміщення, упаковку, оплату праці персоналу складають Cc=28 тисяч гривень. Який мінімальний річний обсяг продажу при якому фірма не збитків (мінімальний річний оборот)?
З системи формул BEP = Cc / (1 – Cm) та Cm = Cv / S випливає наступна формула: BEP = Cc / [1 – (Cv / S)] =
Задача 4
Зробіть порівняльний аналіз графіків зміни нарощування капіталу при реалізації схем простих та складних процентів.
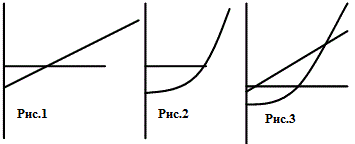
Прості проценти обраховуються за формулою: сума початкового капіталу * (1 + n*r), де n – кількість періодів, r – ставка. Складні проценти обраховуються за формулою: сума початкового капіталу * (1 + r)n.
Графік нарахування простих процентів – рис.1 (по осі х – роки, по осі у – гроші). Графік складних процентів – рис.2. При накладанні одного графіка на інший спостерігається наступне явище: за перший рік сума по простих процентах буде вищою за суму, нараховану по складних процентах (рис. 3).
Задача 5
Підприємство має на рахунку у банку 1,2 мільйони гривень. Банк нараховує 12,5 % річних. Існує пропозиція ввійти усім капіталом до спільного підприємства, при цьому прогнозується подвоєння капіталу через 5 років. Чи варто приймати таку пропозицію?
Розрахуємо дохідність даної пропозиції. З формули FV=PV(1+i)n маємо: 2400000 = 1200000 (1+і)5; 2=(1+і)5;
i = ?
Задача 6
У вашому розпорядженні 10 мільйонів гривень і хотіли б подвоїти цю суму через 5 років. Яким є мінімально прийнятне значення процентної ставки?
За формулою FV=PV(1+i)n (формула складних процентів): і = ?
За формулою FV=PV(1+in) [формула простих процентів]: і = ?
Задача 7
Фірмі необхідно накопичити 2 мільйони гривень для придбання через 10 років будівлі під офіс. Найбільш безпечним способом накопичення є придбання безризикових державних цінних паперів, що генерують річний дохід по ставці 8% річних при нарахуванні відсотків кожні півроку. Яким повинен бути початковий внесок фірми.
За формулою FV=PV(1+i)n (формула складних процентів) нам невідоме значення PV = ?
Задача 8
Розрахуйте теперішню вартість 1000 гривень які будуть отримані через 12 років маючи на увазі що ставка дисконтування (вартість капіталу, процентна ставка, дисконтна ставка, ставка капіталізації) становить 12 відсотків.
За формулою FV=PV(1+i)n маємо: PV = ?
Задача 9
Розрахуйте теперішню вартість 623 гривень, що будуть отримані через 8 років плюс 1092 гривень, які будуть отримані через 8 років після цього, за умови, що процентна ставка становить 7 відсотків.
За формулою FV=PV(1+i)n маємо: PV = ?
Задача 10
Розрахуйте теперішню вартість 10-ти річного ануїтету вартістю 100 гривень, за ставкою 20% річних.
За формулою PVa = X * [(1/i) + [1 / (i*(1+i)n)]] маємо: PVa = ?
Задача 11
Розрахуйте теперішню вартість 250 гривень отримуваних щорічно на протязі 21 року плюс 1200 гривень що будуть отримуватися довічно після 22 року за умови, що річна процентна ставка становитиме 11 відсотків.
За формулою обчислення ануїтету PVa = X * [(1/i) + [1 / (i*(1+i)n)]] розрахуємо теперішню вартість 250 гривень: PVa = ?
Задача 12
Фірма має намір придбати обладнання вартістю 20000 гривень. Розраховано, що річна економія від встановлення цього обладнання становитиме 5000 гривень, тривалість експлуатації становитиме 5 років а залишкова вартість 1000 гривень. Маючи на увазі, що показник норми дохідності, що вимагається становить 10%, які дії ви б порекомендували?
Розрахуємо показник NPV для даного проекту.
Рік |
0 |
1 |
2 |
3 |
4 |
5 |
CF, тис. грн. |
|
|
|
|
|
|
Дисконтний множник |
|
|
|
|
|
|
NPV |
|
|
|
|
|
|
Задача 13
Розрахуйте теперішню вартість проектів А і Б, маючи на увазі, що ставка дисконтування становить 0 відсотків, 10 відсотків та 20 відсотків.
|
Проект А |
Проект Б |
Початкові витрати (грн..) |
1200 |
1200 |
Надходження коштів (грн.) |
|
|
Рік 1 |
1000 |
100 |
Рік 2 |
500 |
600 |
Рік 3 |
100 |
1100 |
Який з проектів є кращим за кожної ставки дисконтування? Чому вони не дають однакових результатів?
За формулою NPV=[S (Xt/(1+k)t]-I, де Xt – величина чистого грошового потоку на кінець року t, k – ставка дисконтування, n – тривалість проекту, І – початкові інвестиції розрахуємо теперішню вартість даних проектів за кожної ставки дисконтування.
Проект |
NPV за відповідної ставки дисконтування |
||
0% |
10% |
20% |
|
А |
|
|
|
Б |
|
|
|
Задача 14
Керівництво компанії "Автосервіс" має намір прийняти рішення стосовно придбання автоматичної мийки для машин. Витрати на придбання, встановлення та пусконалагоджувальні роботи становлять приблизно 140 000 гривень. Очікувана тривалість експлуатації автомийки становить 7 років. Очікуваний річний балансовий прибуток буде наступним:
Рік |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
Операційний грошовий потік |
30000 |
50000 |
60000 |
60000 |
30000 |
20000 |
20000 |
Амортизація |
20000 |
20000 |
20000 |
20000 |
20000 |
20000 |
20000 |
Балансовий прибуток |
10000 |
30000 |
40000 |
40000 |
10000 |
-- |
-- |
На кінець сьомого року експлуатації залишкова вартість мийки становитиме кілька гривень. Компанія класифікує свої проекти наступним чином:
Норма дохідності, що вимагається |
|
Низький ризик |
20 % |
Середній ризик |
30 % |
Високий ризик |
40 % |
Проект встановлення автоматичної автомийки вважається таким, що має середній рівень ризику. Чи варто реалізовувати цей проект?
За формулою NPV=[S (Xt/(1+k)t]-I, де Xt – величина чистого грошового потоку на кінець року t, k – ставка дисконтування, n – тривалість проекту, І – початкові інвестиції розрахуємо теперішню вартість даного проекту за ставки дохідності 30%. NPV= ?
Задача 15
Керівництво фірми повинно прийняти рішення стосовно придбання нового обладнання. Початкові витрати на закупівлю монтаж та пусконалагоджувальні роботи становитимуть 140 000 гривень. Тривалість експлуатації обладнання становитиме 5 років, а очікуваний балансовий прибуток буде наступним:
Рік |
1 |
2 |
3 |
4 |
Операційний грошовий потік |
90 000 |
90 000 |
100 000 |
50 000 |
Амортизація |
50 000 |
30 000 |
40 000 |
20 000 |
Балансовий прибуток |
40 000 |
60 000 |
60 000 |
30 000 |
По закінченні п'ятого року експлуатації залишкова вартість обладнання становитиме лише декілька гривень. Компанія класифікує свої проекти наступним чином:
Очікувана норма дохідності |
|
Низький ризик |
16% |
Середній ризик |
24% |
Високий ризик |
30% |
Перерахуйте найбільш розповсюджені методи оцінки інвестиційних пропозицій.
Чи варто фірмі купляти нове обладнання?
За формулою NPV=[S (Xt/(1+k)t]-I, де Xt – величина чистого грошового потоку на кінець року t, k – ставка дисконтування, n – тривалість проекту, І – початкові інвестиції розрахуємо теперішню вартість даного проекту за ставки дохідності 24%. NPV= ?
Задача 16
Проект, що потребує інвестицій у розмірі 160 000 гривень передбачає отримання річного доходу у розмірі 30 000 гривень на протязі 15 років. Оцініть доцільність такої інвестиції, якщо коефіцієнт дисконтування 15%.
Розрахуємо теперішню вартість ануїтету за умовами даної задачі. За формулою PVa = X * [(1/i) + [1 / (i*(1+i)n)]] маємо: PVa=?
Задача 17
Аналізуються проекти (грн.)
|
ІС |
С1 |
С2 |
А |
-4000 |
2500 |
3000 |
Б |
-2000 |
1200 |
1500 |
Ранжуйте проекти за критеріями IRR, PP, NPV якщо r =10%.
Обчислимо NPV цих проектів NPV=[S (Xt/(1+k)t]-I.
NPVA=?
NPVБ=?
Показник РР (період окупності) визначається шляхом додавання позитивних грошових потоків проекту до моменту рівності цієї суми початковим витратам.
IRR обчислюється за формулою: 0 = S[Rt/(1+r)t]-C, де Rt – очікувані чисті грошові потоки, t – кількість періодів, r – ставка дохідності, C – початкові витрати капіталу. Отже, за проектом А показник IRR матиме значення: ?
Задача 18
Для кожного з наведених нижче проектів розрахуйте IRR та NPV якщо значення коефіцієнту дисконтування становить 20%. Оцініть проекти та ранжуйте їх.
А |
-370 |
-- |
-- |
-- |
-- |
1000 |
Б |
-240 |
60 |
60 |
60 |
60 |
-- |
В |
-263,5 |
100 |
100 |
100 |
100 |
100 |
Розглянемо проект А. NPV=[S (Xt/(1+k)t]-I=[1000/(1+0.2)5]-370=31.6. IRR: 0 = S[Rt/(1+r)t]-C, де Rt – очікувані чисті грошові потоки, t – кількість періодів, r – ставка дохідності, C – початкові витрати капіталу.
Розглянемо проект Б.
Розглянемо проект В.
Рік |
CF |
PV при 20% |
PV при 30% |
PV при 24% |
PV при 28% |
PV при 26% |
PV при 28% |
0 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Обчислимо IRR за формулою IRR=r1+[f(r1)/(f(r1)-f(r2))]*(r1-r2
Задача 19
Проаналізуйте два альтернативних проекти якщо ціна капіталу 10%:
А |
-100 |
120 |
|
|
|
Б |
-100 |
-- |
-- |
-- |
174 |
Розглянемо проект А. NPV=[S (Xt/(1+k)t]-I?
IRR: 0 = S[Rt/(1+r)t]-C;
РІ (індекс прибутковості) = S[Rt/(1+r)t]/C
РР (період окупності – це мінімальний період, за який CF>=C)
DPP (дисконтований період окупності – мінімальний період, за який [CF/(1+r)n>=C
Розглянемо проект Б.
Задача 20
Розрахуйте IRR проекту:
А |
-200 |
20 |
40 |
60 |
60 |
80 |
Застосуємо метод послідовних ітерацій (в колонках “PV при...” – дисконтовані грошові потоки).
Рік |
CF |
PV при 5% |
PV при 10% |
PV при 7% |
PV при 8% |
0 |
-200 |
-200 |
-200 |
-200 |
-200 |
1 |
20 |
19,04 |
18,2 |
18,7 |
18,52 |
2 |
40 |
36,4 |
33,04 |
34,92 |
34,3 |
3 |
60 |
51,84 |
45,06 |
49 |
47,64 |
4 |
60 |
49,38 |
41 |
45,8 |
44,1 |
5 |
80 |
62,72 |
49,7 |
57,04 |
54,5 |
|
|
S = 19,38 |
S = -13 |
S = 5,46 |
S = -0,94 |
IRR = r1+[f(r1)/(f(r1)-f(r2))]*(r1-r2)
Задача 21
Порівняйте за критеріями IRR, PP та NPV два проекти, якщо ціна капіталу становить 13%:
А |
-20 000 |
7 000 |
7 000 |
7 000 |
7 000 |
Б |
-25 000 |
2 500 |
5 000 |
10 000 |
20 000 |
Розглянемо проект А.
NPV=[S (Xt/(1+k)t]-I
РР (період окупності – це мінімальний період, за який CF>=C)
IRR розрахуємо методом послідовних ітерацій. (в колонках “PV при...” – дисконтовані грошові потоки).
Рік |
CF |
PV при 10% |
PV при 15% |
PV при 14% |
0 |
|
|
|
|
1 |
|
|
|
|
2 |
|
|
|
|
3 |
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
IRR = r1+[f(r1)/(f(r1)-f(r2))]*(r1-r2)
Розглянемо проект Б.
NPV = [S(Xt/(1+k)t] – I
IRR розрахуємо методом послідовних ітерацій.
Рік |
CF |
PV при 15% |
PV при 20% |
PV при 24% |
PV при 22% |
PV при 23% |
0 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
IRR = r1+[f(r1)/(f(r1)-f(r2))]*(r1-r2)
Задача 22
Величина початкових інвестицій по проекту становить 18 000 гривень; очікувані доходи: у перший рік - 1 500 гривень, у наступні роки - по 3 600 гривень щорічно. Оцініть доцільність прийняття проекту, якщо вартість капіталу 10%.
Розрахуємо теперішню вартість даного проекту, використовуючи формулу розрахунку PV довічного ануїтету:
PVa = X*[1 / (i*(1+i)n)]. PV
Задача 23
Підприємство розглядає доцільність придбання нової технологічної лінії. На ринку є дві моделі з наступними параметрами:
|
Л1 |
Л2 |
Ціна |
9500 |
13000 |
Генерований річний дохід |
2100 |
2250 |
Строк експлуатації |
8 років |
12 років |
Ліквідаційна вартість |
500 |
800 |
Очікувана норма прибутку |
11% |
11% |
Обгрунтуйте доцільність тієї чи іншої технологічної лінії.
Розглянемо лінію Л1. Її теперішню вартість розрахуємо за формулою PV ануїтету: NPV=ГРД*[(1-(1+r)-n-1)/r] + [(ГРД+лікв.вартість)/(1+r)n]-I
Розглянемо лінію Л2. аналогічно
Задача 24
Знайдіть IRR грошового потоку: -100, +230,-132.
Застосуємо метод послідовних ітерацій (в колонках “PV при...” – дисконтовані грошові потоки за відповідної ставки).
Рік |
CF |
PV при 1% |
PV при 0,5% |
PV при 10% |
PV при 9% |
0 |
|
|
|
|
|
1 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
IRR = r1+[f(r1)/(f(r1)-f(r2))]*(r1-r2)
Задача 25
Якому з наведених проектів слід віддати перевагу якщо вартість капіталу 8%?
А |
-250 |
60 |
140 |
120 |
|
Б |
-300 |
100 |
100 |
100 |
100 |
Розглянемо проект А.
NPV=[S (Xt/(1+k)t]-I
РР (період окупності – це мінімальний період, за який CF>=C
РІ (індекс прибутковості) = S[Rt/(1+r)t]/C
DPP (дисконтова ний період окупності – мінімальний період, за який [CF/(1+r)n>=C)
IRR розрахуємо методом послідовних ітерацій (в колонках “PV при...” – дисконтовані грошові потоки).
Рік |
CF |
PV при 10% |
PV при 20% |
PV при 15% |
PV при 12% |
PV при 13% |
0 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
IRR = r1+[f(r1)/(f(r1)-f(r2))]*(r1-r2)
Розглянемо проект Б. аналогічно
Задача 26
Проаналізуйте два альтернативних проекти якщо ціна капіталу 10%
А |
-100 |
50 |
70 |
|
Б |
-100 |
30 |
40 |
60 |
Розглянемо проект А. NPV=[S (Xt/(1+k)t]-I
РР (період окупності – це мінімальний період, за який CF>=C)
РІ (індекс прибутковості) = S[Rt/(1+r)t]/C
DPP (дисконтова ний період окупності – мінімальний період, за який [CF/(1+r)n>=C
IRR розрахуємо методом послідовних ітерацій (в колонках “PV при...” – дисконтовані грошові потоки).
Рік |
CF |
PV при 10% |
PV при 15% |
PV при 12% |
PV при 13% |
0 |
|
|
|
|
|
1 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
IRR = r1+[f(r1)/(f(r1)-f(r2))]*(r1-r2)
Розглянемо проект Б. аналогічно
Задача 27
Наведені дані по двом проектам (тис. грн.):
П1 |
-10 |
5 |
3 |
2 |
4 |
П2 |
-10 |
2 |
3 |
5 |
4 |
(1) Який критерій не дає різниці по цим двом проектам?
(2) Не виконуючи спеціальних розрахунків дайте відповіді на питання: а) чи однакові значення IRR для цих проектів; б) якщо IRR різні, то який проект має більше значення IRR і чому. Обґрунтуйте відповіді.
Не дає різниці критерій РР (строк окупності) – в обох випадках він дорівнює 3 роки. Значення IRR по цих проектах не є однаковими: воно більше для проекту П1, адже [5/(1+i)1]>[5/(1+i)3], а грошовий потік із значенням “5” є найбільшим.
Задача 28
Є дані про чотири проекти:
Рік |
П1 |
П2 |
П3 |
П4 |
0 |
-10000 |
-13000 |
-10000 |
-6000 |
1 |
6000 |
8000 |
5000 |
5000 |
2 |
6000 |
8000 |
5000 |
2000 |
3 |
2000 |
1000 |
5000 |
2000 |
За припущення, що вартість капіталу становить 12%, дайте відповідь на наступні запитання:
(1) Який проект має найбільше значення NPV? (2)Який проект має найменше значення NPV? (3)Чому дорівнює значення IRR проекту П1? (4)Чому рівне значення IRR проекту П1, якщо грошові потоки третього року вважаються надзвичайно не передбачуваними і тому повинні бути виключеними з розрахунку?
NPV = [S(Xt/(1+k)t]-I.
Отже, найбільше значення NPV має проект П3, а найменше – проект П2.
IRR проекту П1 розрахуємо за допомогою методу послідовних ітерацій (в колонках “PV при...” – дисконтовані грошові потоки).
Рік |
CF |
PV при 20% |
PV при 25% |
PV при 22% |
PV при 23% |
0 |
|
|
|
|
|
1 |
|
|
|
|
|
2 |
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
IRR = r1+[f(r1)/(f(r1)-f(r2))]*(r1-r2)
IRR проекту П1 за умови непередбачуваності грошового потоку третього року знайдемо аналогічно.
Рік |
CF |
PV при 15% |
PV при 13% |
PV при 12% |
0 |
|
|
|
|
1 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
IRR = r1+[f(r1)/(f(r1)-f(r2))]*(r1-r2)
Задача 29
Проект Х має очікуваний дохід у розмірі 2000 гривень і значення стандартного відхилення 400 грн. Проект У має значення очікуваного доходу 1000 грн. і стандартне відхилення 400 грн. Який проект є більш ризиковим? Обгрунтуйте відповідь.
За проектом Х ризиковість буде aХ=400/2000=?, а за проектом У - aУ=400/1000=?
Задача 30
Значення розподілу ймовірності NPV для проектів Х та У наведено у таблиці:
Ймовірність |
Проект Х (грн.) |
Проект У (грн.) |
0,2 |
2 000 |
0 |
0,6 |
3 000 |
3 000 |
0,2 |
4 000 |
6 000 |
Розрахуйте очікуване значення NPV, стандартне відхилення та коефіцієнт варіації для кожного проекту. Який з цих проектів, що виключають один одного, варто прийняти?
Розглянемо проект Х.
Ймовірність |
0,2 |
0,6 |
0,2 |
|
Наслідок |
2000 |
3000 |
4000 |
|
NPV |
400 |
1800 |
800 |
S = 3000 |
Відхилення |
-1000 |
0 |
1000 |
|
Квадратичне відхилення |
1000000 |
0 |
1000000 |
|
Дисперсія=ймов.*кв.відх |
200000 |
0 |
200000 |
s2Х = 400000; sХ = 632,46 |
Коеф. варіації |
CV = s/SNPV =? |
|||
Розглянемо проект У.
Ймовірність |
0,2 |
0,6 |
0,2 |
|
Наслідок |
0 |
3000 |
6000 |
|
NPV |
0 |
1800 |
1200 |
S = 3000 |
Відхилення |
-3000 |
0 |
3000 |
|
Квадратичне відхилення |
9000000 |
0 |
9000000 |
|
Дисперсія |
1800000 |
0 |
1800000 |
s2Х = 3600000; sХ = 1897,37 |
Коеф. варіації |
CV = s/SNPV = ? |
|||
Оцінювання знань студентів заочної форми навчання здійснюється на основі результатів підсумкового контролю – екзамен - за 100-бальною шкалою оцінок.
