12,13) Если тело некоторой массы m двигалось под действием приложенных сил, и его скорость изменилась от до то силы совершили определенную работу a.

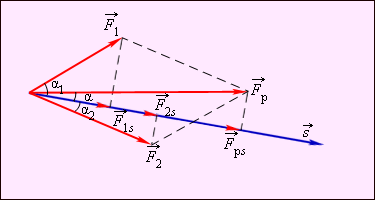
Работа всех приложенных сил равна работе равнодействующей силы (см. рис. 1.19.1).

Рисунок 1.19.1. Работа равнодействующей силы. . A = F1s cos α1 + F2s cos α2 = F1ss + F2ss = Fрss = Fрs cos α

Между изменением скорости тела и работой, совершенной приложенными к телу силами, существует связь. Эту связь проще всего установить, рассматривая движение тела вдоль прямой линии под действием постоянной силы В этом случае векторы силы перемещения скорости и ускорения направлены вдоль одной прямой, и тело совершает прямолинейное равноускоренное движение. Направив координатную ось вдоль прямой движения, можно рассматривать F, s, υ и a как алгебраические величины (положительные или отрицательные в зависимости от направления соответствующего вектора). Тогда работу силы можно записать как A = Fs. При равноускоренном движении перемещение s выражается формулой

Отсюда следует, что

Это выражение показывает, что работа, совершенная силой (или равнодействующей всех сил), связана с изменением квадрата скорости (а не самой скорости).

Физическая величина, равная половине произведения массы тела на квадрат его скорости, называется кинетической энергией тела:

Работа приложенной к телу равнодействующей силы равна изменению его кинетической энергии.

Это утверждение называют теоремой о кинетической энергии. Теорема о кинетической энергии справедлива и в общем случае, когда тело движется под действием изменяющейся силы, направление которой не совпадает с направлением перемещения.

Кинетическая энергия – это энергия движения. Кинетическая энергия тела массой m, движущегося со скоростью равна работе, которую должна совершить сила, приложенная к покоящемуся телу, чтобы сообщить ему эту скорость:

Если тело движется со скоростью то для его полной остановки необходимо совершить работу

В физике наряду с кинетической энергией или энергией движения важную роль играет понятие потенциальной энергии или энергии взаимодействия тел.

Потенциальная энергия определяется взаимным положением тел (например, положением тела относительно поверхности Земли). Понятие потенциальной энергии можно ввести только для сил, работа которых не зависит от траектории движения и определяется только начальным и конечным положениями тела. Такие силы называются консервативными.

Работа консервативных сил на замкнутой траектории равна нулю. Это утверждение поясняет рис. 1.19.2.

Свойством консервативности обладают сила тяжести и сила упругости. Для этих сил можно ввести понятие потенциальной энергии.

Рисунок 1.19.2. Работа консервативной силы A1a2 = A1b2. Работа на замкнутой траектории A = A1a2 + A2b1 = A1a2 – A1b2 = 0

Если тело перемещается вблизи поверхности Земли, то на него действует постоянная по величине и направлению сила тяжести Работа этой силы зависит только от вертикального перемещения тела. На любом участке пути работу силы тяжести можно записать в проекциях вектора перемещения на ось OY, направленную вертикально вверх:

ΔA = Fт Δs cos α = –mgΔs y,

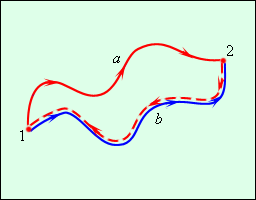
где F_т = F_тy = –mg – проекция силы тяжести, Δs_y – проекция вектора перемещения. При подъеме тела вверх сила тяжести совершает отрицательную работу, так как Δs_y > 0. Если тело переместилось из точки, расположенной на высоте h₁, в точку, расположенную на высоте h₂ от начала координатной оси OY (рис. 1.19.3), то сила тяжести совершила работу

A = –mg (h2 – h1) = –(mgh2 – mgh1).

Рисунок 1.19.3. Работа силы тяжести

Эта работа равна изменению некоторой физической величины mgh, взятому с противоположным знаком. Эту физическую величину называют потенциальной энергией тела в поле силы тяжести

Eр = mgh.

Она равна работе, которую совершает сила тяжести при опускании тела на нулевой уровень.

Работа силы тяжести равна изменению потенциальной энергии тела, взятому с противоположным знаком.

A = –(Eр2 – Eр1).

Потенциальная энергия E_р зависит от выбора нулевого уровня, т. е. от выбора начала координат оси OY. Физический смысл имеет не сама потенциальная энергия, а ее изменение ΔE_р = E_р2 – E_р1 при перемещении тела из одного положения в другое. Это изменение не зависит от выбора нулевого уровня.

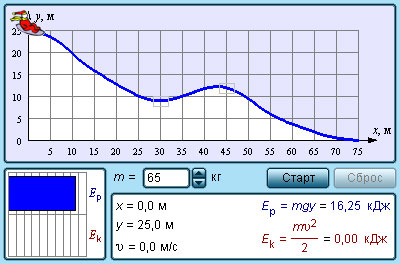
Модель. Кинетическая и потенциальная энергия

Если рассматривать движение тел в поле тяготения Земли на значительных расстояниях от нее, то при определении потенциальной энергии необходимо принимать во внимание зависимость силы тяготения от расстояния до центра Земли (закон всемирного тяготения). Для сил всемирного тяготения потенциальную энергию удобно отсчитывать от бесконечно удаленной точки, т. е. полагать потенциальную энергию тела в бесконечно удаленной точке равной нулю. Формула, выражающая потенциальную энергию тела массой m на расстоянии r от центра Земли, имеет вид (см. §1.24):

где M – масса Земли, G – гравитационная постоянная.

Понятие потенциальной энергии можно ввести и для силы упругости. Эта сила также обладает свойством консервативности. Растягивая (или сжимая) пружину, мы можем делать это различными способами.

Можно просто удлинить пружину на величину x, или сначала удлинить ее на 2x, а затем уменьшить удлинение до значения x и т. д. Во всех этих случаях сила упругости совершает одну и ту же работу, которая зависит только от удлинения пружины x в конечном состоянии, если первоначально пружина была недеформирована. Эта работа равна работе внешней силы A, взятой с противоположным знаком (см. §1.18):

где k – жесткость пружины. Растянутая (или сжатая) пружина способна привести в движение прикрепленное к ней тело, т. е. сообщить этому телу кинетическую энергию. Следовательно, такая пружина обладает запасом энергии. Потенциальной энергией пружины (или любого упруго деформированного тела) называют величину

Потенциальная энергия упруго деформированного тела равна работе силы упругости при переходе из данного состояния в состояние с нулевой деформацией.

Если в начальном состоянии пружина уже была деформирована, а ее удлинение было равно x₁, тогда при переходе в новое состояние с удлинением x₂ сила упругости совершит работу, равную изменению потенциальной энергии, взятому с противоположным знаком:

Потенциальная энергия при упругой деформации – это энергия взаимодействия отдельных частей тела между собой посредством сил упругости.

Свойством консервативности наряду с силой тяжести и силой упругости обладают некоторые другие виды сил, например, сила электростатического взаимодействия между заряженными телами. Сила трения не обладает этим свойством. Работа силы трения зависит от пройденного пути. Понятие потенциальной энергии для силы трения вводить нельзя.

14) При описании движения твердого тела важными понятиями являются момент силы и момент импульса. Пусть O – какая-то точка, относительно которой рассматриваются моменты вектора силы или вектора импульса, ее называют началом или полюсом. Обозначим через радиус-вектор, проведенный из этой точки к точке приложения силы . Моментом силы относительно точки О называется векторное произведение радиус-вектора на силу : . Из определения следует, что момент не изменится, если точку приложения силы перенести в любую другую точку, расположенную на линии действия силы (площади параллелограммов, построенных на векторах и , равны между собой). Если на материальную точку действует несколько сил, то равнодействующая этих сил равна их геометрической сумме. Пусть на материальную точку действуют две силы и , тогда равнодействующая этих сил будет . На основании свойств векторного произведения можно написать . Это означает, что момент равнодействующей двух или нескольких сил относительно некоторого начала равен геометрической сумме моментов составляющих сил относительно того же начала. Аналогично определяется момент импульса материальной точки относительно полюса О. Так называется векторное произведение . (1.4) Момент импульса и момент силы связаны между собой. Чтобы найти эту связь, продифференцируем выражение (3.1) по времени, тогда получим . Точка над буквой означат первую производную по времени. Так как начало О неподвижно, то – скорость материальной точки, связанная с импульсом соотношением . Поэтому первое слагаемое равно нулю, как векторное произведение коллинеарных векторов и . Второе слагаемое можно преобразовать с помощью уравнения Ньютона . Тогда получится или . (1.5) Это соотношение называется уравнением моментов: производная по времени момента импульса материальной точки относительно неподвижного начала равна моменту действующей силы относительно того же начала. Уравнение моментов (1.5) можно обобщить на случай произвольной системы материальных точек. Моментом импульса системы материальных точек относительно некоторого начала называется векторная сумма моментов импульсов всех материальных точек системы относительно того же начала. Аналогично момент всех действующих на систему материальных точек сил определяется как векторная сумма моментов отдельных сил. Вместо того, чтобы складывать моменты всех сил, можно сначала найти равнодействующую этих сил, а затем вычислить ее момент, также можно поступать и при нахождении импульса системы материальных точек. Предполагая начало неподвижным, напишем уравнение моментов для каждой материальной точки , где – суммарный момент всех внутренних сил, действующих на i-ю материальную точку, а затем векторно сложим их. Полный момент внутренних сил относительно любого начала равен нулю. Это объясняется тем, что внутренние силы всегда входят попарно: силе , с которой k-я точка действует i-ю, соответствует равная и противоположно направленная сила , с которой i-я точка действует на k-ю. При вычислении моментов этих сил точки их приложения можно перенести в одну и ту же точку на этой прямой. Тогда силы взаимно уничтожаются, а их полный момент будет равен нулю. Таким образом, третий закон Ньютона позволяет исключить из уравнения моментов для системы материальных точек внутренние силы. Для системы материальных точек уравнение моментов имеет следующий вид: , (1.6) то есть производная по времени от момента импульса системы материальных точек относительно произвольного неподвижного начала равна геометрической сумме моментов всех внешних сил относительно того же начала. Момент сил и момент импульса зависят не только от величины и направления этих векторов, но и от положения начала. Оба момента, вообще говоря, изменятся, если перейти к новому началу. Пусть О и О' – два неподвижных начала. Радиус-векторы и одной и той же точки относительно этих начал связаны соотношением , где – радиус-вектор начала О относительно О'. Написав выражения для моментов импульса каждой материальной точки системы и просуммировав эти выражения по всем материальным точкам, получим , или , где – полный импульс системы, и – моменты ее импульса относительно начал О и О' соответственно. Если импульс равен нулю, то . В этом случае вектор момента импульса не зависит от выбора начала. Аналогично, , где и – моменты сил, действующих на систему относительно начал О и О', а – геометрическая сумма этих сил. Если результирующая сила равна нулю, то . Это имеет место, например, для пары сил, то есть двух равных, но противоположно направленных сил, линии действия которых смещены одна относительно другой. Вот почему можно говорить о моменте пары сил, не указывая начала, относительно которого этот момент берется.

15,16) Пусть некоторая точка, относительно которой мы будем находить момент вектора силы или вектора импульса. Ее (точку) называют началом или полюсом. – вектор, проведенный из полюса к точке приложения силы. Момент силы относительно точки – произведение радиус-вектора на силу : .

 

Момент не изменится, если точку приложения силы перенести в любую другую точку, расположенную на линии действия силы.

Момент нескольких сил относительно точки – сумма моментов сил относительно той же точки. Момент силы относительно точки – произведение радиус-вектора на импульс : . Производная по времени будет выглядеть так: . Т.к. мы считаем неподвижной, то , а и мы получим , т.е. .

 

Последнее равенство – уравнение моментов.

 

Для системы материальных точек моменты всех внутренних сил равны нулю и мы можем записать уравнение моментов для множества материальных точек так: – производная момента импульса системы материальных точек по времени относительно неподвижного полюса равна геометрической сумме моментов всех внешних сил относительно того же полюса.

 

Закон сохранения момента импульса так же вытекает из этого уравнения – если сумма моментов всех внешних сил равна нулю относительно какого-то полюса, то момент импульса системы материальных точек относительно того же полюса будет постоянным во времени.

– эквивалентно , , . и – моменты импульса и силы относительно оси (проекции и на эту ось ) .

  – уравнение моментов относительно неподвижной оси (предполагается, что начало лежит на этой оси). Если момент всех внешних сил, относительно какой либо неподвижной оси равен нулю, то момент импульса относительно этой же оси будет постоянным. Пусть неподвижная ось – ось вращения, а материальная точка вращается вокруг нее по окружности с радиусом . Тогда момент импульса относительно оси вращения равен . Если угловая скорость, то  и . Если же вокруг оси вращается система материальных точек с одинаковой угловой скоростью , то .

– момент инерции системы относительно оси. С учетом этого получаем . Если же система материальных точек не только вращается, а принимает участие еще в каких то перемещениях (т.е. перестает быть постоянной), то уравнение трансформируется в соответствии с изменением мгновенной конфигурации системы:   .