Закон всемирного тяготения

Считается, что стержнем динамики Ньютона является понятие силы, а основная задача динамики заключается в установлении закона из данного движения и, наоборот, в определении закона движения тел по данной силе. Из законов Кеплера Ньютон вывел существование силы, направленной к Солнцу, которая была обратно пропорциональна квадрату расстояния планет от Солнца. Обобщив идеи, высказанные Кеплером, Гюйгенсом, Декартом, Борелли, Гуком, Ньютон придал им точную форму математического закона, в соответствии с которым утверждалось существование в природе силы всемирного тяготения, обусловливающей притяжение тел. Сила тяготения прямо пропорциональна произведению масс тяготеющих тел и обратно пропорционально квадрату расстояния между ними или математически:

Данный закон описывает взаимодействие любых тел – важно лишь то, чтобы расстояние между телами было достаточно велико по сравнению с их размерами, это позволяет принимать тела за материальные точки. В ньютоновской теории тяготения принимается, что сила тяготения передается от одного тяготеющего тела к другому мгновенно, при чем без посредства каких бы то ни было сред. Закон всемирного тяготения вызвал продолжительные и яростные дискуссии. Это не было случайно, поскольку этот закон имел важное философское значение. В законе всемирного тяготения наука получила образец закона природы как абсолютно точного, повсюду применимого правила, без исключений, с точно определенными следствиями.

Границы применимости

Вследствие развития физики в начале XX века определилась область применения классической механики: ее законы выполняются для движений, скорость которых много меньше скорости света. Было установлено, что с ростом скорости масса тела возрастает. Вообще законы классической механики Ньютона справедливы для случая инерциальных систем отсчета. В случае неинерциальных систем отсчета ситуация иная. При ускоренном движении неинерциальной системы координат относительно инерциальной системы первый закон Ньютона (закон инерции) в этой системе не имеет места, – свободные тела в ней будут с течением времени менять свою скорость движения. Первое несоответствие в классической механике было выявлено, тогда когда был открыт микромир. В классической механике перемещения в пространстве и определение скорости изучались вне зависимости от того, каким образом эти перемещения реализовывались. Применительно к явлениям микромира подобная ситуация, как выявилось, невозможна принципиально. Здесь пространственно-временная локализация, лежащая в основе кинематики, возможна лишь для некоторых частных случаев, которые зависят от конкретных динамических условий движения. В макро масштабах использование кинематики вполне допустимо. Для микро масштабов, где главная роль принадлежит квантам, кинематика, изучающая движение вне зависимости от динамических условий, теряет смысл.

Для масштабов микромира и второй закон Ньютона оказался несостоятельным – он справедлив лишь для явлений большого масштаба. Выявилось, что попытки измерить какую-либо величину, характеризующую изучаемую систему, влечет за собой неконтролируемое изменение других величин, характеризующих данную систему: если предпринимается попытка установить положение в пространстве и времени, то это приводит к неконтролируемому изменению соответствующей сопряженной величины, которая определяет динамическое состояние системы. Так, невозможно точно измерить в одно и то же время две взаимно сопряженные величины. Чем точнее определяется значение одной величины, характеризующей систему, тем более неопределенным оказывается значение сопряженной ей величины. Это обстоятельство повлекло за собой существенное изменение взглядов на понимание природы вещей.

Несоответствие в классической механики исходило из того, что будущее в известном смысле полностью содержится в настоящем – этим и определяется возможность точного предвидения поведения системы в любой будущий момент времени. Такая возможность предлагает одновременное определение взаимно сопряженных величин. В области микромира это оказалось невозможным, что и вносит существенные изменения в понимание возможностей предвидения и взаимосвязи явлений природы: раз значение величин, характеризующих состояние системы в определенный момент времени, можно установить лишь с долей неопределенности, то исключается возможность точного предсказания значений этих величин в последующие моменты времени, т.е. можно лишь предсказать вероятность получения тех или иных величин.

Другое открытие пошатнувшее устои классической механики, было создания теории поля. Классическая механика пыталась свести все явления природы к силам, действующим между частицами вещества, – на этом основывалась концепция электрических жидкостей. В рамках этой концепции реальными были лишь субстанция и ее изменения – здесь важнейшим признавалось описание действия двух электрических зарядов с помощью относящихся к ним понятий. Описание же поля между этими зарядами, а не самих зарядов было весьма существенным для понимания действия зарядов. Вот простой пример нарушения третьего закона Ньютона в таких условиях: если заряженная частица удаляется от проводника, по которому течет ток, и соответственно вокруг него создано магнитное поле, то результирующая сила, действующая со стороны заряженной частицы на проводник с током в точности равна нулю.

Созданной новой реальности места в механической картине мира не было. В результате физика стала иметь дело с двумя реальностями – веществом и полем. Если классическая физика строилась на понятии вещества, то с выявлением новой реальности физическую картину мира приходилось пересматривать. Попытки объяснить электромагнитные явления с помощью эфира оказалось несостоятельными. Эфир экспериментально обнаружить не удалось. Это привело к созданию теории относительности, заставившей пересмотреть представления о пространстве и времени, характерные для классической физики. Таким образом, две концепции – теория квантов и теория относительности – стали фундаментом для новых физических концепций.

4) Таким образом, можно утверждать, что при отсутствии воздействия других тел, тело продолжает двигаться с постоянной скоростью, сохраняет скорость своего движения. Свойство тел сохранять свою скорость называется инерцией, а свободное движение тел называют движением по инерции. Сформулированной утверждение в физике носит название закона инерции Галилея.

Отметим, что, когда говорят о движении с постоянной скоростью, подразумевают постоянство скорости, как по величине, так и по направлению. Вспомните, как трудно повернуть на гладком льду - не хватает внешних сил, способных изменить направление скорости. Говоря в дальнейшем о равномерном движении, мы будем подразумевать движение с постоянной скоростью, как по величине, так и по направлению.

В разделе «Кинематика» мы неоднократно подчеркивали, что механическое движение относительно - имеет смысл говорить только о движении одного тела относительно другого. Поэтому, в формулировке закона инерции Г.Галилея мы упустили одну существенную деталь – относительно какой системы отсчета рассматривается движение. Не трудно привести пример системы отсчета, в которой закон инерции не выполняется. Пусть поезд начинает отходить ускоренно от вокзала, в системе отсчета, связанной с поездом, вокзал движется с ускорением, хотя явных взаимодействий, приводящих к изменению скорости вокзала не заметно.

Поэтому закону инерции Г.Галилея ^[3] следует дать иную интерпретацию: существуют такие системы отсчета, в которых тело движется равномерно, при отсутствии взаимодействия с другими телами. Такие системы отсчета называются инерциальными.

Пусть некоторое тело А движется равномерно и прямолинейно относительно некоторой системы отсчета XOY. В любой другой системе отсчета, которая движется относительно XOY равномерно, движение тела А будет равномерным (но, конечно, с другой скоростью). Следовательно, любая система отсчета, которая движется равномерно относительно какой-нибудь инерциальной системы отсчета, сама является инерциальной.

5) Второй закон Ньютона — дифференциальный закон механического движения, описывающий зависимость ускорения тела от равнодействующей всех приложенных к телу сил и массы тела. Один из трёх законов Ньютона.

Объектом, о котором идёт речь во втором законе Ньютона, является материальная точка, обладающая неотъемлемым свойством — инертностью, величина которой характеризуется массой. В классической (ньютоновской) механике масса материальной точки полагается постоянной во времени и не зависящей от каких-либо особенностей её движения и взаимодействия с другими телами

Второй закон Ньютона в его наиболее распространённой формулировке утверждает: в инерциальных системах ускорение, приобретаемое материальной точкой, прямо пропорционально вызывающей его силе, совпадает с ней по направлению и обратно пропорционально массе материальной точки.

В приведённой формулировке второй закон Ньютона справедлив только для скоростей, много меньших скорости света, и в инерциальных системах отсчёта.

Сила трения покоя - это сила, которая мешает сдвинуть тело с места. Причина возникновения трения в том, что любые поверхности имеют неровности, которые зацепляются друг за друга. Если же поверхности отшлифованы, то причиной трения являются силы молекулярного взаимодействия. Когда тело движется по горизонтальной поверхности, сила трения направлена против движения и прямо пропорциональна силе тяжести: F = μmg Сила трения скольжения - это сила сопротивления при скольжении одного тела по поверхности другого. Сила трения качения - это сила сопротивления при качении одного тела по поверхности другого; она значительно меньше силы трения скольжения. Если трение полезно, его усиливают; если вредно - уменьшают. Сила тяжести - это сила, с которой тело притягивается к Земле вследствие Всемирного тяготения. Все тела во Вселенной притягиваются друг к другу, причем, чем больше их массы и чем ближе они расположены, тем притяжение сильнее. Чтобы вычислить силу тяжести, следует массу тела умножить на коэффициент, обозначаемый буквой g, приближенно равный 9,8Н/кг. Таким образом, сила тяжести рассчитывается по формуле F = mg Вес тела - это сила, с которой тело давит на опору или растягивает подвес из-за притяжения к Земле. Если тело не имеет ни опоры, ни подвеса, то тело не имеет и веса – оно находится в состоянии невесомости.

6) Импульс (Количество движения) — векторная физическая величина, характеризующая меру механического движения тела. В классической механике импульс тела равен произведению массы m этой точки на её скорость v, направление импульса совпадает с направлением вектора скорости: Закон сохранения импульса утверждает, что сумма импульсов всех тел (или частиц) замкнутой системы есть величина постоянная.., при движении в пустом пространстве импульс сохраняется во времени, а при наличии взаимодействия скорость его изменения определяется суммой приложенных сил. находят применение при создании современной ракетно-космической техники. Движение с помощью реактивной струи по закону сохранения импульса лежит в основе гидрореактивного двигателя.

7) Как известно, законы Ньютона выполняются только в инерциальных системах отсчета. Системы отсчета, которые движутся относительно инерциальной системы с ускорением, называются неинерциальными. В неинерциальных системах законы Ньютона, вообще говоря, уже применять нельзя. Однако законы динамики можно применять и для них, если кроме сил, которые обусловленны воздействием тел друг на друга, ввести в рассмотрение понятие силы особого рода - так называемую силу инерции. При учете сил инерции второй закон Ньютона будет справедлив для любой системы отсчета: произведение массы тела на ускорение в рассматриваемой системе отсчета равно сумме всех сил, действующих на данное тело (учитывая и силы инерции). При этом силы инерции F_in должны быть такими, чтобы вместе с силами F, обусловленными воздействием тел друг на друга, они сообщали телу ускорение а', каким оно обладает в неинерциальных системах отсчета, т. е. (1) Так как F=ma (a - ускорение тела в инерциальной системе отсчета), то Силы инерции обусловлены ускоренным движением системы отсчета относительно измеряемой системы, поэтому в общем случае следует учитывать следующие случаи возниконовения этих сил: 1) силы инерции при ускоренном поступательном движении системы отсчета; 2) силы инерции, которые действуют на тело, покоящееся во вращающейся системе отсчета; 3) силы инерции, которые действуют на тело, движущееся во вращающейся системе отсчета. Рассмотрим эти случаи. Силы инерции при ускоренном поступательном движении системы отсчета. На тележке к штативу на нити подвешен шарик массой m (рис. 1). Пока тележка покоится или движется прямолинейно и равномерно, нить, которая удерживает шарик, занимает вертикальное положение и сила тяжести Р уравновешивается силой реакции (натяжения) нити Т.

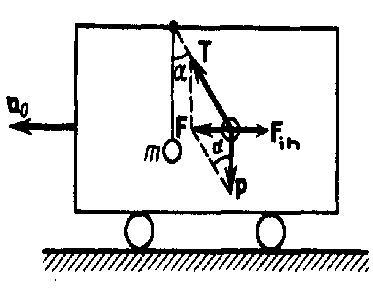
Рис.1

Если тележку привести в поступательное движение с ускорением а₀, то нить будет отклоняться от вертикали в сторону, обратную движению, до такого угла α, пока результирующая сила F=P+T не даст ускорение шарика, равное а₀. Значит, результирующая сила F направлена в сторону ускорения тележки а₀ и для установившегося движения шарика (теперь шарик движется вместе с тележкой с ускорением а₀) равна F=mgtgα=ma₀, откуда т. е. угол отклонения нити от вертикали тем больше, чем больше ускорение тележки. В системе отсчета, которая связана с ускоренно движущейся тележкой, шарик покоится, что возможно, если сила F уравновешивается равной и противоположно направленной ей силой F_in, которая является ничем иным, как силой инерции, так как на шарик никакие другие силы не действуют. Таким образом, (2) Проявление сил инерции при поступательном движении мы можем видеть в повседневных явлениях. Если поезд набирает скорость, то пассажир, сидящий при этом по ходу поезда, прижимается к спинке сиденья под действием силы инерции. Наоборот, при торможении поезда пассажир отклоняется от спинки сиденья, т.к. сила инерции направлена в противоположную сторону. Особенно силы инерции заметны при внезапном торможении поезда. Эти силы проявляются в перегрузках, возникающие при запуске и торможении космических кораблей. Силы инерции, действующие на тело, покоящееся во вращающейся системе отсчета. Пусть диск равномерно вращается с угловой скоростью ω (ω=const) вокруг перпендикулярной ему оси, которая проходит через его центр. На диске установлены маятники, на разных расстояниях от оси вращения и на нитях висят шарики массой m. Когда диск начнет вращаться, шарики отклоняются от вертикали на некоторый угол (рис. 2).

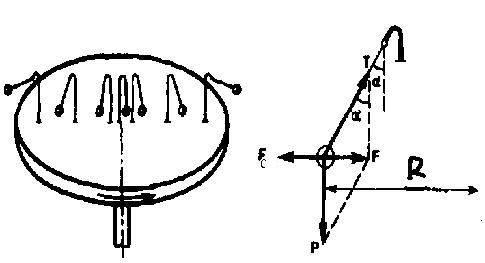
Рис.2

В инерциальной системе отсчета, которая связана, например, с помещением, где установлен диск, происходит равномерное вращение шарика по окружности радиусом R (расстояние от центра вращающегося шарика до оси вращения). Значит, на него действует сила, равная F=mω²R и которая направлена перпендикулярно оси вращения диска. Она является равнодействующей силы тяжести Р и силы реакции (натяжения) нити Т: F=P+T. Когда движение шарика установится, то F=mgtgα=mω²R, откуда т. е. углы отклонения нитей маятников будут тем больше, чем больше угловая скорость вращения &omega и чем больше расстояние R от центра шарика до оси вращения диска;. Относительно системы отсчета, которая связана с вращающимся диском, шарик покоится, что возможно, если сила F уравновешивается равной и противоположно направленной ей силой F_с, являющаяся ничем иным, как силой инерции, так как никакие другие силы на шарик не действуют. Сила F_c, называемая центробежной силой инерции, направлена по горизонтали от оси вращения диска и равна (3) На практике действие центробежных сил инерции испытывают, например, пассажиры в движущемся автобусе на поворотах, летчики при выполнении фигур высшего пилотажа; центробежные силы инерции используются во всех центробежных механизмах: насосах, сепараторах и т. д., где они достигают очень больших значений. При проектировании быстро вращающихся деталей машин (винтов самолетов, роторов и т. д.) используются специальные механизмы для уравновешивания центробежных сил инерции. Из формулы (3) следует, что центробежная сила инерции, которая действует на тела во вращающихся системах отсчета и которая направлена в сторону радиуса от оси вращения, зависит от угловой скорости вращения ω системы отсчета и радиуса R, но при этом не зависит от скорости тела относительно вращающихся систем отсчета. Значит, центробежная сила инерции действует во вращающихся системах отсчета на все тела, которые удалены от оси вращения на конечное расстояние, при этом не имеет значения, покоятся ли они в этой системе отсчета (как мы предполагали до сих пор) или движутся относительно нее с некоторой скоростью. Силы инерции, действующие на тело, движущееся во вращающейся системе отсчета. Пусть шарик массой m движется с постоянной скоростью ν' вдоль радиуса равномерно вращающегося диска (ν'=const, ω=const, ν перпендикулярно ω). Если диск не начал вращаться, то шарик, движется по радиальной прямой и попадает в точку А, если же диск привести во вращение в направлении, которое указанно стрелкой, то шарик покатится по кривой OВ (рис. 3а), причем его скорость ν' относительно диска сменит свое направление. Это возможно лишь в случае, если на шарик действует сила, которая перпендикулярна скорости ν'.

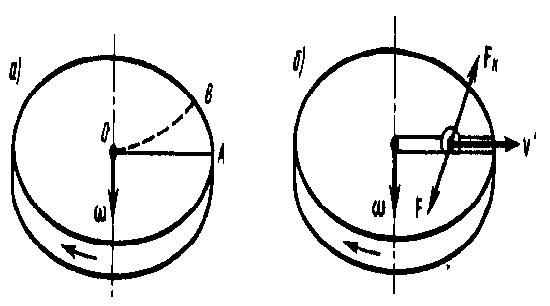
Рис.3

Чтобы заставить шарик катиться по вращающемуся диску вдоль радиуса, будем использовать жестко укрепленный вдоль радиуса диска стержень, на котором шарик движется без трения прямолинейно равномерно со скоростью ν' (рис. 3б). При отклонении шарика стержень действует на него с некоторой силой F. Во вращающейся системы отсчета, т.е. относительно диска, шарик движется прямолинейно и раномерно, что объясняется тем, что сила F уравновешивается приложенной к шарику силой инерции F_k, которая перпендикулярной скорости ν'. Эта сила называется кориолисовой силой инерции. Можно показать, что сила Кориолиса Вектор F_k перпендикулярен векторам скорости v' тела и угловой скорости вращения системы отсчета в соответствии с правилом правого винта. Сила Кориолиса действует только на тела, которые движутся относительно вращающейся системы отсчета, чаще всего рассматривается случай относительно Земли. Действием этих сил объясняется ряд наблюдаемых на Земле явлений. Так, если тело движется в северном полушарии на север (рис. 4), то действующая на него сила Кориолиса, как это следует из выражения (4), будет направлена вправо по отношению к направлению движения, т. е. тело несколько отклонится на восток. Если тело движется на юг, то сила Кориолиса также действует вправо, если смотреть по направлению движения, т. е. тело отклонится на запад. Поэтому в северном полушарии наблюдается более сильное подмывание правых берегов рек; правые рельсы железнодорожных путей по движению изнашиваются быстрее, чем левые, и т. д. Также можно показать, что в южном полушарии сила Кориолиса, которая действует на движущиеся тела, направлена влево по отношению к направлению движения.

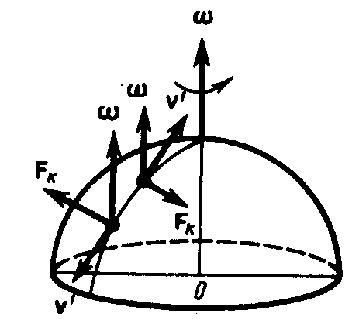Благодаря действию силы Кориолиса падающие на поверхность Земли предметы отклоняются к востоку (на широте 60° это отклонение должно составлять 1 см при падении с высоты 100 м). С силой Кориолиса связано движение маятника Фуко, которое явилось в свое время одним из доказательств вращения Земли. Если бы силы Кориолиса не было, то тогда плоскость колебаний качающегося вблизи поверхности Земли маятника оставалась бы неизменной (относительно Земли). Действие же данной силы приводит к вращению плоскости колебаний вокруг вертикального направления. Раскрывая содержание F_in в формуле (1), получим основной закон динамики для неинерциальных систем отсчета: где силы инерции задаются формулами (2) - (4). Еще раз подчеркнем, что силы инерции вызываются не взаимодействием тел, а ускоренным движением системы отсчета. По этой причине они не подчиняются третьему закону Ньютона, так как если на тело действует сила инерции, то не существует силы, противодействующей ей и приложенной к данному телу. Два основных положения механики, по которым ускорение всегда вызывается силой, а сила всегда обусловлена взаимодействием между телами, в системах отсчета, движущихся с ускорением, одновременно не выполняются. Для любого из тел, которые находятся в неинерциальной системе отсчета, силы инерции являются внешними; Значит, здесь нет замкнутых систем, т.е. в неинерциальных системах отсчета не выполняются также и законы сохранения импульса, энергии и момента импульса. Значит, силы инерции действуют только в неинерциальных системах отсчета. В инерциальных системах отсчета таких сил не существует.