1,2) Кинематика материальной точки. Координатная, векторная и траекторная формы описания движения. Перемещение, скорость и ускорение материальной точки.

Мгновенное положение материальной точки (Р) в пространстве можно описать при помощи радиуса-вектора этой точки, начало которого связано с началом координат (рис. 1.1). Радиус- вектор в данный момент времени является функцией координат (x, y, z). Разложим вектор на сумму векторов, направленных по осям координат :

,

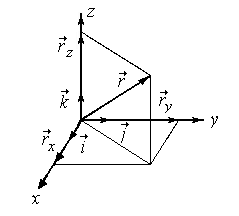
где (x, y, z) – проекции вектора на координатные оси (координаты точки), – орты соответствующих осей.

В векторной форме радиус-вектор записывается:

,

длина вектора (модуль вектора):

.

При движении материальной точки конец ее радиуса-вектора описывает в пространстве некоторую линию (годограф), называемую траекторией. Форма траектории определяет характер движения – прямолинейное или криволинейное. Длина траектории называется длиной пути ( ). Путь – скалярная функция времени и всегда положительная величина.

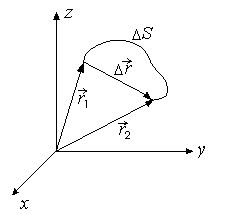
Разность радиусов-векторов, определяющих два положения материальной точки в моменты времени t₁ и t₂, называется вектором перемещения (рис. 1.2).

При прямолинейном движении модуль вектора перемещения равен длине пути . В общем случае криволинейного движения это равенство возможно лишь для бесконечно малого отрезка времени

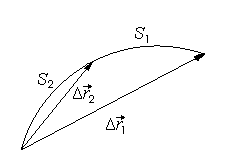
Запишем вектор перемещения и модуль вектора перемещения в координатной форме.

Так как:

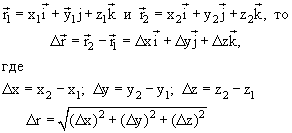
Пусть материальная точка движется по криволинейной траектории из точки А, положение которой задается радиусом-вектором

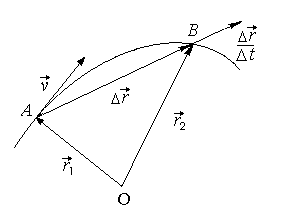Через некоторое время она будет находиться в точке В, радиус-вектор которой . Перемещение точки равно вектору  , пройденный путь  равен длине дуги AB.  Вектором средней скорости движения материальной точки называется отношение перемещения  ко времени , за которое это перемещение произошло

Средней путевой скоростью называется отношение:

Уменьшим время наблюдения, при этом перемещение также уменьшится. Отношение при стремится к определенному пределу, называемому вектором мгновенной скорости. Мгновенная скорость – вектор, направленный по касательной к кривой в точке А, так как, по определению, касательная – это предельное положение секущей при бесконечно малом перемещении.

Единица измерения скорости – [м/с].

Вектор скорости – первая производная радиуса–вектора по времени. Модуль вектора скорости – первая производная пути по времени. Так как

то т.  е.

Запишем вектор скорости в координатной форме ,

где –  проекции вектора скорости на соответствующие оси координат

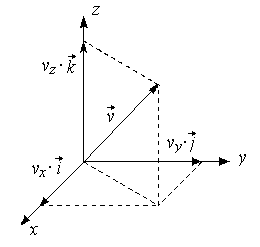Модуль вектора скорости равен: .

В случае, если тело за сколь угодно малые равные промежутки времени проходит одинаковые отрезки пути , то тело движется равномерно , с постоянной скоростью. При этом мгновенная скорость в разные моменты времени по модулю остается постоянной.

Так, движение точки по окружности с постоянной по величине скоростью является равномерным, но криволинейным.