15. Расчет осадки фундамента по методу эквивалентного слоя

Во многих случаях осадки фундаментов можно рассчитывать простым методом эквивалентного слоя, разработанным Н. А. Цытовичем. Основные допущения этого метода при мощном слое однородного грунта:

грунт однороден в пределах полупространства; грунт представляет собой линейно деформируемое тело, т. е, деформации его пропорциональны напряжениям; деформации грунта в пределах полупространства принимаются по теории упругости.

Из теории упругости известно, что осадка поверхности линейно деформируемого полупространства может быть найдена по формуле Шлейхера:

где — коэффициент осадки, зависящий от формы площади загружения, жесткости фундамента и места расположения точки поверхности грунта, в которой определяется осадка.

Согласно выражению (2.13),

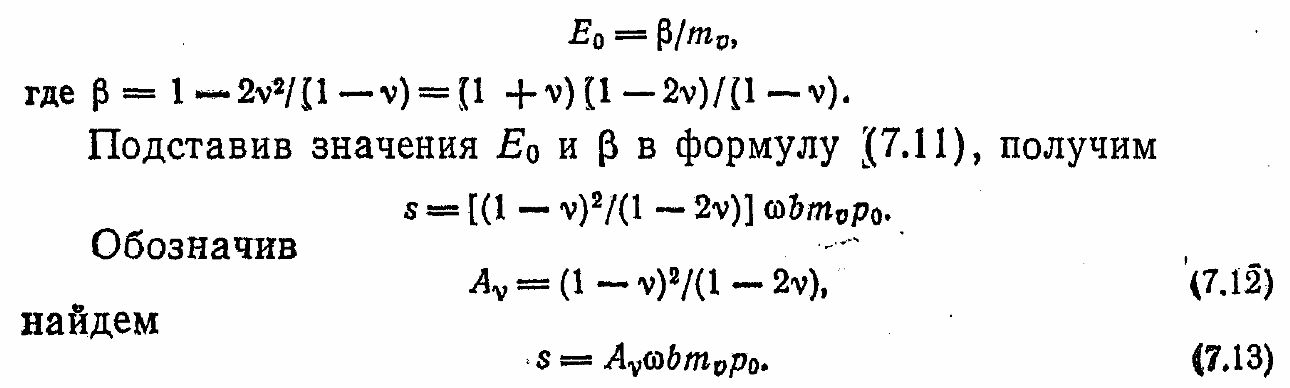
где h — толщина слоя грунта, к поверхности которого приложена сплошная нагрузка интенсивностью р.

Поскольку р в формуле (7.1) имеет то же значение, что и р_о в формуле (7.13), произведение A_vωb можно рассматривать как толщину эквивалентного слоя h_e , осадка поверхности которого при сплошной нагрузке равна осадке фундамента:

h_e= A_vωb (7.14)

С учетом этого получим окончательное выражение для определения осадки фундамента

s= h_em_vp₀ (7.16)

Таким образом, определив по (7.14) толщину эквивалент­ного слоя h_e , по формуле (7.15) легко найти осадку фундамента, точно соответствующую осадке поверхности бесконечного полупространства под действием местной нагрузки, вычисляемой по (7.11). Произведение A_vω, называемое коэффициентом эквивалентного слоя для абсолютно жестких фундаментов, приведено в табл. 7.2 (ее нет, и не ищите в шпорах).

21 Давление грунтов на подпорные стены с учетом нагрузки на горизонтальной поверхности засыпки

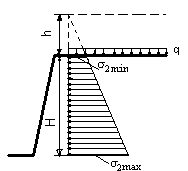
В случае действия на поверхность грунта сплошной равномерно распределенной нагрузки q, Н/м², распределенную нагрузку заменяем эквивалентным слоем грунта создающим такое же давление на засыпку. Величина условного слоя

определяется исходя из величины нагрузки и исходного веса грунта.

Приведенная высота слоя грунта h=q/g

Продолжаем заднюю грань стенки до пересечения с новой линией засыпки и строим общую треугольную эпюру давлений.

s_2min=g*h*tg²(45-y/2)

s_2max=g*(h+H)*tg²(45-y/2)

На подпорную стенку будет действовать только трапецеидальная заштрихованная часть эпюры давления. Тогда Е_а=g/2(H²+2h*H)*tg²(45-y/2)

Где Е_а –активное давление

Е_n =g/2(H²+2h*H)*tg²(45+y/2)

Е_n –пассивное давление

24 Модуль деформации грунтов. Методы определения модуля деформации грунтов.

Модуль общей деформации грунта используется в качестве деформационного показателя и характеризует упругие и остаточные деформации (см. рис. 5.5). Модуль общей деформации является важной характеристикой, используемой для расчета оснований и сооружений по деформациям. Модуль общей деформации определяется в полевых и лабораторных условиях. Наиболее распространен способ проведения компрессионных испытаний с последующей их обработкой. В этом случае модуль общей деформации

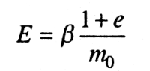(5.24)

где е — коэффициент пористости грунта в природном состоянии;

m₀ - коэффициент сжимаемости (уплотнения) МП -1;

β— безразмерный коэффициент, определяемый в зависимости от коэффициента поперечного расширения v по формуле

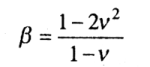(5.25)

или от коэффициента бокового давления ξ

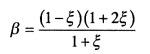(5.26)

Для крупнообломочных грунтов β = 0,8; песков и супесей - 0,74, суглинков - 0,62 и глин - 0,93.

Значение модуля деформации грунта, найденное с использованием компрессионных кривых, отличается от действительного, так как при отборе образцов грунта все же происходит какое-то нарушение его природной структуры. Поэтому для определения модуля деформации используют полевой метод испытания грунта статической нагрузкой. По результатам испытаний строится график зависимости осадки от нагрузки (рис. 5.10).

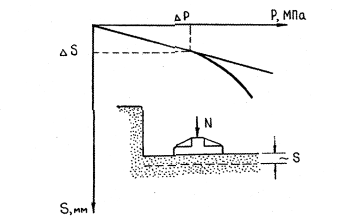
Рис. 5.10. График зависимости осадки штампа от давления