13. Методы «угловых точек» определения напряжений в массиве грунта. Использование этого метода в расчетах оснований фундаментов.

Если закон распределения давления по поверхности изотропного линейно деформируемого полупространства известен, то элементарное суммирование можно заменить интегрированием.

– при разворачивании этого интеграла получается очень громоздкая формула, поэтому при равномерно распределенном давлении после интегрирования по прямоугольной площади загружения значения для точек, расположенных под центром прямоугольной площади загружения (рис. 4.9,а), получим:

Где – принимается по таблице 4.2; Р – равномерно распределенное давление.

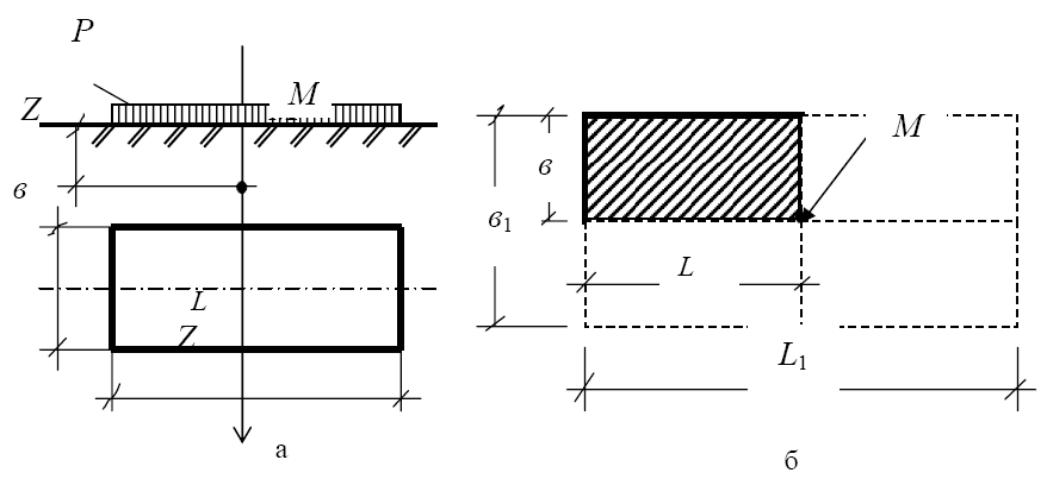
Рис. 4.9. Расчетные схемы к определению напряжений Z σ при действии местного равномерно распределенного давления: а – для точек, расположенных под центром прямоугольной площади загружения; б – под угловыми точками прямоугольной площади загружения

При нахождении Z σ под угловыми точками прямоугольной площади загружения (например, под точкой М) (рис. 4.9, б), значения (а не 2·Z, т. к. в1=2в), также можно принимать по таблице 4.2.

Напряжение под угловыми точками определяют по формуле

Для определения вертикального напряжения Z σ в любой точке полупространства можно воспользоваться выражением Z σ = 0,25 ⋅α 'Р . Действительно, если проекция рассматриваемой точки М' на горизонтальную поверхность полупространства (точка М) располагается в пределах площади загружения (рис. 4.10, а), то эту площадь можно разбить на четыре прямоугольника (I – Meaf, II – Mfbg, III – Mgch, IV – Mhde) так, чтобы точка М была угловой точкой каждого из них.

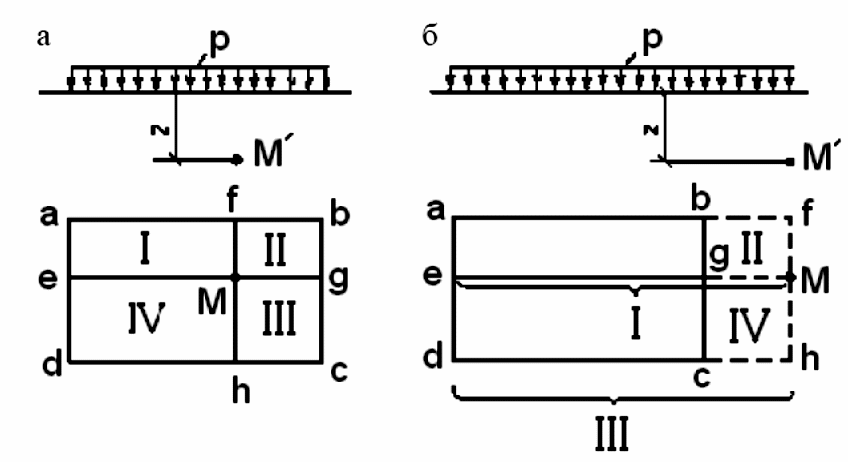
Рис. 4.10. Расчетные схемы к определению напряжений Z σ при действии местного равномерно распределенного давления: а – для точек, расположенных внутри прямоугольной площади загружения; б – под точками, расположенными вне прямоугольной площади загружения

Тогда напряжение Z σ найдем суммированием напряжений под угловыми точками четырех площадей загружения:

где α₁’, α₂’,α₃’,α₄’ – коэффициенты, принимаемые по таблице в зависимости от отношения сторон площадей загружения I, II, III, IV и отношения Z (глубины расположения точки М') к ширине каждой из этих площадей.

Когда проекция точки М' на горизонтальную поверхность полупространства (точка М) располагается вне пределов площади загружения (рис. 4.6, б), точку М аналогично можно представить как угловую точку фиктивных площадей загружения I, II, III, IV. При этом в пределах площадей II и IV фиктивная нагрузка прикладывается в обратном направлении.

Напряжение определяется по выражению

Обобщая формулы, можно дать следующее определение методу угловых точек: напряжение в произвольной точке от нагрузки, распределенной по прямоугольной площади, равно алгебраической сумме напряжений в угловых точках прямоугольников, для которых рассматриваемая точка является угловой, при этом алгебраическая сумма площадей этих прямоугольников с учетом знаков в формуле суммирования напряжений должна совпадать с фактической площадью нагрузки. Так, пользуясь методом угловых точек, можно найти напряжение σ_z в любой точке полупространства, к поверхности которого приложена равномерно распределенная нагрузка в пределах прямоугольной площади.