11. Распределение вертикальных напряжений в линейно-деформируемой среде при действии на ее поверхности сосредоточенной силы (задачи Буссинеска)

Определение напряжений Z σ в массиве грунта при действии единичной вертикальной силы N, приложенной к границе грунтового основания.

Решение задачи Буссинеска.

Основано на следующих гипотезах (впоследствии подтвержденных точными решениями): а) нормальные напряжения на площадках, касательных к сферической поверхности с центром в точке приложения силы, являются главными напряжениями. По этой причине касательные напряжения на указанных площадках отсутствуют; б) нормальные напряжения, лежащие в вертикальной плоскости, на площадках, нормальных к сферической поверхности с центром в точке приложения силы, равны нулю; в) нормальные напряжения на площадках, касательных к сферической поверхности с центром в точке приложения силы, прямо пропорциональны косинусу угла видимости и обратно пропорциональны квадрату радиуса сферы. Под углом видимости понимается угол между радиусом сферы, проведенным в центр площадки, и центральной вертикальной осью сферы.

Постулированные гипотезы позволяют получить замкнутые аналитические решения о распределении напряжений в полупространстве от действия вертикальной силы на его границе, основанные исключительно на уравнениях равновесия. Решение задачи поясняется графическими построениями на рис. 4.5, на котором представлены вертикальный разрез полупространства и его сечения горизонтальными плоскостями.

Начало прямоугольной декартовой системы координат разместим в точке приложения вертикальной силы Р на границе полупространства. Ось z направим по вертикали вниз, ось x – по горизонтали вправо, а ось y – перпендикулярно плоскости чертежа. Относительно начала осей координат построена полусфера радиусом R, пересечение которой с вертикальной плоскостью, проходящей через центральную ось, образует полуокружность такого же радиуса. В сечении полусферы горизонтальной плоскостью на глубине z образуется окружность радиусом r. Угол видимости радиуса r на вертикальном разрезе обозначим β. В сечении полусферы горизонтальной плоскостью на глубине z – dz образуется окружность радиусом r + dr с углом видимости на вертикальном разрезе β + dβ. Рассмотрим равновесие сферического кольца, выделенного из полусферы двумя горизонтальными плоскостями на глубине z и z – dz. С учетом того, что длина образующей сферического кольца равна R·dβ, площадь его поверхности определится формулой: S = 2⋅π⋅r⋅R⋅dβ. На поверхности сферического кольца действуют нормальные напряжения σR, а касательные напряжения, в соответствии с гипотезой а), отсутствуют.

Практический интерес представляют напряжения на горизонтальной площадке, наклоненной к площадке, на которой действуют напряжения σR, под углом β. В соответствии с гипотезой б) главный вектор напряжений на горизонтальной площадке σ′R совпадает по направлению с вектором напряжения σR, а его модуль равен σ′R = σR ⋅ cosβ. Проекции главного вектора напряжений σ′R на координатные оси являются компонентами тензора напряжений на горизонтальной площадке. Поскольку главный вектор напряжений σ′R совпадает по направлению с радиусом вектором R, направляющие косинусы вектора напряжений определяются формулами:

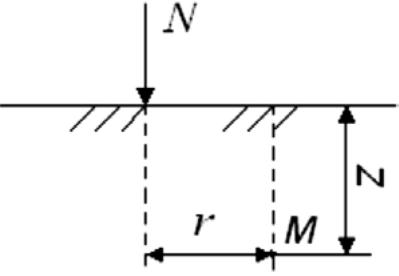
В дальнейшем для практических расчетов расчетную схему задачи приводят к более простому виду (рис.4.6). Вертикальные напряжения в расчетной точке М определяют по формуле

Коэффициент К, зависящий от безразмерного параметра r/z, приводится в справочных данных.

Z – глубина точки;

r – расстояние от точки до линии действия силы;

М – рассматриваемая точка;

N – сосредоточенная вертикальная сила.