4.2.Область значення функції

Область значення функції - це множина значень, яких функція набуває для всіх значень аргументу з області визначення.

Область визначення функції може складатись з окремих точок, однієї точки, одного чи кількох інтервалів, з множини всіх дійсних чисел.

Для відшукання області значень функції у=f(х) потрібно знайти всі значення у для яких рівняння y=f(х) має дійсні розв'язки. Якщо загальний розв'язок рівняння у=f(х) можна записати у вигляді х= E(у), то для відшукання області значень функції f потрібно знайти множину та у, для яких вираз E (у) має смисл.

4.3. Задачі на знаходження овф і озф

Завдання Розв’язання

Приклад 1. Знайти область визначення функції  .

Розв’язання.

Для того, щоб знайти область визначення функції  , розв’яжемо нерівність          ;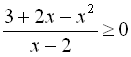

    

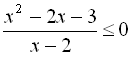
Рис. 4.1

Тоді      (Рис. 4.1).

Відповідь:      .

Приклад 2. Знайти область визначення функції y = (x³ – 6x² + 5x)^1/2.

Розв’язання.

Вираз має смисл, якщо підкореневий вираз невід’ємний, тобто

x³ – 6x² + 5x ≥ 0,

x(x² – 6x + 5) ≥ 0,

x (x – 5) (x – 1) ≥ 0.

Розв’яжемо дану нерівність методом інтервалів (рис. 4.2).

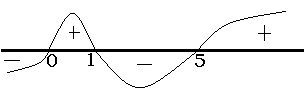
Р ис. 4.2

О тже, х є [0;1] [5;+oo].

Відповідь: [0;1] [5;+oo].

Приклад 3. Знайти область визначення функції y = (64 – 4^x)^1/2.

Розв’язання.

Вираз має смисл, якщо підкореневий вираз невід’ємний, тобто

(64 – 4^x) ≥ 0,

64 ≥ 4^x,

4³ ≥ 4^x.

Оскільки 4 > 1, то нерівність 4³ ≥ 4^x рівносильна нерівності 3 ≥ x, звідки x ≤ 3.

Відповідь: [-oo;3].

Приклад 4. Знайти область визначення і множину значень функцій:

а)  ; б)  .

Розв’язання.

а)  . Оскільки область зміни х не вказано, природно областю визначення функції вважати множину всіх значень змінної х, при яких ця відповідність має сенс. Отже, у даному випадку    .

Легко збагнути, що    . Знайдемо значення функції при декількох значеннях аргументу:  ,  ,

.

б)  . Тут      . Для знаходження області значень   виразимо х через  :  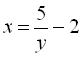. Звідси видно, що      . Знайдемо значення функції при деяких значеннях х:  ;  ;  .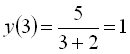

Приклад 5. Знайти область значення функції y = 2^{x + 1} – 2.

Розв’язання.

Оскільки графік показникової функції y = 2^x лежить над віссю абсцис, то 2^x > 0. Тому 2^{x + 1} – 2 > -2, тобто y > -2.

Відповідь: (-2;+оо).

Приклад 6. Знайти область значення функції y = (x² – x – 2)^1/2.

Розв’язання.

Перетворимо функцію y = (x² – x – 2)^1/2:

y² = x² – x – 2,

y² = (x – 0.5)² – 9/4,

(x – 0.5)² = y² + 9/4,

y² + 9/4 ≥ 0,

y ≥ 0.

Відповідь: [0;+oo].

4.4. Парність і непарність функції

Числова множина X називається симетричною, якщо для будь-якого хєХ число -хєХ.

Функція f, визначена на симетричній множині X, називається парною, якщо для будь-якого хєХ виконується рівністьf(-х)=f(х).

Функція f, визначена на симетричній множині X, називається непарною, якщо для будь-якого xєХ виконується рівність f(-х)=-f(х).

З означень парної і непарної функції випливає, що втрачає смисл розгляд на парність чи непарність функції, визначеної на несиметричній площині. Умова симетричності області визначення функції є необхідною для того, щоб функція могла бути парною чи непарною. Але вона не є достатньою.

Функції, що не є а ні парними, а ні непарними, називають функціями, що не мають властивостей парності.

Довільну функцію f(х), визначену на симетричній множині, можна подати у вигляді суми непарної функції:

F(x)=(f(x) + f(-x))/2 + (f(х)-f(-х))/2, де перший доданок - парна функція, а другий - непарна, і таке поєднання – єдине.

Рис. 4.3. f (x) = x – непарна функція.

Рис. 4.4. f (x) = x ^{3 -} непарна функція.

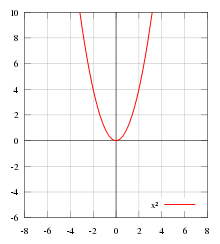
Рис. 4.5. f (x) = x ² - парна функція.

Рис. 4.6. f (x) = x ³ + 1 – ні парна, ні непарна функція.

Приклад № 1. Дослідити на парність функцію x ² / (4 · x ² - 1).

Розв’язання.

Підставляємо в дану функцію - x замість x. Ми побачите, що знак функції не зміниться, оскільки аргумент в обох випадках присутній в парному ступеня, що нейтралізує негативний знак. Отже, досліджувана функція є парною.     

Приклад № 2. Перевірити функцію на парність і непарність: f =-x ² + 5 · x.

Розв’язання.  Як і в попередньому прикладі, підставимо -x замість x: f (-x) =-x ² - 5 · x. Очевидно, що f (x) ≠ f (-x) і f (-x) ≠-f (x), отже, функція не має властивості ні парності, ні непарності. Така функція називається функцією загального вигляду.     

Дослідити функцію на парність і непарність можна також наочним чином при побудові графіка або знаходженні області визначення функції. У першому прикладі областю визначення є безліч x ∈ (- ∞; 1/2) ∪ (1/2; + ∞). Графік функції симетричний відносно осі Oy, значить, функція парна.     

У курсі математики спочатку вивчають властивості елементарних функцій, а потім отримані знання переносять на дослідження більш складних функцій.

Приклад № 3. Перевірити функцію на парність і непарність: f(x) = x⁵cos 3x.

Розв’язання.  Функція визначена на множені (-оо; +оо), тобто її область визначення симетрична відносно початку координат.

Крім того, f (-x) = (-x)⁵cos 3(-x) = -x⁵cos 3x = -f(x) для будь-якого x є R.

Отже, функція f(x) = x⁵cos 3x – непарна.