Для побудови графіка функції треба піддати графік функції f розтязі з коефіцієнтом k вздовж осі абсцис.

Приклад 5. Побудова графіків функцій і показано на рисунках 5.17 і 5.18.

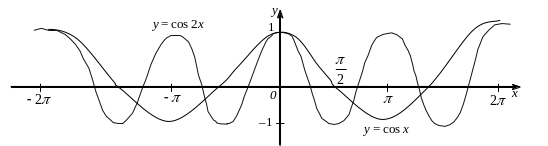
Рис. 5.17

Рис. 5.18

Висновки

Матеріальна єдність світу виявляється у взаємозв'язку і взаємо обумовленості різних явищ і процесів, що відбувається в природі. Розглядаючи їх, доводиться вираховувати залежності одних змінних від інших. Наприклад, залежність шляху від часу, залежність кількості купленого товару на певну суму від ціни, залежність між площею круга і його радіусом. Необхідність вивчення на практиці залежностей між змінними різної природи привела до поняття функції в математиці. Всі функції, які ми вивчаємо в школі, застосовуються на практиці. Наприклад, графік у=ах³ використовують проектувальники залізниць та автомобільних шляхів, якщо треба зробити плавний перехід від прямолінійних до криволінійних ділянок шляху. На практиці також використовують функцію у=ах^1/2 .  Зокрема, за допомогою цієї функції вражають залежність періоду Т малих коливань математичного маятника від його довжини І:Т=2П (1/g)^1/2, де g - прискорення сили тяжіння.

Під час виконання даної роботи я закріпив і поглибив теоретичні знання з основних проблем цієї навчальної дисципліни. З’ясував свій рівень теоретичної підготовки, вміння самостійно і творчо працювати з науковою літературою, правильно аналізувати, тлумачити і застосовувати вивчений матеріал.

Використана література

1. В'.А.Вишенський, А.Я. Дороговцсв ,',Вибрані питання елементарної математики".

2. Т.Н.Ничипорук „Елементарні функції, їх властивості і графіки".

3. З.І.Слєпкань, О.С.Дубинчук „Функції, їхнє значення та застосування".

4. В.П.Борисенко „Построение касательньїх" (научно - популярний физико-математический журнал „Квант"№9, 1981.

5. Українська радянська енциклопедія. В 12-ти томах / За ред. М. Бажана. — 2-ге вид. — К.: Гол. редакція УРЕ, 1974-1985.

6. Периодическая функция (Большая советская энциклопедия).

7. Коломогоров А. Н., Фомин С. В. Элементы теории функций и функционального анализа. — М.: Наука, 1989. — 624 с.

8. Функция. Математический энциклопедический словарь. — Гл. ред. Ю. В. Прохоров. — М.: «Большая российская энциклопедия», 1995.

9. Клейн Ф. Общее понятие функции. В кн.: Элементарная математика с точки зрения высшей. Т. 1. М.—Л., 1933.

10. А. Н. Колмогоров, С. В. Фомин. Глава 1. Элементы теории множеств // Элементы теории функций и функционального анализа. — 3-е изд. — М.: Наука, 1972. — С. 14—18. — 256 с.

11. В. А. Зорич. Глава I. Некоторые общематематические понятия и обозначения. § 3. Фунция // Математический анализ, часть I. — М.: Наука, 1981. — С. 23—36. — 544 с.

12. Г. Е. Шилов. Глава 2. Элементы теории множеств. § 2.8. Общее понятие функции. График // Математический анализ (функции одного переменного). — М.: Наука, 1969. — С. 65—69. — 528 с.

13. А. Н. Колмогоров. «Что такое функция» // «Квант». — М.: «Наука», 1970. — В. 1. — С. 27—36. — ISSN 0130-2221.

14. График // Энциклопедический словарь Брокгауза и Ефрона: В 86 томах

(82 т. и 4 доп.). — СПб., 1890—1907.

15. Мерзляк А. Г., Полонський В. Б., Якір М. С. Алгебра: Підруч. для 8 кл. з поглибл. вивч. математики. – Х.: Гімназія, 2008. – 368 с.

16. Мерзляк А. Г., Полонський В. Б., Якір М. С. Алгебра: Підруч. для 9 кл. з поглибл. вивч. математики. – Х.: Гімназія, 2009. – 384 с.

17. Нелін Є. П. Алгебра і початки аналізу : Підруч. для 10 кл. загальноосвіт. навчальн. закладів: профільн. рівень. – Х.: Гімназія, 2010. – 416 с.