21. Первый закон термодинамики. Закон распределения кинетической энергии молекул по степеням свободы. Внутренняя энергия идеального газа. Работа расширения газа. Первый закон термодинамики.

Закон распределения кинетической энергии молекул по степеням свободы Молекулы можно рассматривать как системы материальных точек (атомов) совершающих как поступательное, так и вращательное движения. При исследовании движения тела необходимо знать его положение относительно выбранной системы координат. Для этого вводится понятие о степенях свободы тела. Число независимых координат, которые полностью определяют положение тела в пространстве, называется числом степеней свободы тела. Закон равномерного распределения энергии по степеням свободы молекул можно сформулировать следующим образом: статистически в среднем на каждую степень свободы молекул приходится одинаковая энергия. Поступательное движение молекул характеризуется средней кинетической энергией, равной  . Так как поступательному движению соответствует 3 степени свободы, то в среднем на одну степень свободы движения молекул приходится энергия В однородном газе, молекулы которого имеют любое число степеней свободы i, каждая молекула в среднем обладает энергией движения, равной Внутренняя энергия идеального газа. В теории идеального газа потенциальная энергия взаимодействия молекул считается равной нулю. Поэтому внутренняя энергия идеального газа определяется кинетической энергией движения всех его молекул. Средняя энергия движения одной молекулы равна

Так как в одном киломоле содержится   молекул, то внутренняя энергия одного киломоля газа будет Учитывая, что   , получим Для любой массы m газа, т.е. для любого числа киломолей   внутренняя энергия Из этого выражения следует, что внутренняя энергия является однозначной функцией состояния и, следовательно, при совершении системой любого процесса, в результате которого система возвращается в исходное состояние, полное изменение внутренней энергии равно нулю. Математически это записывается в виде тождества Работа расширения идеального газа Работа над газом выполняется внешними силами при его сжатии. Работа самого газа выполняется при его расширении. Пусть газ расширяется так, что поршеньподнимается на величину dx. Тогда газ выполнит работу   (S – площадь поршня). Получим Эта величина называется элементарной работой газа. Работа при расширении газа от объема V₁ до V₂будет равна Если по одной оси отложить объем газа, по другой – его давление (плоскость P – V), то работа будет изображаться площадью под кривой P(V)  Работа расширения  зависит от того, каким образом это расширение происходит.  Значение работы расширения идеального газа зависит от условий. Наибольшая работа получится тогда, когда в процессе расширения внешнее давление все время лишь на бесконечно малую величину меньше собственного давления газа, и расширение происходит очень медленно. Первый закон термодинамики - есть закон сохранения энергии: при любых физических взаимодействиях энергия не возникает и не исчезает, а только передается от одних тел другим или превращается из одной формы в другую. Общая форма закона сохранения и превращения энергии имеет вид - изменение механической энергии системы, – изменение внутренней энергии тел системы, A –работа внешних сил, Q – количество теплоты, полученной системой. Но изучая тепловые процессы, мы будем рассматривать формулу  Согласно первому закону термодинамики, изменение внутренней энергии термодинамической системы при переходе из одного состояние в другое равно сумме работы, выполненной внешними силами, и количества теплоты, переданной системе извне –изменение внутренней энергии системы A- работа внешних сил Q – количество полученной системой теплоты.

Сформулировать первый закон термодинамики можно иначе: количество теплоты, получаемое системой извне при ее переходе из одного состояния в другое, расходуется на повышение внутренней энергии системы и на работу, которую она выполняет против внешних сил изменение внутренней энергии системы работа силой термодинамической системы Q – количество полученной системой теплоты

 Например, вы кипятите чайник с водой. Количество тепла расходуется на их нагревание (увеличивается энергия частиц, то есть внутренняя энергия системы), а затем происходит приподнимание крышки - это работа, которую выполняет система.

Внешняя работа над системой равна работе системы, но с противоположным знаком

22.Термодинамика изопроцессов. Первый закон термодинамики для изобарного, изохорного, изотермического процессов. Адиабатический процесс. Уравнение Пуассона. Первый закон термодинамики для изобарного, изохорного, изотермического процессов При изотермическом процессе температура не изменяется, значит не изменяется внутренняя энергия  Первый закон принимает вид  Все количество теплоты, которую получает газ расходуется на выполнение им работы против внешних сил. Или, если газ сжимается, при этом не изменяется температура, работу выполняют внешние силы, а газ отдает некоторое количество теплоты в окружающую среду. При изохорном процессе объем не изменяется, значит работа нулевая Первый закон термодинамики принимает вид  В этом случае   Если газ изохорно охлаждается, его внутренняя энергия уменьшается, и он отдает теплоту в окружающую среду. При изобарном процессе первый закон термодинамики имеет общий вид   Здесь справедливы формулы   Адиабатический процесс. (адиабатный) Процесс при тепловой изоляции системы от окружающей среды, то есть Q=0 Изменение внутренней энергии происходит только за счет работы внешних сил. Или совершаемая системой работа происходит за счет убыли внутренней энергии.

Практически все реальные процессы происходят с теплообменом: адиабатические процессы - это редкое исключение. Уравнение Пуассона Уравнение адиабатного процесса (уравнение Пуассона)

23.Теплоемкости идеального газа. Теплоемкость удельная, молярная и связь между ними. Удельная и молярная теплоемкости газа при постоянном объеме, постоянном давлении. Уравнение Майера.

Молярная теплоёмкость — отношение теплоёмкости к количеству вещества, теплоёмкость одного моля вещества . Это физическая величина, численно равная количеству теплоты, которое необходимо передать одному молю (данного) вещества для того, чтобы его температура изменилась на единицу.  молярная теплоёмкость измеряется в Дж/(моль·К).

Молярная теплоёмкость обычно обозначается   или  , иногда без индекса или с другим индексом (характеризующим условия процесса измерения, нумерующим подсистемы итп). На значение молярной теплоёмкости влияет температура вещества и другие термодинамические параметры. Уде́льная теплоёмкость — отношение теплоёмкости к массе, теплоёмкость единичной массы вещества (разная для различных веществ); физическая величина, численно равная количеству теплоты, которое необходимо передать единичной массе данного вещества для того, чтобы его температура изменилась на единицу. удельная теплоёмкость измеряется в  Дж/(кг·К). Удельная теплоёмкость обычно обозначается буквами c или С, часто с индексами.На значение удельной теплоёмкости влияет температура вещества и другие термодинамические параметры.

Формула расчёта удельной теплоёмкости:   , где c — удельная теплоёмкость, Q — количество теплоты, полученное веществом при нагреве (или выделившееся при охлаждении), m — масса нагреваемого (охлаждающегося) вещества, ΔT — разность конечной и начальной температур вещества. Удельная теплоёмкость может зависеть от температуры, поэтому более корректной является следующая формула с малыми (формально бесконечно малыми) :

Удельная теплоемкость — это количество теплоты, необходимое для нагревания 1 кг вещества на 1 К:   Молярная теплоемкость — количество теплоты, необходимое для нагревания 1 моль вещества на 1 К: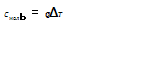   Удельная и молярная теплоемкости связаны соотношением: , где М — молярная масса (масса одного моля вещества).

Удельная и молярная теплоемкости газа при постоянном объеме, постоянном давлении. При постоянном объеме работа газа равна нулю (А=0) и все полученное тепло идет на увеличение внутренней энергии газа ( ). Молярная теплоемкость газа при постоянном объеме: При постоянном давлении тепло Q, полученное газом, идет на увеличение внутренней энергии газа   и совершение работы A над внешними телами:  . Молярная теплоемкость газа при постоянном давлении:  . Таким образом, теплоемкость газа при постоянном давлении связана с теплоемкостью газа при постоянном объеме соотношениями: .

МАЙЕРА УРАВНЕНИЕ - ур-ние, устанавливающее связь между теплоёмкостями при пост, давлении  Cp и пост. объёме С_V 1 кмоля  идеального газа: ,  где R -газовая постоянная .Впервые было получено Ю. P. Майером в 1842 и ещё до работ Дж. П. Джоуля использовано им для количеств, определения механического эквивалента теплоты. Для произвольной массы т (кг) вещества в состоянии идеального газа M. у. записывается в виде:   , где  - молекулярная масса газа. M. у. можно получить из общего соотношения ,если учесть, что для идеального газа справедливо Клапейрона уравнение.

24.Тепловые машины. Тепловые двигатели. КПД тепловых двигателей. Второй закон термодинамики. Обратимые и необратимые процессы. Энтропия системы и закон возрастания энтропии. Цикл Карно. КПД цикла. Карно.

Теплово́й дви́гатель — устройство, совершающее работу за счет использования внутренней энергии топлива, тепловая машина, превращающая тепло в механическую энергию, использует зависимость теплового расширения вещества от температуры. (Возможно использование изменения не только объёма, но и формы рабочего тела, как это делается в твёрдотельных двигателях, где в качестве рабочего тела используется вещество в твёрдой фазе.) Действие теплового двигателя подчиняется законам термодинамики. Для работы необходимо создать разность давлений по обе стороны поршня двигателя или лопастей турбины. Для работы двигателя обязательно наличие топлива. Это возможно при нагревании рабочего тела (газа), который совершает работу за счёт изменения своей внутренней энергии. Повышение и понижение температуры осуществляется, соответственно, нагревателем и охладителем.

КПД теплово́го дви́гателя — отношение совершённой полезной работы двигателя, к энергии, полученной от нагревателя. КПД теплового двигателя может быть вычислен по следующей формуле где  — количество теплоты, полученное от нагревателя,  —  — количество теплоты, отданное холодильнику. Наибольшим КПД среди циклических машин, оперирующих при заданных температурах горячего источника T₁ и холодного T₂, обладают тепловые двигатели, работающие по циклу Карно; этот предельный КПД равен Второй закон термодинамики. Второй закон связан с понятием энтропии, являющейся мерой хаоса (или мерой порядка). Второй закон термодинамики гласит, что для вселенной в целом энтропия возрастает. Существует два классических определения второго закона термодинамики :

Кельвина и Планка Не существует циклического процесса, который извлекает количество теплоты из резервуара при определенной температуре и полностью превращает эту теплоту в работу. (Невозможно построить периодически действующую машину, которая не производит ничего другого, кроме поднятия груза и охлаждения резервуара теплоты)

Клаузиуса Не существует процесса, единственным результатом которого является передача количества теплоты от менее нагретого тела к более нагретому. (Невозможен круговой процесс, единственным результатом которого было бы производство работы за счет охлаждения теплового резервуара) Оба определения второго закона термодинамики опираются на первый закон термодинамики, утверждающий, что энергия убывает.Второй закон связан с понятием энтропии (S). Энтропия системы есть функция ее состояния, определенная с точностью до произвольной постоянной. Разность энтропий в двух равновесных состояниях 2 и 1, по определению, равна приведенному количеству теплоты, которое надо сообщить системе, чтобы перевести ее из состояния 1 в состояние 2 по любому квазистатическому пути. Энтропия порождается всеми процессами, она связана с потерей системы способности совершать работу. Рост энтропии - стихийный процесс. Если объем и энергия системы постоянны, то любое измение в системе увеличивает энтропию. Если же объем или энергия системы меняются, энтропия системы уменьшается. Однако, энтропия вселенной при этом не уменьшается.

Для того, чтобы энергию можно было использовать, в системе должны быть области с высоким и низким уровнями энергии. Полезная работа производится в результате передачи энергии от области с высоким уровнем энергии к области с низким уровнем энергии. -100% энергии не может быть преобразовано в работу - Энтропия может вырабатываться, но не может быть уничтожена. Закон возрастания энтропии. «В изолированной системе энтропия не уменьшается».Если в некоторый момент времени замкнутая система находится в неравновесном макроскопическом состоянии, то в последующие моменты времени наиболее вероятным следствием будет монотонное возрастание ее энтропии. Закон неубывания энтропии или так называемый физический смысл второго закона термодинамики был открыт Клаузиусом (1865), а его теоретическое обоснование было даноБольцманом (1870-е годы).

Если в некоторый момент времени энтропия замкнутой системы отлична от максимальной, то в последующие моменты энтропия не убывает — увеличивается или в предельном случае остается постоянной.

Обратимые и необратимые процессы, пути изменения состояния термодинамической системы. Процесс называют обратимым, если он допускает возвращение рассматриваемой системы из конечного состояния в исходное через ту же последовательность промежуточных состояний, что и в прямом процессе, но проходимую в обратном порядке. Обратимый процесс возможен, если и в системе, и в окружающей среде он протекает равновесно. При этом предполагается, что равновесие существует между отдельными частями рассматриваемой системы и на границе с окружающей средой. Обратимый процесс - идеализированный случай, достижимый лишь при бесконечно медленном изменении термодинамических параметров. Скорость установления равновесия должна быть больше, чем скорость рассматриваемого процесса. Если невозможно найти способ вернуть и систему, и тела в окружающей среде в исходное состояние, процесс изменения состояния системы называют необратимым. Необратимые процессы могут протекать самопроизвольно только в одном направлении; таковы диффузия,теплопроводность, вязкое течение и другое. Для химической реакции применяют понятия термодинамической и кинетической обратимости, которые совпадают только в непосредственной близости к состоянию равновесия. Р-ция А + В  С + D наз. кинетически обратимой или двусторонней, если в данных условиях продукты С и D могут реагировать друг с другом с образованием исходных веществ А и В. При этом скорости прямой и обратной реакций, соотв.  и  , где  и  -константы скорости, [А], [В], [С], [D]- текущие концентрации (активности), с течением времени становятся равными и наступает химическое равновесие, в котором  -константа равновесия, зависящая от температуры. Кинетически необратимыми (односторонними) являются обычно такие реакции, в ходе которых хотя бы один из продуктов удаляется из зоны реакции (выпадает в осадок, улетучивается или выделяется в виде малодиссоциированного соединения), а также реакции, сопровождающиеся выделением большого кол-ва тепла. В термодинамике цикл Карно́ или процесс Карно — это обратимый круговой процесс, состоящий из двух адиабатических и двухизотермических процессов. В процессе Карно термодинамическая система выполняет механическую работу и обменивается теплотой с двумя тепловым и резервуарами, имеющими постоянные, но различающиеся температуры. Резервуар с более высокой температурой называется нагревателем, а с более низкой температурой — холодильником.

Цикл Карно назван в честь французского учёного и инженера Сади Карно, который впервые его описал в своём сочинении «О движущей силе огня и о машинах, способных развивать эту силу» в 1824 году.

Поскольку обратимые процессы могут осуществляться лишь с бесконечно малой скоростью, мощность тепловой машины в цикле Карно равна нулю. Мощность реальных тепловых машин не может быть равна нулю, поэтому реальные процессы могут приближаться к идеальному обратимому процессу Карно только с большей или меньшей степенью точности. В цикле Карно тепловая машина преобразует теплоту в работу с максимально возможным коэффициентом полезного действия из всех тепловых машин, у которых максимальная и минимальная температуры в рабочем цикле совпадают соответственно с температурами нагревателя и холодильника в цикле Карно^. КПД тепловой машины Карно: Количество теплоты, полученное рабочим телом от нагревателя при изотермическом расширении, равно Аналогично, при изотермическом сжатии рабочее тело отдаёт холодильнику Отсюда коэффициент полезного действия тепловой машины Карно равен . «В изолированной системе энтропия не уменьшается».

Если в некоторый момент времени замкнутая система находится в неравновесном макроскопическом состоянии, то в последующие моменты времени наиболее вероятным следствием будет монотонное возрастание ее энтропии.

Закон неубывания энтропии или так называемый физический смысл второго закона термодинамики был открыт Клаузиусом (1865), а его теоретическое обоснование было даноБольцманом (1870-е годы). Если в некоторый момент времени энтропия замкнутой системы отлична от максимальной, то в последующие моменты энтропия не убывает — увеличивается или в предельном случае остается постоянной.

25. Явления переноса. Явления переноса. Равновесные и неравновесные процессы. Экспериментальные законы диффузии, теплопроводности и внутреннего трения. Молекулярно-кинетическая теория явлений переноса.

Явления переноса: В термодинамически неравновесных системах возникают особые необратимые процес­сы, называемые явлениями переноса, в результате которых происходит пространственный перенос энергии, массы, импульса. К явлениям переноса относятся теплопроводность (обусловлена переносом энергии),диффузия (обусловлена переносом массы) и внутреннее трение (обусловлено переносом импульса). Для простоты ограничимся одномерными явлениями переноса. Систему отсчета выберем так, чтобы ось х была ориентирована в направлении переноса. 1. Теплопроводность. Если в одной области газа средняя кинетическая энергия молекул больше, чем в другой, то с течением времени вследствие постоянных сто­лкновений молекул происходит процесс выравнивания средних кинетических энергий молекул, т. е., иными словами, выравнивание температур. Перенос энергии в форме теплоты подчиняется закону Фурье: где j_E  — плотность теплового потока — величина, определяемая энергией, переносимой в форме теплоты в единицу времени через единичную площадку,перпендикулярную оси х, l — теплопроводность,    — градиент температуры, равный скорости изменения температуры на единицу длины х в направлении нормали к этой площадке. Знак минус показывает, что при теплопроводности энергия переносится в направлении убывания температуры (поэтому знаки j_E  и  – противоположны). Теплопроводность l численно равна плотности теплового потока при градиенте температуры, равном единице.

2. Диффузия. Явление диффузии заключается в том, что происходит самопроиз­вольное проникновение и перемешивание частиц двух соприкасающихся газов, жидкостей и даже твердых тел; диффузия сводится к обмену масс частиц этих тел, возникает и продолжается, пока существует градиент плотности. Во время становления молекулярно-кинетической теории по вопросу диффузии возникли противоречия. Так как молекулы движутся с огромными скоростями, диффузия должна происходить очень быстро. Если же открыть в комнате сосуд с пахучим веществом, то запах распространяется довольно медленно. Однако противоречия здесь нет. Молекулы при атмосферном давлении обладают малой длиной свободного пробега и, сталкиваясь с другими молекулами, в основном «стоят» на месте. Явление диффузии для химически однородного газа подчиняется закону Фука: где j_m — плотность потока массы — величина, определяемая массой вещества, диффундирующего в единицу времени через единичную площадку,перпендикулярную оси х, D — диффузия (коэффициент диффузии), dr/dx — градиент плотности, равный скорости изменения плотности на единицу длины хв направлении нормали к этой площадке. Знак минус показывает, что перенос массы происходит в направлении убывания плотности (поэтому знаки j_m и dr/dxпротивоположны). Диффузия D численно равна плотности потока массы при градиенте плотности, равном единице.  3. Внутреннее трение (вязкость).

Механизм возникновения внутреннего трения меж­ду параллельными слоями газа (жидкости), движущимися с различными скоростями, заключается в том, что из-за хаотического теплового движения происходит обмен молекулами между слоями, в результате чего импульс слоя, движущегося быстрее, уменьшается, движущегося медленнее — увеличивается, что приводит к торможению слоя, движущегося быстрее, и ускорению слоя, движущегося медленнее. сила внутреннего трения между двумя слоями газа (жидкости) подчиняется закону Ньютона: , где h — динамическая вязкость (вязкость), dv/dx — градиент скорости, показывающий быстроту изменения скорости в направлении х, перпендикулярном направлению дви­жения слоев, S — площадь, на которую действует сила F.

Неравновесные процессы Вследствие необратимости термодинамических процессов все процессы в изолированной системе протекают лишь в одном направлении — в направлении приближения системы к состоянию теплового равновесия. Будучи выведена из состояния равновесия, система переходит в новое состояние равновесия спустя некоторое время — время релаксации. Оно зависит от температуры, давления, плотности системы, а также от характера взаимодействия между частицами. Переход системы к равновесному состоянию представляет собой необратимый процесс, поскольку вероятность самопроизвольного перехода равновесной системы в неравновесное состояние ничтожно мала.

Равнове́сный процесс — тепловой процесс, в котором система проходит непрерывный ряд бесконечно близких равновесных термодинамических состояний.Равновесный тепловой процесс называется обратимым, если его можно провести обратно и в телах, окружающих систему, не останется никаких изменений.Реальные процессы изменения состояния системы всегда происходят с конечной скоростью, поэтому не могут быть равновесными. Реальный процесс изменения состояния системы будет тем ближе к равновесному, чем медленнее он совершается, поэтому равновесные процессы называют квазистатическими. Молекулярно-кинетическая теория явлений переноса. законы Фурье, Фика и Ньютона не вскрывают молекулярно-кинетической сути коэффициентов λ, D и η. Выражения для коэффициентов переноса получаются из кинетической теории. Они записаны без вывода, поскольку строгое и формальное рассмотрение явлений переноса довольно громоздко, а качественное — не имеет смысла. Формулы дают связь коэффициентов переноса и характеристики теплового движения молекул. Из этих формул следуют простые зависимости между λ, D и η:  и   

26. Уравнение Ван-дер-Ваальса. Реальные газы. Силы и потенциальная энергия межмолекулярного взаимодействия. Уравнение Ван-дер-Ваальса. Критическое состояние газа и его параметры. Реальный газ — газ, который не описывается уравнением состояния идеального газа Клапейрона — Менделеева.

Зависимости между его параметрами показывают, что молекулы в реальном газе взаимодействуют между собой и занимают определенный объём. Состояние реального газа часто на практике описывается обобщённым уравнением Менделеева — Клапейрона: где p — давление; V — объем; T — температура; Z_r = Z_r (p,T)  — коэффициент сжимаемости газа; m — масса; М — молярная масса; R — газовая постоянная.

Силы и потенциальная энергия межмолекулярного взаимодействия. При рассмотрении реальных газов — газов, свойства которых зависят от взаимо­действия молекул, надо учитывать силы межмолекулярного взаимодействия. Они прояв­ляются на расстояниях £ 10^–9 м и быстро убывают при увеличении расстояния между молекулами. Такие силы называются короткодействующими. По мере развития представлений о строении атома и квантовой механики, было выяснено, что между молекулами вещества одновременно действуют силы притяжения и силы отталкивания. На рис. А  приведена качественная зависимость сил межмолекулярного взаимодействия от расстояния r между молекулами, где F_о и F_п — соответственно силы отталкивания и притяжения, a F — их результирующая. Силы отталкивания считаются положительными, а силы взаимного притяжения — отрицательными.

На расстоянии r=r₀ результирующая сила F = 0, т.е. силы притяжения и оттал­кивания уравновешивают друг друга. Таким образом, расстояние r₀ соответствует равновесному расстоянию между молекулами, на котором бы они находились в отсут­ствие теплового движения. При r < r₀ преобладают силы отталкивания (F>0), при r > r₀ — силы притяжения (F<0). На расстояниях r > 10^–9 м межмолекулярные силы взаимодействия практически отсутствуют (F®0).

Элементарная работа dA силы F при увеличении расстояния между молекулами на dr совершается за счет уменьшения взаимной потенциальной энергии молекул, т. е. Из анализа качественной зависимости потенциальной энергии взаимодействия молекул от расстояния между ними (рис. б) следует, что если молекулы находятся друг от друга на расстоянии, на котором межмолекулярные силы взаимодействия не действу­ют (r®¥), то П=0. При постепенном сближении молекул между, ними появляются силы притяжения (F<0), которые совершают положительную работу (dA=Fdr > 0). Тогда, согласно (60.1), потенциальная энергия взаимодействия уменьшается, достигая минимума при r= r₀. При r < r₀ с уменьшением r силы отталкивания (F>0) резко возрастают и совершаемая против них работа отрицательна (dA=Fdr<0). Потенци­альная энергия начинает тоже резко возрастать и становится положительной. Из данной потенциальной кривой следует, что система из двух взаимодействующих молекул в состоянии устойчивого равновесия (r = r₀) обладает минимальной потенци­альной энергией.Критерием различных агрегатных состояний вещества является соотношение меж­ду величинами П_min и kT. П_min — наименьшая потенциальная энергия взаимодействия молекул — определяет работу, которую нужно совершить против сил притяжения для того, чтобы разъединить молекулы, находящиеся в равновесии (r= r₀); kT определяет удвоенную среднюю энергию, приходящуюся на одну степень свободы хаотического (теплового) движения молекул.

Если П_min<<kT, то вещество находится в газообразном состоянии, так как интенсивное тепловое движение молекул препятствует соединению молекул, сблизившихся до расстояния r₀, т. е. вероятность образования агрегатов из молекул достаточно мала. Если П_min>>kT, то вещество находится в твердом состоянии, так как молекулы, 27/притягиваясь друг к другу, не могут удалиться на значительные расстояния и колеблются около положений равновесия, определяемого расстоянием r₀. Если П_min»kT, то вещество находится в жидком состоянии, так как в результате теплового движения молекулы перемещаются в пространстве, обмениваясь местами, но не расходясь на расстояние, превышающее r₀. Таким образом, любое вещество в зависимости от температуры может находиться в газообразном, жидком или твердом агрегатном состоянии, причем температура перехода из одного агрегатного состояния в другое зависит от значения П_min, для данного вещества. Например, у инертных газов П_min мало, а у металлов велико, поэтому при обычных (комнатных) температурах они находятся соответственно в газо­образном и твердом состояниях. Уравнение состояния газа Ван-дер-Ваальса — уравнение, связывающее основные термодинамические величины в модели газа Ван-дер-Ваальса. Термическим уравнением состояния (или, часто, просто уравнением состояния) называется связь между давлением, объёмом и температурой. Для одного моля газа Ван-дер-Ваальса оно имеет вид: где

p — давление,  — молярный объём,T — абсолютная температура,R — универсальная газовая постоянная. Видно, что это уравнение фактически является уравнением состояния идеального газа с двумя поправками. Поправка a  учитывает силы притяжения между молекулами (давление на стенку уменьшается, так как есть силы, втягивающие молекулы приграничного слоя внутрь), поправка b — объем молекул газа. Для v  молей газа Ван-дер-Ваальса уравнение состояния выглядит так: где V  — объём, Критическое состояние - состояние двухфазной системы, в котором сосуществующие в равновесии фазы становятся тождественными по всем своим свойствам. Параметры критического состояния системы (давление р_к, т-ра Т_к, объем V_к, состав x_к и др.) наз. критич. параметрами. За пределами критическое состояние сосуществование рассматриваемых фаз в равновесии невозможно, система превращ. в однофазную (гомогенную). В этом смысле критическое состояние является предельным случаем двухфазного равновесия. В критическом состояния поверхностное (межфазное) натяжение на границе раздела сосуществующих фаз равно нулю, поэтому вблизи критическое состояние легко образуются системы, состоящие из мн. капель или пузырьков (эмульсии, аэрозоли, пены). Вблизи критического состояния резко возрастает величина флуктуации плотности (в случае чистых веществ) и концентраций компонентов (в многокомпонентных системах), что приводит к значит. изменению ряда физ. свойств вещества. Критические параметры газа называются значения его макропараметров (давления, объёма и температуры) в критической точке, т.е. в таком состоянии, когда жидкая и газообразная фазы вещества неразличимы. Найдем эти параметры для газа Ван-дер-Ваальса, для чего преобразуем уравнение состояния:

Мы получили уравнение третьей степени относительно V.

В критической точке все три корня уравнения сливаются в один, поэтому предыдущее уравнение эквивалентно следующему:

Приравняв коэффициенты при соответствующих степенях V, получим равенства:

Из них вычислим значения критических параметров... .и критического коэффициента:

27. Фазовые переходы первого и второго рода. Сравнение изотерм Ван-дер-Ваальса с экспериментальными изотермами. Фазы и условия равновесия фаз. Уравнение Клайперона-Клаузиуса. Фазовые диаграммы. Фазовые переходы первого и второго рода.  Сравнение изотерм Ван-дер-Ваальса с экспериментальными изотемами. Физическая сущность уравнения Ван-дер-Ваальса выясняется при рассмотрении экспериментальных изотерм, полученных в 1868 г. Т. Эндрюсом при исследовании углекислоты (рис.).

 

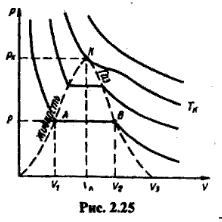
Как показывают экспериментальные изотермы, при переход вещества из одной фазы в другую совершается при постоянном давлении р (прямая АВ на рис. ). Если из исследуемой жидкости предварительно удалить воздух и различные примеси, то экспериментально можно обнаружить участок изотермы АВ (см. рис). Участок изотермы АВ описывает перегретую жидкость, т. е. такую жидкость, которая при температуре кипения некоторое время не переходит в пар, расширяясь по кривой АВ. По мере повышения температуры горизонтальные участки изотерм (линия конденсации АВ) (рис. ) становятся все более короткими, при некоторой температуре  линия конденсации исчезает, т. е. начиная с температуры  состояние вещества становится однофазным; температуру Г„ называют критической. Это наибольшая температура, при которой газ может быть еще превращен в жидкость. На изотерме, соответствующей критической температуре, точки А и В сливаются в одну точку К, характеризующуюся такими координатами: VK — критический объем, рк — критическое давление. В критической точке все три корня уравнения должны совпадать. Из этого условия получают значения критических параметров: Если на различных изотермах соединить все точки, при которых начинается процесс кипения, пунктирной линией (рис. ), то эта линия разделит диаграмму р, V на три области. Справа и слева от этой линии вещество находится в однофазном состоянии, справа и выше изотермы Тк — газообразное, слева — жидкое, внутри очерченной области — двухфазовое состояние жидкость — пар. ФАЗА в термодинамике, термодинамически равновесное состояние в-ва, отличающееся по физ. св-вам от др. возможных равновесных состояний (др. фаз) того же в-ва (см. Равновесие термодинамическое). Иногда неравновесное метастабильное состояние в-ва также наз. фазой (метастабильной). Переход в-ва из одной Ф. в другую — фазовый переход — связан с качеств. изменениями св-в в-ва. Напр., газовое, жидкое и крист. состояния (Ф.) в-ва различаются хар-ром движения структурных ч-ц (атомов, молекул) и наличием или отсутствием упорядоченной структуры (см. Агрегатные состояния). Различные крист. Ф. могут отличаться друг от друга типом крист. структуры, электропроводностью, электрич. и магн. св-вами, наличием или отсутствием сверхпроводимости и т. д. Жидкие Ф. отличаются друг от друга концентрацией компонентов, наличием или отсутствием сверхтекучести, анизотропией упругих и электрич. св-в (у жидких кристаллов) и т. д. В тв. сплавах Ф. крист. структуры могут отличаться плотностью, модулями упругости, темп-рой плавления и др. свойствами.Равнове́сие фаз в термодинамике — состояние, при котором фазы в термодинамической системе находятся в состоянии теплового, механическогои химического равновесия.Типы фазовых равновесий: Тепловое равновесие означает, что все фазы вещества в системе имеют одинаковую температуру. Механическое равновесие означает равенство давлений по разные стороны границы раздела соприкасающихся фаз. Строго говоря, в реальных системах эти давления равны лишь приближенно, разность давлений создается поверхностным натяжением. Химическое равновесие выражается в равенстве химических потенциалов всех фаз вещества. Условие равновесия фаз Рассмотрим химически однородную систему (состоящую из частиц одного типа). Пусть в этой системе имеется граница раздела между фазами 1 и 2. Как было указано выше, для равновесия фаз требуется равенство температур и давлений на границе раздела фаз. Известно (см. статьюТермодинамические потенциалы), что состояние термодинамического равновесия в системе с постоянными температурой и давлением соответствует точке минимума потенциала Гиббса.

Потенциал Гиббса такой системы будет равен где   и   — химические потенциалы, а  N1 и N2 — числа частиц в первой и второй фазах соответственно. При этом сумма   (полное число частиц в системе) меняться не может, поэтому можно записать . Предположим, что  , для определенности,  . Тогда, очевидно, минимум потенциала Гиббса достигается при N1=N (все вещество перешло в первую фазу). Таким образом, равновесие фаз возможно только в том случае, когда химические потенциалы этих фаз по разные стороны границы раздела равны: .

Уравнение Клапейрона — Клаузиуса — термодинамическое уравнение, относящееся к квазистатическим (равновесным) процессам перехода вещества из одной фазы в другую (испарение, плавление, сублимация, полиморфное превращение и др.). Согласно уравнению, теплота фазового перехода (например, теплота испарения, теплота плавления) при квазистатическом процессе определяется выражением где L — удельная теплота фазового перехода,   — изменение удельного объёма тела при фазовом переходе. Уравнение названо в честь его авторов, Рудольфа Клаузиуса и Бенуа Клапейрона. фазовая диаграмма иначе диаграмма состояния —графическое изображение состояний термодинамической системы в пространстве основных параметров состояния — температуры T, давления p и состава x. Фазовые диаграммы позволяют узнать, какие фазы (т. е. однородные подсистемы, отличающиеся строением и/или свойствами от других) могут присутствовать в данной системе при данных условиях и составе. Для сложных систем, состоящих из многих фаз и компонентов, построение диаграмм состояния по экспериментальным данным и данным термодинамического моделирования является важнейшим способом предсказания поведения в ходе различных процессов. Анализ относительного расположения полей, разделяющих их поверхностей и линий, а также точек сочленения последних позволяет однозначно и наглядно определять условия фазовых равновесий, появления в системе новых фаз и химических соединений, образования и распада жидких и твердых растворов и т. п. Фазовые переходы первого и второго рода. Переход вещества от одной фазы в другую – фазовый переход – всегда связан с качественными изменениями свойств вещества. Примером фазового перехода могут служить изменения агрегатного состояния вещества или переходы, связанные с изменениями в составе, строении и свойствах вещества (например, переход кристаллического вещества из одной модификации в другую). Различают фазовые переходы двух родов. Фазовый переход первого рода (например, плавление, кристаллизация и т.д.) сопровождается поглощением или выделением вполне определённого количества теплоты, называемой теплотой фазового перехода.  Фазовые переходы первого рода характеризуются постоянством температуры, изменениями энтропии и объёма. Объяснение этому можно дать следующим образом. Например, при плавлении телу нужно сообщить некоторое количество теплоты, чтобы вызвать разрушение кристаллической решётки. Подводимая при плавлении теплота идёт не на нагрев тела, а на разрыв межатомных связей, поэтому плавление протекает при постоянной температуре. При подобных переходах – из более упорядоченного кристаллического состояния в менее упорядоченное жидкое состояние – степень беспорядка увеличивается и, с точки зрения второго начала термодинамики, этот процесс связан с возрастанием энтропии системы. Если переход происходит в обратном направлении (кристаллизация), то система теплоту выделяет.

Верхняя ветвь отвечает кристаллическому состоянию, а нижняя ветвь представляет свободную энергию парообразной фазы. При низких температурах свободная энергия кристалла меньше, чем пара, и, следовательно, кристаллическое состояние выгоднее. При высоких температурах, наоборот, выгоднее существование парообразного состояния.

При теоретическом описании фазовых переходов первого рода каждую из фаз обычно описывают отдельно. Так, кристаллическую ветвь рассматривают, пользуясь моделью идеального кристалла, т. е. предполагая регулярное расположение всех атомов. Парообразную же ветвь получают, используя модель идеального газа, предполагающую полный беспорядок в системе. Зависимости, полученные для различных моделей, накладывают друг на друга и исследуют, какая из возможностей реализуется в данных условиях. Получить описание фазового перехода первого рода, одновременно учитывая все состояния системы, до настоящего времени не удается из-за огромных математических трудностей.  Фазовые переходы, не связанные с поглощением или выделением теплоты и изменением объёма, называются фазовыми переходами второго рода. Эти переходы характеризуются постоянством объёма и энтропии, но скачкообразным изменением теплоёмкости. Общая трактовка фазовых переходов второго рода предложена советским учёным Л.Д.Ландау (1908-1968). Согласно этой трактовке, фазовые переходы второго рода связаны с изменением симметрии: выше точки перехода система, как правило, обладает более высокой симметрией, чем ниже точки перехода. Примерами фазовых переходов второго рода являются: переход ферромагнитных веществ (железа, никеля) при определённых давлении и температуре в парамагнитное состояние; переход металлов и некоторых сплавов при температуре, близкой к 0К, в сверхпроводящее состояние, характеризуемое скачкообразным уменьшением электрического сопротивления до нуля; превращение обыкновенного жидкого гелия при Т=2,9К в другую жидкую модификацию, обладающую свойствами сверхтекучести.