
- •1.Кинематика прямолинейного движения материальной точки. Материальная точка. Система отсчета. Скорость и ускорение. Траектория, путь, перемещение.
- •Сложение сил.
- •Уравнения движения в неинерциальных системах отсчета.
- •Работа внешних сил при вращении твердого тела
- •Период, декремент затухания, добротность колебания. Период затухающих колебаний
- •Следствия из преобразований Лоренца: изменение длин промежутков времени, закон сложения скоростей.
- •21. Первый закон термодинамики. Закон распределения кинетической энергии молекул по степеням свободы. Внутренняя энергия идеального газа. Работа расширения газа. Первый закон термодинамики.
Период, декремент затухания, добротность колебания. Период затухающих колебаний
.Логарифмический
декремент затухания ![]() ,
подставим A(t)
= A0-βt.
,
подставим A(t)
= A0-βt.
![]() =
=![]()
![]() Добро́тность —
свойство колебательной
системы,
определяющее полосу резонанса и
показывающее, во сколько раз запасы
энергии в системе больше, чем потери
энергии за один период колебаний.
Добро́тность —
свойство колебательной
системы,
определяющее полосу резонанса и
показывающее, во сколько раз запасы
энергии в системе больше, чем потери
энергии за один период колебаний.
Добротность обратно пропорциональна скорости затухания собственных колебаний в системе. То есть, чем выше добротность колебательной системы, тем меньше потери энергии за каждый период и тем медленнее затухают колебания.
Общая
формула для добротности любой колебательной
системы: ![]() где:
где: ![]() —
резонансная частота колебаний W —
энергия, запасённая в колебательной
системе
—
резонансная частота колебаний W —
энергия, запасённая в колебательной
системе ![]() —
рассеиваемая мощность.
—
рассеиваемая мощность.
15. Вынужденные колебания. Вынужденные колебания. Дифференциальное уравнение вынужденных колебаний и его решение. Амплитуда и фаза вынужденных колебаний. Явление резонанса. Резонансные кривые. Вынужденные колебания Колебания, совершающиеся под воздействием внешней периодической силы, называются вынужденными.В этом случае внешняя сила совершает положительную работу и обеспечивает приток энергии к колебательной системе. Она не дает колебаниям затухать, несмотря на действие сил трения.Периодическая внешняя сила может изменяться во времени по различным законам. Особый интерес представляет случай, когда внешняя сила, изменяющаяся по гармоническому закону с частотой ω, воздействует на колебательную систему, способную совершать собственные колебания на некоторой частоте ω0.Если свободные колебания происходят на частоте ω0, которая определяется параметрами системы, то установившиеся вынужденные колебания всегда происходят начастоте ω внешней силы. Дифференциальное уравнение вынужденных колебаний и его решение Колебания возникающие под действием внешней периодически изменяющейся силы называются вынужденными колебаниями. Механическoе: Обознач м:b=h/2m-коэффициент затухания ; w02=k/m-собственная частота свободных колебаний.f0=F0/m x¢¢+2bх¢+w02х=f0coswt-неоднородное линейное уравнение 2-го порядка
Решение:
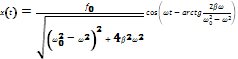 В случае вынужденных колебаний кроме
двух названных сил — упругой и силы
сопротивления, на систему действует
ещё одна сила: F = F0Coswt.
В случае вынужденных колебаний кроме
двух названных сил — упругой и силы
сопротивления, на систему действует
ещё одна сила: F = F0Coswt.![]() —
дифференциальное уравнение вынужденных
колебаний пружинного маятника. Это
уравнение движения принято записывать
так:Амплитуда
и фаза вынужденных колебаний. Явление
резонанса. Резонансные кривые
Амплитуда вынужденных колебаний прямо
пропорциональна амплитуде возмущающего
усилия F0.
—
дифференциальное уравнение вынужденных
колебаний пружинного маятника. Это
уравнение движения принято записывать
так:Амплитуда
и фаза вынужденных колебаний. Явление
резонанса. Резонансные кривые
Амплитуда вынужденных колебаний прямо
пропорциональна амплитуде возмущающего
усилия F0.
Резона́нс — явление резкого возрастания амплитуды вынужденных колебаний, которое наступает при приближении частоты внешнего воздействия к некоторым значениям (резонансным частотам), определяемым свойствами системы. Увеличение амплитуды — это лишь следствие резонанса, а причина — совпадение внешней (возбуждающей) частоты с внутренней (собственной) частотой колебательной системы. При помощи явления резонанса можно выделить и/или усилить даже весьма слабые периодические колебания. Резонанс — явление, заключающееся в том, что при некоторой частоте вынуждающей силы колебательная система оказывается особенно отзывчивой на действие этой силы. Степень отзывчивости в теории колебаний описывается величиной, называемой добротность. Явление резонанса впервые было описано Галилео Галилеем в 1602 г в работах, посвященных исследованию маятников и музыкальных струн.
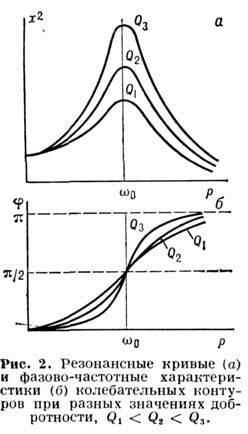
Зависимость амплитуды х стационарных вынужденных колебаний от частоты pвынуждающей силы при постоянной её амплитуде наз. резонансной кривой (рис. 2). В линейном колебат. контуре резонансные кривые, соответствующие различным F, подобны, а фазово-частотная характеристика f(p) не зависит от амплитуды силы
16.
Сложение гармонических колебаний.
Сложение
гармонических колебаний одного
направления и одинаковой частоты.
Сложение колебаний одного направления
с разными частотами, биение. Сложение
взаимно перпендикулярных колебаний.
Фигуры Лиссажу. Сложение
гармонических колебаний одного
направления и одинаковой частоты
При наложении двух гармонических
колебаний, происходящих в одном
направлении с одинаковой частотой,
возникает гармоническое колебание с
той же частотой, а его амплитуда зависит
от амплитуд и начальных фаз отдельных
колебаний. Результирующее отклонение
в каждый момент времени равно алгебраической
сумме составляющих отклонений.
Колеблющееся тело может принимать
участие в нескольких колебательных
процессах, тогда следует найти
результирующее колебание, другими
словами, колебания необходимо сложить.
В данном разделе будем складывать
гармонические колебания одного
направления и одинаковой частоты
![]() применяя метод вращающегося вектора
амплитуды, построим графически векторные
диаграммы этих колебаний (рис. 1). Tax как
векторы A1 и A2 вращаются
с одинаковой угловой скоростью ω0,
то разность фаз (φ2 -
φ1)
между ними будет оставаться постоянной.
Значит, уравнение результирующего
колебания будет
применяя метод вращающегося вектора
амплитуды, построим графически векторные
диаграммы этих колебаний (рис. 1). Tax как
векторы A1 и A2 вращаются
с одинаковой угловой скоростью ω0,
то разность фаз (φ2 -
φ1)
между ними будет оставаться постоянной.
Значит, уравнение результирующего
колебания будет
![]() В формуле (1) амплитуда А и начальная
фаза φ соответственно определяются
выражениями
В формуле (1) амплитуда А и начальная
фаза φ соответственно определяются
выражениями
![]()
![]() Значит, тело, участвуя в двух гармонических
колебаниях одного направления и
одинаковой частоты, совершает при этом
также гармоническое колебание в том же
направлении и с той же частотой, что и
складываемые колебания. Амплитуда
результирующего колебания зависит от
разности фаз (φ2 -
φ1)
складываемых колебаний.
Значит, тело, участвуя в двух гармонических
колебаниях одного направления и
одинаковой частоты, совершает при этом
также гармоническое колебание в том же
направлении и с той же частотой, что и
складываемые колебания. Амплитуда
результирующего колебания зависит от
разности фаз (φ2 -
φ1)
складываемых колебаний.  Сложение колебаний одного направления
с разными частотами, биение. При сложении
двух гармонических колебаний разной
частоты, происходящих в одном направлении,
возникает негармоническое колебание
Результирующее отклонение в каждый
момент времени также равно алгебраической
сумме отклонений составляющих колебаний.
С другой стороны, любые негармонические
колебания можно рассматривать как
результирующее ряда гармонических
колебаний и разложить его на эти
составляющие. Соответствующий
математический прием носит название
анализа Фурье. При упрощающем предположении
Ym1 =
Ym2 и
φ01 =
φ02 в
результате сложения двух колебаний с
близкими частотами возникают биения.
Биение - явление, возникающее
при наложении двух
периодических колебаний,
например, гармонических,
близких по частоте, выражающееся в
периодическом уменьшении и
увеличении амплитуды суммарного
сигнала.Частота изменения
амплитуды суммарного сигнала равна
разности частот исходных сигналов.
Биения возникают от того, что один из
двух сигналов линейно во времени отстаёт
от другого по фазе,
и, в те моменты, когда колебания
происходят синфазно,
суммарный сигнал оказывается максимален,
а в те моменты, когда два сигнала
оказываются в противофазе, они взаимно
гасят друг друга. Эти моменты периодически
сменяют друг друга по мере того, как
нарастает отставание. Сложение
взаимно перпендикулярных колебаний.
Найдем результат сложения двух
гармонических колебаний одинаковой
частоты ω, которые происходят во взаимно
перпендикулярных направлениях вдоль
осей х и у. Начало отсчета для простоты
выберем так, чтобы начальная фаза первого
колебания была равна нулю, и запишем
это в виде
Сложение колебаний одного направления
с разными частотами, биение. При сложении
двух гармонических колебаний разной
частоты, происходящих в одном направлении,
возникает негармоническое колебание
Результирующее отклонение в каждый
момент времени также равно алгебраической
сумме отклонений составляющих колебаний.
С другой стороны, любые негармонические
колебания можно рассматривать как
результирующее ряда гармонических
колебаний и разложить его на эти
составляющие. Соответствующий
математический прием носит название
анализа Фурье. При упрощающем предположении
Ym1 =
Ym2 и
φ01 =
φ02 в
результате сложения двух колебаний с
близкими частотами возникают биения.
Биение - явление, возникающее
при наложении двух
периодических колебаний,
например, гармонических,
близких по частоте, выражающееся в
периодическом уменьшении и
увеличении амплитуды суммарного
сигнала.Частота изменения
амплитуды суммарного сигнала равна
разности частот исходных сигналов.
Биения возникают от того, что один из
двух сигналов линейно во времени отстаёт
от другого по фазе,
и, в те моменты, когда колебания
происходят синфазно,
суммарный сигнал оказывается максимален,
а в те моменты, когда два сигнала
оказываются в противофазе, они взаимно
гасят друг друга. Эти моменты периодически
сменяют друг друга по мере того, как
нарастает отставание. Сложение
взаимно перпендикулярных колебаний.
Найдем результат сложения двух
гармонических колебаний одинаковой
частоты ω, которые происходят во взаимно
перпендикулярных направлениях вдоль
осей х и у. Начало отсчета для простоты
выберем так, чтобы начальная фаза первого
колебания была равна нулю, и запишем
это в виде ![]() где α — разность фаз обоих колебаний,
А и В равны амплитудам складываемых
колебаний. Уравнение траектории
результирующего колебания определим
исключением из формул времени t. Записывая
складываемые колебания как
где α — разность фаз обоих колебаний,
А и В равны амплитудам складываемых
колебаний. Уравнение траектории
результирующего колебания определим
исключением из формул времени t. Записывая
складываемые колебания как
![]()
![]() и заменяя во втором/уравнении
и заменяя во втором/уравнении ![]() на
на ![]() и
и ![]() на
на ![]() ,
найдем после несложных преобразований
уравнение эллипса, у которого оси
ориентированы произвольно относительно
координатных/осей:
,
найдем после несложных преобразований
уравнение эллипса, у которого оси
ориентированы произвольно относительно
координатных/осей: ![]() Фигу́ры
Лиссажу́ — замкнутые
траектории,
прочерчиваемые точкой, совершающей
одновременно два гармонических
колебания в
в двух взаимно перпендикулярных
направлениях. Впервые изучены французским
учёным Жюлем
Антуаном Лиссажу.
Фигу́ры
Лиссажу́ — замкнутые
траектории,
прочерчиваемые точкой, совершающей
одновременно два гармонических
колебания в
в двух взаимно перпендикулярных
направлениях. Впервые изучены французским
учёным Жюлем
Антуаном Лиссажу.
17. Механика жидкости. Понятие потока, трубки тока, плоскости потока, стационарное течение идеальной жидкости. Уравнения неразрывности и Бернулли и Стокса. Уравнение Ньютона. Подъемная сила. Поток жидкости представляет собой совокупность элементарных струек жидкости. По этой причине основные кинематические характеристики потока во многом совпадают по своему смыслу с аналогичными характеристиками для элементарной струйки жидкости. Тем не менее, различия всё же имеются. Так в отличие от элементарной струйки, которая отделена от остальной жидкости поверхностью трубки тока, образованной линиями тока, поток жидкости имеет реальные границы в виде твёрдой среды, газообразной или жидкой сред.
![]() Поэтому живое
сечение потока
— криволинейная плоскость
(рис. линия I—I) В виду незначительного
расхождения векторов скорости в
гидродинамике за живое сечение принимается
плоскость, расположенная перпендикулярно
скорости движения жидкости в средней
точке потока. Стационарное
течение идеальной жидкости.
Поэтому живое
сечение потока
— криволинейная плоскость
(рис. линия I—I) В виду незначительного
расхождения векторов скорости в
гидродинамике за живое сечение принимается
плоскость, расположенная перпендикулярно
скорости движения жидкости в средней
точке потока. Стационарное
течение идеальной жидкости.
Течение жидкости представляет собой поле скоростей, изображенное с помощью линий тока. Если поле скоростей, то есть форма и расположение соответствующие ему линии тока не меняются с течением времени, то движение жидкости называется стационарным или установившимся.
Уравнение неразрывности потока отражает закон сохранения массы: количество втекающей жидкости равно количеству вытекающей. Например, на рис. 10 расходы во входном и выходном сечениях напорной трубы равны:
q1 = q2.
![]() С
учётом, что q = Vw,
получим уравнение неразрывности потока:
V1 w1
= V2 w2
. Если отсюда выразим скорость для
выходного сечения V2
= V1 w1 /w2
, то легко заметить, что она увеличивается
обратно пропорционально площади живого
сечения потока. Такая обратная зависимость
между скоростью и площадью является
важным следствием уравнения неразрывности
и применяется в технике, например, при
тушении пожара для получения сильной
и дальнобойной струи воды. Бернулли
уравнение, основное
уравнение гидродинамики,
связывающее (для установившегося
течения) скорость текущей жидкости v, давление
в ней р и
высоту h расположения
малого объёма жидкости над плоскостью
отсчёта. Б. у. было выведено Д. Бернулли
в 1738 для струйки идеальной несжимаемой
жидкости постоянной плотности r,
находящейся под действием только сил
тяжести. В этом случае Б. у. имеет вид:
v2/2
+ plr
+ gh =
const, где g
— ускорение
силы тяжести. Если это уравнение умножить
на r, то
1-й член будет представлять собой
кинетическую энергию единицы объёма
жидкости, а др. 2 члена — его потенциальную
энергию, часть которой обусловлена
силой тяжести (последний член уравнения),
а др. часть — давлением p. Б.
у. в такой форме выражает закон сохранения
энергии. Если вдоль струйки жидкости
энергия одного вида, например кинетическая,
увеличивается, то потенциальная энергия
на столько же уменьшается. Поэтому,
например, при сужении потока, текущего
по трубопроводу, когда скорость потока
увеличивается (т.к. через меньшее
сечение за то же время проходит такое
же количество жидкости, как и через
большее сечение), давление соответственно
в нём уменьшается (на этом основан
принцип работы расходомера Вентури).
Из Б. у. вытекает ряд важных следствий.
Например, при истечении жидкости из
открытого сосуда под действием силы
тяжести (рис.
1) из Б. у.
следует: v2/2g
= h или
С
учётом, что q = Vw,
получим уравнение неразрывности потока:
V1 w1
= V2 w2
. Если отсюда выразим скорость для
выходного сечения V2
= V1 w1 /w2
, то легко заметить, что она увеличивается
обратно пропорционально площади живого
сечения потока. Такая обратная зависимость
между скоростью и площадью является
важным следствием уравнения неразрывности
и применяется в технике, например, при
тушении пожара для получения сильной
и дальнобойной струи воды. Бернулли
уравнение, основное
уравнение гидродинамики,
связывающее (для установившегося
течения) скорость текущей жидкости v, давление
в ней р и
высоту h расположения
малого объёма жидкости над плоскостью
отсчёта. Б. у. было выведено Д. Бернулли
в 1738 для струйки идеальной несжимаемой
жидкости постоянной плотности r,
находящейся под действием только сил
тяжести. В этом случае Б. у. имеет вид:
v2/2
+ plr
+ gh =
const, где g
— ускорение
силы тяжести. Если это уравнение умножить
на r, то
1-й член будет представлять собой
кинетическую энергию единицы объёма
жидкости, а др. 2 члена — его потенциальную
энергию, часть которой обусловлена
силой тяжести (последний член уравнения),
а др. часть — давлением p. Б.
у. в такой форме выражает закон сохранения
энергии. Если вдоль струйки жидкости
энергия одного вида, например кинетическая,
увеличивается, то потенциальная энергия
на столько же уменьшается. Поэтому,
например, при сужении потока, текущего
по трубопроводу, когда скорость потока
увеличивается (т.к. через меньшее
сечение за то же время проходит такое
же количество жидкости, как и через
большее сечение), давление соответственно
в нём уменьшается (на этом основан
принцип работы расходомера Вентури).
Из Б. у. вытекает ряд важных следствий.
Например, при истечении жидкости из
открытого сосуда под действием силы
тяжести (рис.
1) из Б. у.
следует: v2/2g
= h или ![]() т. е. скорость жидкости в выходном
отверстии такова же, как при свободном
падении частиц жидкости с высоты h
Навье —
Стокса уравнения, дифференциальные
уравнения движения вязкой жидкости
(газа). Названы по имени Л. Навье и
Дж. Стокса.
Для несжимаемой (плотность r = const) и
ненагреваемой (температура Т =
const) жидкости Н. — С. у. в проекциях на
оси прямоугольной декартовой системы
координат (система трёх уравнений) имеют
вид
т. е. скорость жидкости в выходном
отверстии такова же, как при свободном
падении частиц жидкости с высоты h
Навье —
Стокса уравнения, дифференциальные
уравнения движения вязкой жидкости
(газа). Названы по имени Л. Навье и
Дж. Стокса.
Для несжимаемой (плотность r = const) и
ненагреваемой (температура Т =
const) жидкости Н. — С. у. в проекциях на
оси прямоугольной декартовой системы
координат (система трёх уравнений) имеют
вид
![]()
Здесь t —
время, x, у, z —
координаты жидкой частицы, vx, vy, vz —
проекции её скорости, X, Y, Z —
проекции объёмной силы, p —
давление, v =
m/r
— кинематический коэффициент вязкости
(m — динамический коэффициент вязкости),![]() Два других уравнения получаются
заменой x на у, у на z и z на x.
Н. — С. у. служат для определения vx, vy,vz, р как
функций x, у, z, t.
Чтобы замкнуть систему, к уравнениям
присоединяют уравнение неразрывности,
имеющее для несжимаемой жидкости вид:
Два других уравнения получаются
заменой x на у, у на z и z на x.
Н. — С. у. служат для определения vx, vy,vz, р как
функций x, у, z, t.
Чтобы замкнуть систему, к уравнениям
присоединяют уравнение неразрывности,
имеющее для несжимаемой жидкости вид:
![]() Для интегрирования уравнений требуется
задать начальные (если движение не
является стационарным) и граничные
условия, которыми для вязкой жидкости
являются условия прилипания к твёрдым
стендам. Нью́тоновская
жи́дкость (названная
так в честь Исаака
Ньютона) —
вязкая жидкость,
подчиняющаяся в своём течении закону
вязкого трения Ньютона,
то есть касательное
напряжение и градиент скорости
в такой жидкости линейно
зависимы.
Коэффициент пропорциональности между
этими величинами известен как вязкость.
Простое уравнение,
описывающее силы вязкости в
ньютоновской жидкости, во многом
определяющие ее поведение, основано
на сдвиговом
течении:
Для интегрирования уравнений требуется
задать начальные (если движение не
является стационарным) и граничные
условия, которыми для вязкой жидкости
являются условия прилипания к твёрдым
стендам. Нью́тоновская
жи́дкость (названная
так в честь Исаака
Ньютона) —
вязкая жидкость,
подчиняющаяся в своём течении закону
вязкого трения Ньютона,
то есть касательное
напряжение и градиент скорости
в такой жидкости линейно
зависимы.
Коэффициент пропорциональности между
этими величинами известен как вязкость.
Простое уравнение,
описывающее силы вязкости в
ньютоновской жидкости, во многом
определяющие ее поведение, основано
на сдвиговом
течении:
![]() где:
где: ![]() — касательное
напряжение,
вызываемое жидкостью, Па;
— касательное
напряжение,
вызываемое жидкостью, Па; ![]() —
динамический коэффициент вязкости —
коэффициент пропорциональности, Па·с;
—
динамический коэффициент вязкости —
коэффициент пропорциональности, Па·с;
![]() —
производная скорости в направлении,
перпендикулярном направлению сдвига,
с−1.
Это уравнение обычно используют при
течении жидкости в одном направлении,
когда вектор скорости течения можно
считать сонаправленным (параллельным)
во всех точках рассматриваемого объёма
жидкости.
Подъёмная
сила,
составляющая полной силы давления
жидкой или газообразной среды на
движущееся в ней тело, направленная
перпендикулярно к скорости тела (к
скорости центра тяжести тела, если оно
движется непоступательно). Возникает
П. с. вследствие несимметрии обтекания
тела средой. Например, при обтекании
крыла самолёта частицы среды, обтекающие
нижнюю поверхность, проходят за тот же
промежуток времени меньший путь, чем
частицы, обтекающие верхнюю, более
выпуклую поверхность и, следовательно,
имеют меньшую скорость. Но, согласно Бернулли
уравнению,
там, где скорость частиц меньше, давление
среды больше и наоборот. В результате
давление среды на нижнюю поверхность
крыла будет больше, чем на верхнюю, что
и приводит к появлению П. с.
—
производная скорости в направлении,
перпендикулярном направлению сдвига,
с−1.
Это уравнение обычно используют при
течении жидкости в одном направлении,
когда вектор скорости течения можно
считать сонаправленным (параллельным)
во всех точках рассматриваемого объёма
жидкости.
Подъёмная
сила,
составляющая полной силы давления
жидкой или газообразной среды на
движущееся в ней тело, направленная
перпендикулярно к скорости тела (к
скорости центра тяжести тела, если оно
движется непоступательно). Возникает
П. с. вследствие несимметрии обтекания
тела средой. Например, при обтекании
крыла самолёта частицы среды, обтекающие
нижнюю поверхность, проходят за тот же
промежуток времени меньший путь, чем
частицы, обтекающие верхнюю, более
выпуклую поверхность и, следовательно,
имеют меньшую скорость. Но, согласно Бернулли
уравнению,
там, где скорость частиц меньше, давление
среды больше и наоборот. В результате
давление среды на нижнюю поверхность
крыла будет больше, чем на верхнюю, что
и приводит к появлению П. с.
18. Элементы специальной теории относительности (СТО). Постулаты СТО, относительность понятия одновременности. Преобразования Лоренца. Следствия из преобразований Лоренца: изменение длин промежутков времени, закон сложения скоростей.
Постулаты СТО Постулат 1 (принцип относительности Эйнштейна). Любое физическое явление протекает одинаково во всех инерциальных системах отсчёта. Это означает, что форма зависимости физических законов от пространственно-временных координат должна быть одинаковой во всех ИСО, то есть законы инвариантны относительно переходов между ИСО. Принцип относительности устанавливает равноправие всех ИСО.Учитывая второй закон Ньютона (или уравнения Эйлера-Лагранжа в лагранжевой механике), можно утверждать, что если скорость некоторого тела в данной ИСО постоянна (ускорение равно нулю), то она должна быть постоянна и во всех остальных ИСО. Иногда это и принимают за определение ИСО.
Формально,
принцип относительности Эйнштейна
распространил классический принцип
относительности (Галилея) с механических
на все физические явления. Однако, если
учесть, что во времена Галилея физика
заключалась собственно в механике, то
и классический принцип тоже можно
считать распространяющимся на все
физические явления. В том числе он должен
распространяться и на электромагнитные
явления, описываемые уравнениями
Максвелла. Однако, согласно последним
(и это можно считать эмпирически
установленным, так как уравнения выведены
из эмпирически выявленных закономерностей),
скорость распространения света является
определённой величиной, не зависящей
от скорости источника (по крайней мере
в одной системе отсчёта). Принцип
относительности в таком случае говорит,
что она не должна зависеть от скорости
источника во всех ИСО в силу их
равноправности. А значит, она должна
быть постоянной во всех ИСО. В этом
заключается суть второго постулата:Постулат
2 (принцип
постоянства скорости света).
Скорость света в «покоящейся» системе
отсчёта не зависит от скорости источника.
Принцип постоянства скорости света
противоречит классической механике, а
конкретно - закону сложения скоростей.
При выводе последнего используется
только принцип относительности Галилея
и неявное допущение одинаковости времени
во всех ИСО. Таким образом, из справедливости
второго постулата следует, что время
должно бытьотносительным -
неодинаковым в разных ИСО. Необходимым
образом отсюда следует и то, что
"расстояния" также должны быть
относительны. В самом деле, если свет
проходит расстояние между двумя точками
за некоторое время, а в другой системе
- за другое время и притом с той же
скоростью, то отсюда непосредственно
следует, что и расстояние в этой системе
должно отличаться.Необходимо отметить,
что световые сигналы, вообще говоря, не
требуются при обосновании СТО. Хотя
неинвариантность уравнений Максвелла
относительно преобразований
Галилеяпривела
к построению СТО, последняя имеет более
общий характер и применима ко всем видам
взаимодействий и физических
процессов. Фундаментальная
константа ![]() ,
возникающая в преобразованиях
Лоренца,
имеет смысл предельной скорости
движения материальных тел. Численно
она совпадает со скоростью света, однако
этот факт, согласно современной квантовой
теории поля (уравнения которой изначально
строятся как релятивистски инвариантные)
связан с безмассовостью электромагнитных
полей. Даже если бы фотонимел
отличную от нуля массу, преобразования
Лоренца от
этого бы не изменились. Поэтому имеет
смысл различать фундаментальную
скорость
и
скорость света
,
возникающая в преобразованиях
Лоренца,
имеет смысл предельной скорости
движения материальных тел. Численно
она совпадает со скоростью света, однако
этот факт, согласно современной квантовой
теории поля (уравнения которой изначально
строятся как релятивистски инвариантные)
связан с безмассовостью электромагнитных
полей. Даже если бы фотонимел
отличную от нуля массу, преобразования
Лоренца от
этого бы не изменились. Поэтому имеет
смысл различать фундаментальную
скорость
и
скорость света ![]() [8].
Первая константа отражает общие свойства
пространства и времени, тогда как вторая
связана со свойствами конкретного взаимодействия.
[8].
Первая константа отражает общие свойства
пространства и времени, тогда как вторая
связана со свойствами конкретного взаимодействия.
В
связи с этим второй постулат следует
формулировать как существование
предельной (максимальной) скорости
движения. По
своей сути она должна быть одинаковой
во всех ИСО, хотя бы потому, что в противном
случае различные ИСО не будут равноправны,
что противоречит принципу относительности.
Более того, исходя из принципа
"минимальности" аксиом, можно
сформулировать второй постулат просто
как существование
некоторой скорости, одинаковой во всех
ИСО, а после
вывода соответствующих преобразований
- показать, что это предельная скорость
(потому, что подстановка в эти формулы
скоростей больше этой скорости приводит
к мнимости координат).
Относительность
одновременности
Если два
разнесённых в пространстве события
(например, вспышки света) происходят
одновременно в движущейся системе
отсчёта ![]() ,
то они будут неодновременны относительно
«неподвижной» системы S.
При
,
то они будут неодновременны относительно
«неподвижной» системы S.
При ![]() из
преобразований Лоренца следует
из
преобразований Лоренца следует ![]() Если
Если ![]() =
=![]() ,
то и
,
то и![]() =
=![]() .
Это означает, что, с точки зрения
неподвижного наблюдателя, левое событие
происходит раньше правого
.
Это означает, что, с точки зрения
неподвижного наблюдателя, левое событие
происходит раньше правого ![]() .
Относительность одновременности
приводит к невозможности синхронизации
часов в различных инерциальных системах
отсчёта во всём пространстве.
.
Относительность одновременности
приводит к невозможности синхронизации
часов в различных инерциальных системах
отсчёта во всём пространстве.
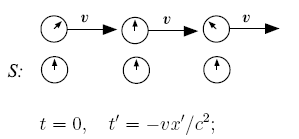 С
точки зрения системы S
С
точки зрения системы S
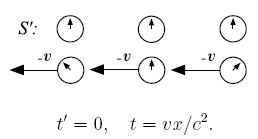 С
точки зрения системы S'
С
точки зрения системы S'
Пусть
в двух системах отсчёта вдоль оси x
расположены синхронизированные в каждой
системе часы, и в момент совпадения
«центральных» часов (на рисунке s)
они показывают одинаковое время.Левый
рисунок показывает, как эта ситуация
выглядит с точки зрения наблюдателя в
системе S. Часы в движущейся системе
отсчёта показывают различное время.
Находящиеся по ходу движения часы
отстают, а находящиеся против хода
движения опережают «центральные» часы.
Аналогична ситуация для наблюдателей
в S' ( рисунок).
Преобразования
Лоренца
Пусть координатные оси двух инерциальных
систем отсчёта S
и
параллельны
друг другу, (t,x,y,z) —
время и координаты некоторого события,
наблюдаемого относительно системы S,
а ![]() —
время и координаты того
же события
относительно системы
.
—
время и координаты того
же события
относительно системы
.
Общий
вид преобразований Лоренца в векторном
виде, когда скорость систем отсчёта
имеет произвольное направление: ![]() где
где  —
фактор Лоренца, r и
—
фактор Лоренца, r и ![]() —
радиус-векторы события относительно
систем S и S'.Если сориентировать
координатные оси по направлению
относительного движения инерциальных
систем (то есть в общие формулы подставить
—
радиус-векторы события относительно
систем S и S'.Если сориентировать
координатные оси по направлению
относительного движения инерциальных
систем (то есть в общие формулы подставить
![]() и выбрать это направление в качестве
оси x (то
есть так, чтобы система S' двигалась
равномерно и прямолинейно со
скоростью U относительно
S вдоль оси x),
то преобразования
Лоренца
примут следующий вид:
и выбрать это направление в качестве
оси x (то
есть так, чтобы система S' двигалась
равномерно и прямолинейно со
скоростью U относительно
S вдоль оси x),
то преобразования
Лоренца
примут следующий вид: 
![]()
![]()
![]() где C —
скорость света. При скоростях много
меньше скорости света (
где C —
скорость света. При скоростях много
меньше скорости света (![]() )
преобразования Лоренца переходят
в преобразования
Галилея:
)
преобразования Лоренца переходят
в преобразования
Галилея:
![]()
![]() Подобный
предельный переход является
отражением принципа
соответствия,
согласно которому более общая теория
(СТО) имеет своим предельным случаем
менее общую теорию (в данном
случае — классическую
механику).
Подобный
предельный переход является
отражением принципа
соответствия,
согласно которому более общая теория
(СТО) имеет своим предельным случаем
менее общую теорию (в данном
случае — классическую
механику).
