Работа внешних сил при вращении твердого тела

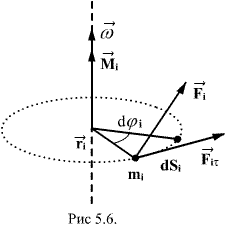Рассмотрим действие внешней силы  , приложенной к точке массой  . За время   элементарная масса   проходит путь   Работа силы   на этом пути определяется проекцией силы на направление перемещения, которая очевидно, равна тангенциальной составляющей   силы. Но   равна модулю момента   силы    относительно оси вращения. Работа  , и будет положительна, если   имеет такое же направление, как и   отрицательное, если направление векторов    и     противоположны. С учетом, что  

Работа всех сил, приложенных к телу Полная работа

11. Свободное вращение твердого тела. Момент инерции сложных тел. Понятие о степени свободы твердых тел. Вращение тела относительно свободной оси, относительно указанной точки. Гироскопический эффект. Прецессия гироскопа.

Момент инерции сложных тел Чайника -I= Полый цилиндр Пустой цилиндр Половина шара заполненная Большая половина шара заполненная Труба вращающаяся в центре Труба, вращающая с края Понятие о степени свободы твердых тел Числом степеней свободы твердого тела называется число независимых параметров, которые однозначно определяют положение тела в пространстве относительно рассматриваемой системы отсчета. Движение твердого тела во многом зависит от числа его степеней свободы. Свободное твёрдое тело в общем случае имеет 6 степеней свободы. Действительно, положение тела в пространстве относительно какой-либо системы отсчета, определяется заданием трех его точек, не  лежащие на одной прямой, и расстояния между точками в твердом теле остаются неизменными при любых его движениях. Согласно выше сказанному, число степеней свободы должно быть  равно  шести. Вращением твер­дого тела вокруг неподвижной оси называется такое движение, при котором все его точки, лежащие на некоторой прямой, называемой осью вращения, все время остаются неподвижными. Рассмотрим вращение твердого тела (рис.) вокруг оси, проходящей через две неподвижные точки O  и  . Проведем через ось    неподвижную полуплоскость   и движущуюся M вместе с телом полуплоскость _N. В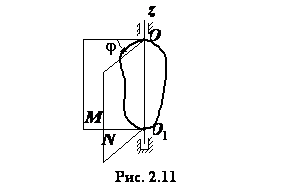 ращение тела будет определяться величиной дву­гранного угла    между по-луплоскостями _M  и _N. Угол    называется углом поворота. Условимся считать за положительное направление вращения тот случай, когда, смотря с заданного направления оси вращения, увеличение угла поворота наблюдается в сторону, противоположную движению часовой стрелки. При вращении угол поворота     изменяется в зависимости от времени. Равенство: является уравнением вращения тела вокруг неподвижной оси. Оно позволяет определить положение тела в любой момент времени. Угол    в равенстве выражается в радианах Вращение тела относительно указаной точки Название такого вида движения довольно точно его определяет. Часто это движение  называют сферическим движением потому, что все точки тела движутся по сферическим поверхностям.

Гироскопический эффект – это удержание (устойчивость) оси вращения объекта в пространстве. Этот эффект зависит от массы объекта, угловой скорости и от распределения моментов инерции. Если моменты инерции распределены немного неравномерно, то от этого будут возникать эффекты прецессии и нутации. Если моменты инерции распределены неравномерно, при этом ещё масса и угловая скорость объекта небольшие, тогда при эффекте прецессии ось объекта сначала описывает небольшую окружность, диаметр который всё время увеличивается. Затем ось объекта сама начинается вращаться в произвольных направлениях (кувыркаться). Прецессия гироскопа называется движение по окружности конца оси гироскопа относительно некоторой оси, сориентированной вдоль вектора внешней силы, происходящее под действием этой силы Наблюдать прецессию достаточно просто. Нужно запустить волчок и подождать, пока он начнёт замедляться. Первоначально ось вращения волчка вертикальна. Затем его верхняя точка постепенно опускается и движется по расходящейся спирали. Это и есть прецессия оси волчка. Главное свойство прецессии — безынерционность: как только сила, вызывающая прецессию волчка, пропадёт, прецессия прекратится, а волчок займёт неподвижное положение в пространстве. В примере с волчком этого не произойдет, поскольку в нём вызывающая прецессию сила — гравитация Земли — действует постоянно. Можно получить эффект прецессии, не дожидаясь замедления вращения волчка: толкните его ось (приложите силу) — начнётся прецессия. С прецессией напрямую связан другой эффект, показанный на иллюстрации ниже — это нутация — колебательные движения оси прецессирующего тела. Скорость прецессии и амплитуда нутации связаны со скоростью вращения тела (изменяя параметры прецессии и нутации в случае, если есть возможность приложить силу к оси вращающегося тела, можно изменить скорость его вращения).

12. Свободные гармонические колебания. Колебательное движение, условия необходимые для совершения колебаний. Уравнение гармонического колебания. Амплитуда, частота, период, фаза колебаний. Скорость и ускорение материальной точки при гармонических колебаниях. Дифференциальное уравнение гармонических колебаний. Колебательное движение, условия необходимые для совершения колебаний. вид неравномерного движения —колебательное. Колебательные движения широко распространены в окружаю­щей нас жизни. Примерами колебаний могут служить: движение иг­лы швейной машины, качелей, маятника часов, вагона на рессорах и многих других тел. Колебания бывают механические, электромагнитные, химические, термодинамические и различные другие. Несмотря на такое разнообразие, все они имеют между собой много общего и поэтому описываются одними и теми же уравнениями. Свободными колебаниями называются колебания, происходящие благодаря начальному запасу энергии, приданному колеблющемуся телу. Чтобы тело совершало свободные колебания, необходимо вывести его из состояния равновесия. Уравнение гармонического колебания устанавливает зависимость координаты тела от времени , x-координата колеблющегося тела, )-амплитуда колебания, -циклическая частота, t-время, -начальная фаза, =1м, =1м, , =1c, График косинуса в начальный момент имеет максимальное значение, а график синуса имеет в начальный момент нулевое значение. Если колебание начинаем исследовать из положения равновесия, то колебание будет повторять синусоиду. Если колебание начинаем рассматривать из положения максимального отклонения, то колебание опишет косинус. Или такое колебание можно описать формулой синуса с начальной фазой Амплитуда, частота, период, фаза колебаний Амплитуда - максимальное значение смещения или изменения переменной величины от среднего значения приколебательном или волновом движении. Неотрицательная скалярная величина, размерность которой совпадает с размерностью определяемой физической величины. Амплитуда — модуль максимального отклонения тела от положения равновесия. Амплитуда колебаний измеряется в единицах длины - метрах, сантиметрах и т. д. Чaстота́ — физическая величина, характеристика периодического процесса, равна количеству повторений или возникновения событий (процессов) в единицу времени. Рассчитывается, как отношение количества повторений или возникновения событий (процессов) к промежутку времени, за которое они совершены^]. Стандартные обозначения в формулах — ν, f или F. Единицей измерения частоты  является герц (русское обозначение: Гц; международное: Hz), названный в честь немецкого физика Генриха Герца. Частота обратно пропорциональна периоду колебаний: f = 1/T. Размерность Единица измерения Гц. Период колеба́ний — наименьший промежуток времени, за который осциллятор совершает одно полное колебание (то есть возвращается в то же состояние^[1], в котором он находился в первоначальный момент, выбранный произвольно). Обозначения: обычное стандартное обозначение периода колебаний: Т  Единицы измерения: секунда (с) Период колебаний связан соотношением взаимной обратности с  частотой: , Для волновых процессов период связан кроме того очевидным образом с длиной волны  , , где   - скорость распространения волны (точнее - фазовая скорость). Фаза колебаний — это величина, которая определяет положение колебательной системы в любой момент времени. Обозначается φ. Измеряется в радианах. Если колебания происходят по закону синуса и косинуса, т. е. при гармонических колебаниях, то фаза колебаний является аргументом функции cos (ωt +φ_o), где ω — циклическая частота колебаний, t — время, φ_o — начальная фаза колебаний, т. е. фаза в начальный момент времени. Скорость и ускорение материальной точки при гармонических колебаниях Скорость гармонического колебания Ускорение колеблющейся точки 

Уравнение гармонических колебаний можно записать в виде: x = A*sin(wt + f₀), где x - смещение точки от положения равновесия,A - амплитуда колебаний, (wt+f₀) - фаза колебаний, f₀ - начальная фаза, w - частота, t - время.

13.Пружинный, математический и физический маятник. Квазиупругая сила. Период колебаний пружинного, математического и физического маятников. Кинетическая и потенциальная энергия колебательной системы. Закон сохранения при колебательном движении. КВАЗИУПРУГАЯ СИЛА - направленная к центру О сила. модуль к-рой пропорционален расстоянию r от центра О до точки приложения силы (F=-cr), где с - постоянный коэф., численно равный силе, действующей на единице расстояния. К. с. является силой центральной и потенциальной с силовой ф-цией U=-0,5cr². Примерами К. с. служат силы упругости, возникающие при малых деформациях упругих тел (отсюда и сам термин "К. с."). Приближённо К. с. можно также считать касательную составляющую силы тяжести, действующей на матем. маятник при малых его отклонениях от вертикали. Для материальной точки, находящейся под действием К. с., центр О является положением её устойчивого равновесия. Выведенная из этого положения точка будет в зависимости от нач. условий или совершать около О прямолинейные гармонич. колебания, или описывать эллипс (в частности, окружность)

Колебания пружинного маятника В вертикальном положении на груз на пружине действуют сила тяжести и сила упругости пружины. Под действием силы тяжести пружина растягивается на х₁, а затем мы отклоняем его от этого положения на х.

Период колебаний   или   (формула Гюйгенса). Математи́ческий ма́ятник — осциллятор, представляющий собой механическую систему, состоящую из материальной точки, находящейся на невесомой нерастяжимой нити или на невесомом стержне в однородном поле сил тяготения^[1]. Период малых собственных колебаний математического маятника длины L неподвижно подвешенного в однородном поле тяжести с ускорением свободного падения g равен и не зависит  от амплитуды колебаний и массы маятника. Период колебаний физического маятника Период малых колебаний физического маятника Если амплитуда колебаний   мала, то корень в знаменателе эллиптического интеграла приближенно равен единице. Такой интеграл легко берется, и получается хорошо известная формула малых колебаний: .

Кинети́ческая эне́ргия ( ): В колебаниях любых систем происходит непрерывное превращение кинетической энергии в потенциальную и обратно. Кинетическая энергия системы, совершающей гармонические колебания, равна:   ,           

где скорость изменяется по гармоническому закону:  После подстановки, имеем:  Если учесть, что        и   ,  кинетическая энергиябудет равна:  Согласно формулам приведения:   , получим потенциальная энергия  ( ); Любая физическая система совершает гармонические колебания под действием квазиупругой силы, потенциальную энергию можно найти по формуле потенциальной энергии упруго-деформированного тела: т.к.   , то подставляя, получаем:  Т.к.     , то , тогда

 Если учесть, что      и       ,  потенциальная энергия будет равна:  

   

14. Затухающие колебания. Затухающие колебания. Дифференцированное уравнение затухающих колебаний и его решение. Период, декремент затухания, добротность колебания. Затухающие колебания — колебания, энергия которых уменьшается с течением времени. Бесконечно длящийся процесс вида   в природе невозможен. Свободные колебания любого осциллятора рано или поздно затухают и прекращаются. Поэтому на практике обычно имеют дело с затухающими колебаниями. Они характеризуются тем, что амплитуда колебаний A является убывающей функцией. Обычно затухание происходит под действием сил сопротивления среды, наиболее часто выражаемых линейной зависимостью от скорости колебаний   или её квадрата. Дифференцированное уравнение затухающих колебаний и его решение